Методы исследования в дипломной работе
Введение в дипломную работу обязательно содержит список использованных методов исследования. От их выбора зависит не только содержание работы, но и конечный результат. Правильный подбор методов помогает глубже изучить проблему и решить задачи.
Что такое методы исследования в дипломе
Метод — это подход автора к исследованию, способ продемонстрировать актуальность цели и пути ее достижения. Преподаватели и члены комиссии просят написать о методах в работе и рассказать на защите, что оценить глубину и аргументированность выводов. Изучение проблемы могут посчитать неполным, если анализ проведен на однообразных и непоказательных для данной проблемы исследованиях. Поэтому нужно оценить классификацию и выбрать подходящий вариант.

Правильно подобранные методы помогут сделать работу содержательной и значимой, наметить пути достижения цели и задач.
Какие бывают методы исследования в дипломной работе
Написание работы всегда опирается на результат анализа проблемы. Для его проведения выбирают один либо несколько методов, включенных в общую классификацию. Обоснование выбора зависит от темы и ее актуальности, поставленных задач, а также времени, отводимого для написания диплома. Значимыми считаются 3 группы:
- теоретическая;
- эмпирическая;
- статистическая.
Каждую из них подразделяют по направлениям работы. Иногда для формирования комплексного вывода необходимо использование нескольких методов. Тогда описание может носить комбинированный характер, содержать разнопрофильные выводы, давать аргументированные рекомендации. Особенно часто перекрещиваются теоретические и эмпирические методы.
Теоретические

Теоретический анализ — основа любого научного познания. С его помощью общий предмет исследования делят на мелкие направления. Среди них выделяют основной вектор, более значимый и важный. Именно на него направляют детальное изучение, чтобы раскрыть тему.
Теоретический метод может выглядеть в виде анализа, синтеза, объединения аналогичных свойств в группы (классификация), обобщения, моделирования, дедукции, индукции, проведения аналогий, абстрагирования, конкретизации, формализации. При этом дедукцию, индукцию, аналогию и абстрагирование относят к общефилософским методам. Для их применения важно умение правильно мыслить, выделять изучаемый предмет и, напротив, воспринимать его, как часть единого целого.
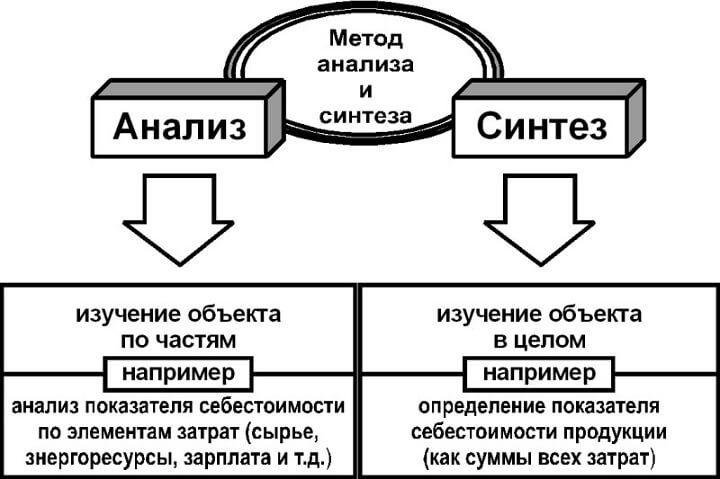
Синтез
Помогает продемонстрировать практический смысл исследования. Объект рассматривают как единое целое, характеристика которого обусловлена отдельными составляющими. Чтобы определить, какие из них стоит объединить, сначала лучше применить анализ.
К детализирующим подметодам синтеза относят:
- реорганизацию;
- автоматизацию;
- реинжиринг.
Продемонстрировать значение синтеза можно на следующих ситуациях:
- «Религиозная и светская жизненные позиции проявляются различным поведением и требуют особых подходов в воспитании. В то же время синтез понятий духовного становления личности обосновывает необходимость духовно-нравственной стороны общения с ребенком».
- «Все, что получено эмпирическим способом от различных органов чувств, разрозненно может не давать общей картины ухудшения или улучшения ситуации. Объединение этих «сигналов» воедино часто служит поводом к принятию оперативных мер».
Рассмотрение состояния здоровья населения не будет показательным, если затронуть только заболевания желудочно-кишечного тракта. Большую роль играют болезни сердца, суставов, нервов. Только проведя отдельные анализы по другим формам и обобщив полученные показатели, можно писать о проблеме общественного здоровья.
Анализ
Этот прием анализа применяют практически всегда. Он направлен на получение максимального количества доказательств целесообразности работы.

Анализ может предшествовать синтезу, определяя, какие характеристики нужно соединить. А может следовать за описанием проблемы, расчленяя ее на части и выводя закономерности каждой из них. В любом случае анализ поможет аргументировать выводы, почему тот или иной механизм приведет к достижению цели.
В качестве современной модели анализа рассмотрим SWOT. Это выявление и изучение слабых и сильных составляющих организации работы, например, с целью борьбы с падением производства. Матрица выглядит следующим образом:
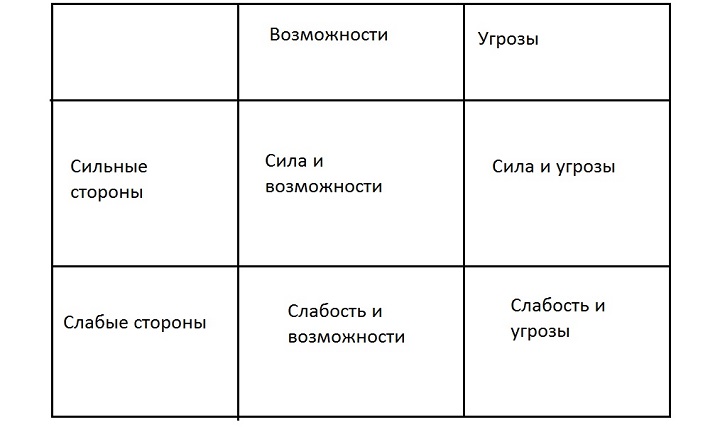
Анализ ситуации по двум направлениям (сильные и слабые стороны) позволит выявить моменты, на которые можно повлиять. SWOT-анализ — метод, при котором оценке подвергаются не только внутренние, но и внешние свойства. Его часто применяют при финансово-экономических проблемах.
В дипломной работе анализ бывает в виде рассуждений, целью которых является сравнение источников информации (гуманитарное направление) или описаний результатов, наблюдений (точные науки). Во втором случае возможно приведение цитат, данных из архивов.
Синтез и анализ неразрывно связаны друг с другом. Многие считают их этапами одного и того же теоретического раздела.
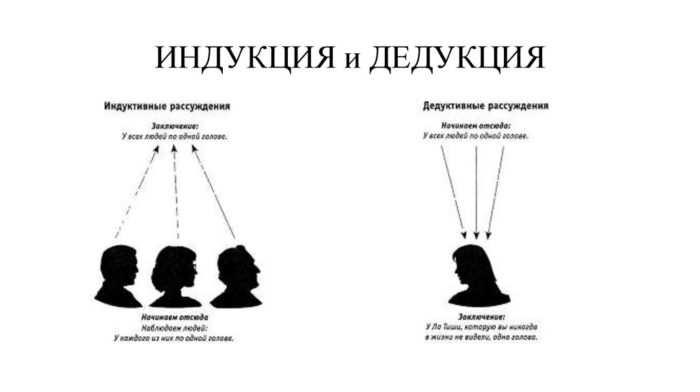
Дедукция
Когда дипломная работа предполагает наличие выводов о тех или иных событиях, явлениях, предметах, которые вытекают из многих мелких признаков, используется еще один способ обработки материала. Это дедукция.
Это составление схемы умозаключений, в результате которой от описания общего предмета познания приходят к нескольким частным.
Метод дедукции всегда рядом с индукцией. Эти два пути исследований часто взаимозависимы. Их применяют в комплексе.
Аналогия
Сравнение объекта исследования с другим. Автор исследования изучает их сходства и различия, сравнивает положительные и отрицательные черты. Проведение аналогии между субъектами позволяет выделить более значимые стороны их существования (или использования). Аналогии могут быть посвящены разделы исследования либо вся работа.

Ограничений в проведении аналогий не существует. Главное, чтобы сравнение было корректным. Проводить аналогию можно между:
- свойствами;
- отношениями;
- характеристиками;
- соответствием установленным стандартам;
- практическим применением;
- внешним видом и т.д.
В результате использования этого метода делается вывод о строгой аналогии, нестрогой и ложной.
Моделирование
Исследования в дипломной работе допускают перенесение реального объекта на созданную модель во время эксперимента. Объектом может быть материальный предмет, теоретическая ситуация, мысли, знаки. Метод используют в виде формул, чертежей, таблиц и т.д.
Пример сравнительной таблицы из дипломной работы:
В методиках проведения исследований можно встретить понятие «имитационного моделирования». Такой метод существует для математических моделей. Они имитируют функционирование объекта экономики или развитие экономических процессов за определенный отрезок времени. В основе лежит вероятностное значение заранее выбранных параметров. Целью такой работы является параметрическое изучение взаимовлияния процессов (или явлений) с возможным определением структурных закономерностей.
Для проведения математического моделирования заранее продумывают структуру эксперимента. Модели носят детерминированный либо стохастический характер. В первом случае это установление однозначного соответствия свойств модели и оригинала. Во втором — похожие черты случайны. Если модель подвержена влиянию большого количества факторов, ее свойства могут варьироваться.
Обобщение
Характеристика объекта на основании суммации типичных, присущих многим аналогичным единицам, свойств носит название обобщения. При этом редко встречающиеся признаки или случайные отступления исключают. Например, при подготовке работы по товароведческим дисциплинам обращаются к изучению потребительских свойств или тех показателей, которые можно отнести к идентифицирующим.

Обобщая, можно обратить внимание на многообразие объекта или типичные характеристики какого-либо процесса. Так, органолептика продуктов питания является основополагающей в их экспертизе.
Применяют обобщение двух вариантов: общее (любые абстрактные признаки) и закон (конкретно направленные). Другими словами, идти можно от фактов к их мысленному обобщению либо от мысли частной к глобальной. Следует помнить, что у мысленного обобщения есть предел. Остановка должна наступить тогда, когда затрагиваются философские области, не подвергающиеся обобщению.
К методу обобщения прибегают при составлении классификаций, проведении сравнительного анализа, желании идентификации признака либо действия.
Индукция
В переводе с латинского термин обозначает «наведение». Когда пишут диплом, часто проводится обобщение результатов исследования и экспериментов с целью рассуждения от единичного к целому. Индуктивные умозаключения характеризуются долей вероятности и относятся к опытным результатам и эмпирическим истинам.
Общепринято выделять несколько видов индуктивных разновидностей:
- полярная индукция;
- неполная;
- полная;
- научная.
Формализация
Дипломная работа, в которой применяется метод формализации, может быть не только в области математики. Сутью подхода является введение модели, на которую путем схем или формул передаются структура либо смысл происходящего.
Если материал нужно изложить лаконично, это оптимальный вариант. Формализация позволяет уйти от тяжелых, длинных конструкций, сделать прочтение комфортным не теряя смысловой цепочки.
Абстрагирование

Абстрагирование позволяет расширить проблему, взглянуть на нее с различных ракурсов. При этом изучаемый объект не привязывают к конкретной ситуации, времени, месту. Автор должен выбрать один аспект и рассмотреть именно его.
Организация раздела работы с использованием абстрагирования не так проста, как кажется на первый взгляд. Проблематичным является эмпирическое применение исследования. Поэтому применять его лучше в педагогике или психологии.
Классификация
В ряде случаев полезно использовать классификационную методологию. Классификация помогает выстроить четкую систему параметров, отобразить физические характеристики, жанры, стили и прочие единицы.
Например, рассмотрим одну из классификаций в дипломной работе по педагогике.
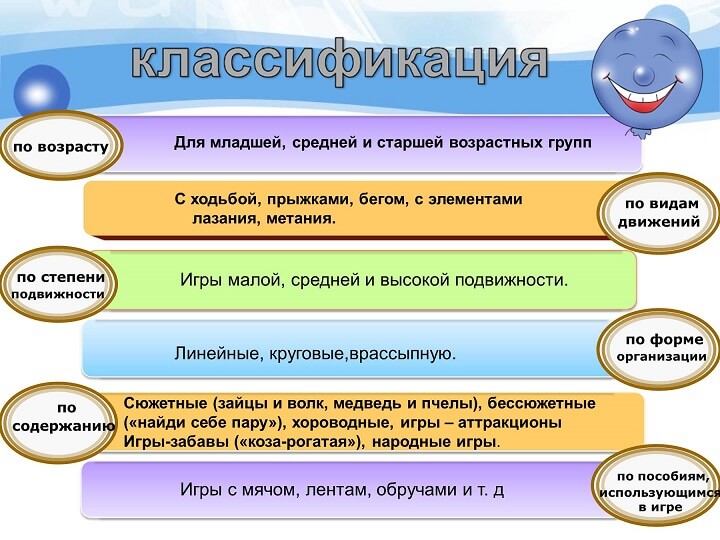
Отсюда видно, насколько полно и объективно автор изучил проблему, постарался охватить анализом широкий круг признаков.
Классификация нередко выгодна в экономических темах.
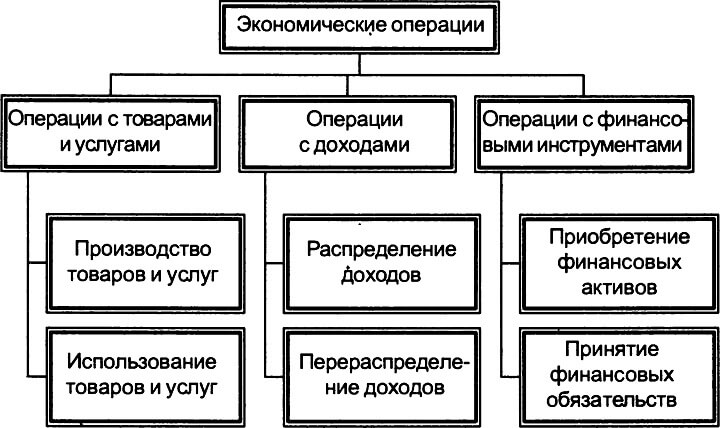
С ее помощью можно изложить раздел работы и сократить время устного изложения материала.
Конкретизация
Любой аналитический раздел можно дополнять уточнением характеристик фактора, предмета или явления. Обращаясь к конкретизации, автор работы подчеркивает важность выделенного фрагмента. Для конкретизации выбирается определенный момент. При этом абстракциям и общим характеристикам здесь не место. Важно, что состояние предмета исследуется в определенных условиях или на определенном этапе исторического развития.
Рассмотрим пример.

Конкретизация возможна, если реально запечатлеть именно тот момент, когда происходило изучение. Проводится она детально и целенаправленно.
Практические
Кроме теоретических, к общим методам исследований относятся практические (или частные). Их польза — в уникальном способе сбора данных, изучения и обработки информации. Применяют частные способы при необходимости установить закономерность, обосновать гипотезу, подтвердить целесообразность действия.
Сравнение
Сопоставлять можно 2, 3 или множество объектов, а также групп.
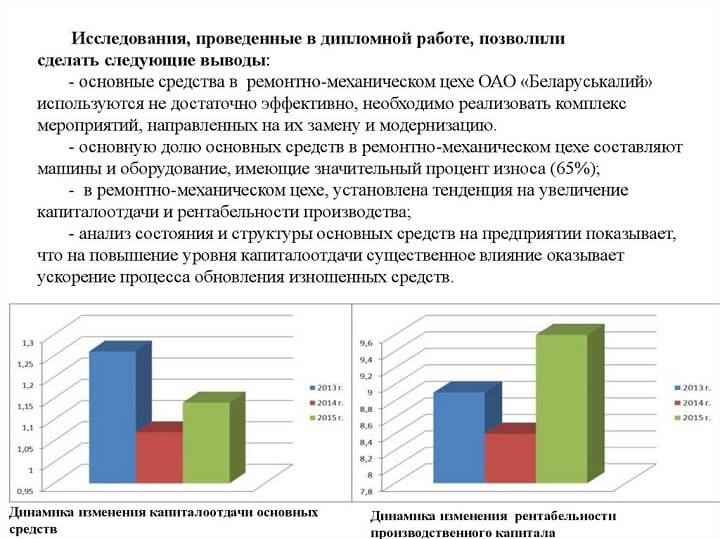
На примере показано сравнение показателей капиталоотдачи основных средств и рентабельности производственного капитала на 3 года. Графическое изображение сравниваемых показателей наглядно демонстрирует достижения и проблемы.
Ограничений для сравнения практически нет. Главное, чтобы единицы были равнозначными и достоверными. Результаты могут мотивировать к дальнейшему изучению либо навести на мысль о законченности эксперимента.
Наблюдение
Среди практических методов широко применяют наблюдение. Оно может сопровождаться фото- и видеосъемкой, быть основанным на психологических принципах, быть растянутым во времени либо включать определенный временной промежуток. Другими словами, это сбор сведений о свойствах, отношениях, показателях исследуемого объекта. Наблюдение практически всегда сопровождается анализом, сравнением, часто — последующей классификацией.
Измерение
Определение величины показателя проводится путем измерения. Метод относится к точным, поэтому его использование придает работе достоверность.
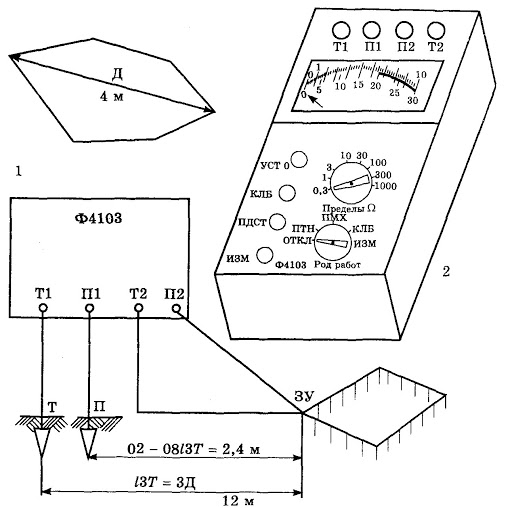
Например, в работе, посвященной измерениям сопротивления устройств с заземлением, такие схемы будут занимать лидирующие позиции. Измерения сочетают с теоретическими обобщениями, сравнением, моделированием. С его помощью делают выводы либо формулируют задачи.
В качестве примера рассмотрим проведение мониторинга атмосферного воздуха. Результаты динамического наблюдения с соответствующими замерами вынесены в таблицу.

Эксперимент
Для естественного эксперимента важны натуральные условия, констатирующего — первичная форма объекта, формирующего — реакция организма при влиянии извне.
Все виды экспериментов можно разделить на измерительные и квази. В первом случае предполагается наличие четких замеров, во втором — процесс происходит произвольно.

К проведению эксперимента необходимо быть готовым: составить программу, обеспечить оптимальную среду, подобрать оснащение, определить измерительные устройства.
В психологии работает термин «ложного эксперимента». Его участники получают установку на воздействие, при этом с ними ничего не происходит.
Также интересен мыслительный эксперимент. Автор рисует ситуацию в сознании. Такие методы используются, когда масштабы эксперимента велики и реальное его выполнение объективно затруднено.
Описание
В структуре работы описание может встречаться во введении, обосновании актуальности проблемы, обобщении результатов и выводов.

Описание — метод, присутствующий во всех дипломных работах. Это не только описание самого объекта изучения, но и характеристика материала, анализ данных, предложения для внедрения на практике.
Беседа и интервью
Беседа — мероприятие, при котором обязателен непосредственный контакт интервьюера и респондента. Интервью — это беседа по заранее составленному плану.
Оба варианта имеют «за» и «против». В первом случае возможно недопонимание вопросов, во втором — вариативность в формулировках.
Соединить два в одном можно с помощью полустандартизованного интервью, которое сегодня не является редкостью.
В психологических исследованиях практикуют групповые интервью, в ходе которых можно развивать несколько противоположных мнений. Важно, чтобы интервью не превращалось в опрос. Это совсем иной вид научного исследования.
К вопросам предъявляют требования, например:
- информативность;
- логичность;
- оригинальность;
- компетентность;
- понятность;
- однозначность и прочие.
Опрос и анкетирование
Представителями эмпирических методов являются опрос и анкетирование. Их особенностью является то, что полученная информация — не объективная реальность, а субъективные мнения людей. Результат анкетирования и опроса должен детально анализироваться или даже интерпретироваться.
Разновидность опроса — анкетирование. Это мероприятие, при котором выбранный контингент отвечает на заранее приготовленные вопросы. Обязательным условием выступают самостоятельные ответы. Кроме этого, опрос будет достоверным, если:
- Все участники были в одинаковых условиях.
- Личность экспериментатора всем неизвестна.
- Соблюдают добровольность, конфиденциальность, беспристрастность, отсутствие ущерба и другие.
Частные
Частные методы — второе название практических. Ориентировочный перечень приведен в таблице:
Социально-научные методологии
Методология социальных наук состоит из направлений:
- Эволюционизм. Изучение культурного развития общества на основании ее прогрессивного совершенствования и усложнения структур.
- Моделирование культурной динамики. По сути это изложение особенностей культур цивилизаций в их волновом или замкнутом проявлении.
- Структурный функционализм. Характеристика общественных культурно-исторических особенностей, которые призваны решить задачи в соответствии с потребностями людей.
- Структурализм. Метод, посвященный описанию исторических культурных объектов с позиции наличия взаимосвязи материального и морального аспектов.
- Пограничные методологии. Посвящены перспективному развитию культуры в историческом аспекте.
Гуманитарные методологии
К методам исследований в дипломной работе по гуманитарному направлению относят:
- исторический (описание в хронологии событий исторической важности);
- герменевтический (дешифровка первоначального смысла, заложенного в культурные явления при их задумке);
- феноменологический (описание исторических культурных событий по мере их явления, определение их смысла и актуальности);
- историко-психологический (изучение исторических смен в культуре у цивилизаций, обусловленных социальными изменениями и особенностями сознания);
- культурный символизм, постструктурализм (методология с признаками эклектики, которая объясняет суть контекстуально).
Как пишутся методы в дипломной работе
Описание методов, применяемых в дипломной работе, приводят в ее начале. Описать их можно следующим образом:

Краткое изложение — перечисление методов. Подробное позволит проверяющему оценить изученность проблемы. Однако такой способ обязывает автора хорошо разбираться в проблеме и в каждом методе.
Пример описания методов в дипломе

Правильно выбранный метод сделает дипломную работу содержательной, оригинальной, достоверной. Глубокое понимание сути позволит объединить разрозненные факты и проанализировать результаты. Помощь в выборе методов исследования можно получить на Феникс.Хелп. Специалисты расскажут, как составить план и выполнить задание.
Публикация научных статей студентов
О том, где и как студент может опубликовать научную статью, а также о всех нюансах ее оформления, рассказываем здесь.
Научная статья — итог деятельности ученых, студентов, аспирантов, магистров и тех, кто готовится к написанию диссертаций. В ней обобщаются результаты, которые были получены при работе над выбранной темой. Сделать эти результаты доступными для изучения коллег или просто интересующихся людей помогает публикация статей в специализированных либо ведомственных изданиях.
Для чего студенту публиковать научные статьи
Студенческие годы — время, когда человек определяется, насколько тот или иной академический предмет его интересует. Если у него появляется склонность заниматься наукой, полезным становится:
- изучение профильной литературы;
- ретроспективный анализ имеющихся материалов;
- организация и проведение лабораторных исследований;
- участие в групповых исследованиях на научную тематику.
Оформление результатов такой работы проводится путем написания и опубликования научной статьи. Исходя из принципа их написания, они подразделяются на научно-теоретические, обзорные, научно-практические.
К окончанию вуза студент может иметь достаточно широкий перечень публикаций, который в дальнейшем будет учитываться, например, при защите диссертации.
Отдельной строкой для студентов стоят экспериментальные статьи. Перед их написанием определяется цель изучения, методы работы и формулирование вывода. Публикации экспериментальных статей чаще бывают в студенческих изданиях, сборниках работ научной тематики. Они приурочиваются к значительным событиям, например, юбилейным датам или съездам ученых.
Публикации собственных научных наработок студенту необходимы для:
- Участия в семинарах, конференциях, особенно на зарубежном уровне.
- Поступления в магистратуру.
- Участия в конкурсах на получение государственных грандов.
- Включения в состав выступающих на профессиональных съездах молодых ученых.
- Наработки личного авторитета у профессорско-преподавательского состава.

Студент, ведущий активную научную деятельность, может претендовать по окончании вуза на место в аспирантуре, на профильной кафедре или в научной лаборатории. Количество опубликованных работ — значительный плюс к его резюме.
Правила написания научной статьи для публикации
Чтобы грамотно написать научную статью, над ней нужно поработать. Подготовка к написанию и сбор необходимой информации — половина гарантии ее качества.
Первым шагом должен быть выбор печатного издания и изучение его требований к публикациям. Они могут различаться по условиям оформления, перечню тем, объему, особенно в международных журналах. Затем определяются с темой и составляют план с выделением основных пунктов и подпунктов. Наличие хорошего плана научной статьи помогает грамотному, последовательному изложению материала, гарантирует, что не будет упущен ни один важный нюанс.

Следующий шаг — анализ имеющихся материалов, определение недостающих звеньев, чтобы итог был аргументированным и полноценным. Систематизируя имеющиеся сведения, часто автор считает необходимым изменить содержание того или иного раздела. В таком случае в план вносятся корректировки. Поднять значимость научной статьи можно, если просмотреть по этой теме новые разработки, публикации. Это подтвердит актуальность проблемы, придаст всему материалу современную направленность.
Когда план готов и обозначена структура, можно писать черновик.
Если пункты планы составлены корректно, в них заключен весь имеющийся материал, написание статьи не должно отнять много сил и времени.
Написанный черновик подлежит тщательному перечитыванию и внесению необходимых корректировок. Часто те, кто экономит свое время, в черновик вносит сокращенный текст, так называемый конспект своих мыслей. Тогда подготовка чистовика займет больше времени, поскольку потребует более полного изложения материала. Если в работе приводятся результаты собственных экспериментальных исследований, обязательно привести их название и основную характеристику.
Обязательное требование при написании научной статьи — изложение текста в научном стиле.

Для него характерны:
- целостное и связное изложение материала, обязательно законченное по смыслу;
- наличие достаточного фактажа;
- отсутствие эмоциональных составляющих;
- только литературное изложение, без уличной лексики и народных сокращений;
- разделение текста на абзацы, включение списков, подзаголовков;
- возможны цитаты.
Научный текст предполагает изложение материала понятным языком. Сложных предложений должно быть как можно меньше. Одно предложение — одна мысль. Применяемые специфические термины допускаются и даже приветствуются. Однако цель их употребления должна быть оправдана.
Текст должен быть логичен и точен по смыслу. Существуют требования к оформлению абзаца. Его первое предложение должно быть вступительным либо задавать вопрос, ответ на который раскрывается далее. Завершается абзац кратким выводом.
Выбирать способ изложения материала следует ориентируясь на предполагаемую аудиторию читателей. Это определяют при ознакомлении с правилами издания, в котором планируется публиковать.
Требования к оформлению по ГОСТ
Правильно оформить научную статью не менее важно, чем ее написать. Иначе ее не удастся отправить для публикации в авторитетные издания. Среди обязательных требований к оформлению следующие:
- Статья должна иметь классификационный индекс, который можно получить на сайте ИИЦ Научной библиотеки.
- Название прописывается на двух языках: русском, английском. Сокращения, как и точка, не используются. Шрифт — жирный, расположение — центровое.
Пользоваться онлайн-переводчиками — значит не исключать ошибки в переводе, особенно для текстов, содержащих научные термины.
- После названия следует аннотация, для которой так же обязательно исполнение на русском и английском языках. Ее длина — 150–300 слов.
- Для поисковых систем в научной работе обязательно указание ключевых слов. Их должно быть не менее десяти, на двух языках.
- Аббревиатуры объясняются по тексту один раз, в том месте, где они применяются впервые.
- Присутствующие таблицы, рисунки, графики должны иметь сквозную нумерацию и обязательно поясняться в тексте.
Обязательными разделами являются также обзор используемой литературы, список источников, а также основная часть, содержащая выводы.
Подробные требования по оформлению научной статьи изложены в ГОСТ.

Исходя из норматива, содержание статьи должно уместиться на 5-10 страницах, напечатанных Times New Roman14. Поля — 2 см, междустрочный интервал — 1,5. Графические материалы располагаются на альбомном листе. Ссылки на них в тексте обязательны.
Редакторы изданий могут вводить дополнительные требования, например, проверку текста на антиплагиат и прочие.
Пример научной статьи для публикации
Чтобы визуально представить, как должна выглядеть правильно оформленная научная статья, достаточно иметь перед глазами образец.

Источник: upload-c8e18b222bbc1d0ef2dd63c6098129a0.commondatastorage.googleapis.com
Что делать после написания
Закончив написание научной статьи, необходимо начать подготовку к ее публикации.

На этом этапе не должно возникнуть трудностей, поскольку перед написанием студент получал сведения от конкретного издания о требованиях к работам.
Журналы для публикации
Публикациями студенческих научных статей занимаются многие издания, в том числе международного уровня. Издательство «Интернаука» выпускает «Студенческий вестник» и «Научный журнал». Предлагают напечатать студенческие научные работы научный журнал «Студенческий форум», научно-образовательское издание «Образование и наука в России и за рубежом».
ВАК рекомендует печатать научные статьи в изданиях с проверенным авторитетом. Те, кто хочет заручиться поддержкой комиссии, могут зайти на ее сайт, ввести шифр специальности (или ее группы) и выбрать среди предлагаемых журналов подходящий вариант.
Международные
Чтобы подобрать для публикации журнал международного уровня, достаточно зайти на один из сайтов: Scopus, Elsevier, Science direct.
Для такого уровня публикации нужно быть уверенным в качестве перевода, а также быть готовым, что процесс может стать трудоемким и недешевым.
Легче напечататься в изданиях участникам и победителям международных конкурсов, викторин, олимпиад. Объявления об их проведении можно найти на специализированных сайтах.
Электронные
Научный журнал «Студенческий», зарегистрированный Роскомнадзором, печатает статьи бесплатно в электронном варианте, в формате pdf. При этом можно получить электронный сертификат, свидетельствующий о публикации в журнале.
Многие сегодня пользуются для публикации своих научных работ научной электронной библиотекой eLIBRARY.ru. Ее пользователи — студенты, аспиранты, магистранты не только РФ, но и других стран. На ресурсе eLIBRARY.ru публикуются также материалы конференции «Молодой исследователь» - мероприятия, обеспечивающего перспективный уровень обмена информацией между участниками.

Претендующие на участие в конференции должны подать заявку и прикрепить к ней свою научную статью. После публикации автор получает сведения об ISSN, УДК, ББК своей работы, а также доступ к электронному сборнику.
Где еще можно публиковать научные статьи
Студенты могут обратиться по вопросу публикации своих научных статей в следующие издательства:
- Российский аналитический журнал «Скопус»;
- «Студенческий научный журнал»;
- Профильные журналы, типа «Вопросы медицины», «Современные философские взгляды», «Актуальные вопросы социологии и психологии».
Кроме того, многие вузы выпускают свои литературные издания. Пример: «Вестник Томского государственного университета», «Известия Российского государственного педагогического университета им. А.И.Герцена» и другие.
Сколько стоит публикация
Цены на публикацию научных студенческих статей разнятся в зависимости от индивидуальных требований изданий. Так, в «Студенческом форуме» за одну страницу нужно заплатить 95 рублей. В «Международном научно-исследовательском журнале» за каждые 1500 знаков — 400 руб, а один графический материал оценивается в 50 руб.
Elibrary.ru предлагают также условия бесплатной публикации для тех, у кого 1000 и более цитирований и не менее 90% уникальности статьи.
Авторам, обращающимся за публикацией повторно, электронное издание предлагает скидку 10% от общей цены, а льготные категории могут рассчитывать на 20%.
Бесплатная публикация статей
Студенты редко расположены тратить деньги на публикации статей. Это снижает возможность заявить о себе научной общественности, уменьшает бонусы для поступления в аспирантуру, защиту кандидатской диссертации и т.д. Если средства не позволяют, можно напечатать работу бесплатно следующими способами:
- Попросить взять руководство над собой и своей статьей известного ученого. Их работы многие журналы печатают бесплатно для поднятия рейтинга.
- Записаться в очередь на публикацию. Внося незначительную плату за продвижение этой очереди, можно дождаться самой публикации бесплатно.
- Принимать участие в научных конкурсах, объявляемых онлайн, победителям которых дается право напечататься бесплатно.
Некоторые издания периодически объявляют набор в печать статей бесплатно, например, журнал научных публикаций «Скиф. Вопросы студенческой науки».
Срочная публикация научной статьи
ВАК не рекомендует пользоваться услугами печатных изданий, которые гарантируют публикацию за два дня. Специалисты аргументируют такой подход невозможностью провести полноценное рецензирование. Однако, если все-таки желательно это сделать срочно, нужно собрать максимум информации о выбранном издании.
Примером издательства, предлагающего срочную публикацию, является «Проблемы науки». Для журнала этот срок составит 5 дней, журнала ВАК — 15, в зарубежных изданиях SCORPUS — 1,5 месяца. «Интернаука» предлагает напечатать научную статью в журналах РИНЦ за период до 24 часов, ВАК - от трех дней.
Необходимость срочной публикации указывается в сопроводительном письме с объяснением причин оперативности.
Внеочередностью публикации иногда удостаиваются участники конференций, которые проводят соответствующие издания. Информацию об их проведении, включая международный уровень, размещают на информационных сайтах.
Если научная статья написана, а заниматься ее публикацией нет времени или желания, на помощь придут профессионалы Феникс.Хелп. Здесь вам грамотно и быстро прорецензируют готовую работу, внеся полезные коррективы.
Решение задач на силу упругости
Любое тело перестает падать вниз, если его подвесить на крепкий шнурок. На него по-прежнему действует сила тяжести. Но она уравновешивается еще одной величиной – силой упругости шнурка. Как она действует на тело, что нужно для ее преодоления, — вопросы, ответы на которые найдете в материале.
Что такое сила упругости
Любое тело, совершающее заданный полет, в конце концов падает на землю под действием собственной силы тяжести. Исключение составляют предметы, подвешенные кверху либо располагающиеся на опоре. Их падение становится невозможным, поскольку силу тяжести компенсирует упругость подвеса. Опытным путем еще в школьной программе демонстрируется момент: когда две силы равны, предмет «замирает» в воздухе. При этом их направления действия строго противоположны. Явление, препятствующее падению подвешенных либо размещенных на опоре предметов, обусловлено проявлением силы упругости.
Сила упругости — сила, возникающая в теле при его деформации и стремящаяся вернуть его в прежнее состояние.
Чем сильнее растягивается нить, на которой подвешен предмет, и чем больше прогибается доска под грузом, тем значительнее сила упругости, которая в них возникает.
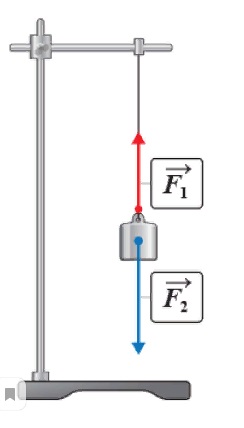
Нить стремится растягиваться до тех пор, пока две величины не уравновесятся.
Растяжение нити аналогично, например, следующим явлениям:
- изменению формы мяча при ударе по нему ногой (начинает действовать сила сжатия);
- противостоянию каната при закручивании его вокруг своей оси (сила кручения);
- сдвиганию частей одного предмета друг относительно друга (сила сдвига);
- сложностям согнуть прут в дугу или окружность (сила кручения).
Во всех случаях внешней силе, действующей в определенном направлении, начинает препятствовать другая величина, направленная противоположно и стремящаяся компенсировать ее абсолютное значение.
К такому выводу впервые пришел английский ученый Роберт Гук в 1660 году, отметив, что интенсивность изменения длины тел при их растягивании прямо пропорционально зависит от значения силы упругости.
Его открытие приобрело статус закона Гука, формула которого выглядит следующим образом:
\(Fупр=k*Δl\)
\(k\) – коэффициент пропорциональности, имеющий специальное название «жесткость»;
\(Δl\) – величина, характеризующая изменение длины тела.
K зависит от свойств материала изготовления тела, его параметров и форм.
В физике закон Гука может применяться только для незначительных деформаций. Если наступает этап, когда предел пропорциональности превышен, взаимосвязь напряжения и изменения формы теряет свою линейность. Существуют среды, для которых закон Гука не работает.
Выражение закона Гука возможно и через другую формулу:
\(\xi\;=\;x⁄l\)
где \(\xi\;\) — относительная деформация,
\(\sigma=F⁄S\)
где \(\sigma\) — напряжение, возникающее в материале,
\(S\) — площадь поперечного сечения тела,
\(\varepsilon=1⁄E\sigma\)
Коэффициент жесткости и модель Юнга имеют существенное различие: если первый зависит от материала, формы и размеров тела, то второй — только от свойств материала.
В каких условиях применяется закон Гука
Универсальным вариантом для применения закона Гука является тонкий стержень. \(F\) в данном случае выражает ту силу, которая к нему прилагается. Зависит она от разницы длины до и после воздействия, а также коэффициента упругости материала.
\(F=k\ast\Delta l\)
Как было сказано выше, \(k\) зависит от качества материала и габаритов. Выражая названую зависимость через площадь сечения и длину, формула для коэффициента получает следующий вид: \(F=ES/L\). Буквой \(Е\) здесь обозначается все тот же модуль Юнга – механические свойства материала. Далее следует ввести понятия относительного удлинения:
\(\xi=\Delta l/L\)
и напряжения в поперечном сечении:
\(\sigma=F/S\)
Конечная формула закона Гука может выглядеть и так:
\(\triangle l=FL/ES\)
Для понимания того, какие условия необходимы для функционирования закона Гука, достаточно рассмотреть два понятия: среда и сила. В таких средах, как газы, жидкости, особенно вязкие, механические особенности процессов упругости не действуют. В то же время даже очень интенсивная сила не будет работать в ряде сред.
Обязательные условия для ее проявления:
- Незначительные изменения формы.
- Достаточная упругость материала.
- В материале ни при каком воздействии не происходит изменений линейного характера.
Рассмотрим график, отражающий зависимости:
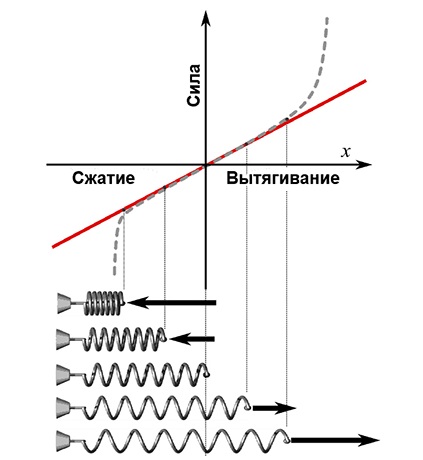
Нижний левый квадрат демонстрирует линейную зависимость при не интенсивных растяжениях. Затем пунктирная линия демонстрирует потерю этой «линейности». Визуально это проявляется «непослушанием» пружины: она перестает принимать свой первоначальный вид при интенсивном растяжении. Если его вовсе не прекращать, может нарушиться природная структура материала, произойдет полный излом.
Аналогичная картина наблюдается при процессе сжатия. В правом верхнем квадрате отражены следующие особенности:
При небольшом сжатии – связь прямая (красная линия).
При увеличении силы зависимость теряет «линейность» — см. пунктир.
Сильное сжатие заставляет пружину нагреваться, она теряет первичные свойства. Происходит слипание витков и разрушение структуры материала.
Примеры решения задач на силу упругости
Задания по определению силы упругости часто встречаются в экзаменационных работах и олимпиадах.
Задача 1
Для растяжения пружины прикладывают силу 30 Н (F1). Тогда ее длина составляет 28 см. При ее сжатии с такой же F2, длина уменьшается до 22 см. Найти начальную длину пружины, а также коэффициент ее жесткости.
Решать задачу следует по схеме:
\(F1=k(l1-l0)\)
\(F2=k(l0-l2)\)
Из этих формул вытекает: \(l1-l0=l0-l2\)
\(l0=(l1+l2)/2=(28+22)/2=25\)
Определение жесткости пружины нужно произвести по формуле:
\(k=F1/(l1-l0)=30/(28-25)*10^{-2 }=1000\)
Ответ: 25 см, 1000 Н/м
Задача 2
Пружины соединены способом, изображенным на схеме:
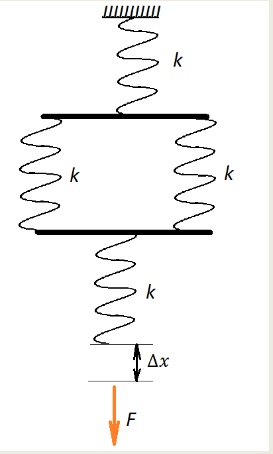
Жесткость каждой составляет 10 Н/м. Определить величину силы, которую нужно приложить ко всей системе, чтобы точка ее приложения стала ниже на 10 см.
Решение происходит по этапам:
1. Растяжение верхней и нижней пружин характеризуются формулой:
\(\triangle x2=F/k\)
2. Поскольку средние пружины подсоединены параллельно, их растяжение происходит в соответствии с формулой:
\(\triangle x2=F/2k\)
Каждая из пружин при этом растянется на: \(\triangle x1/2\)
Следовательно, справедливо математическое выражение: \(\triangle x2=\triangle x1/2\)
Через промежуточные формулы:
\(2,5\triangle x1=\triangle x\)
\(\triangle x1=\triangle x/2,5\)
\(10/2,5=4\)
находим конечную формулу для решения задачи:
\(F=k\triangle x1=10\ast0,04=0,4\)
Ответ: сила равна 0,4 Н.
Задача 3
Один из тренажеров в спортивном зале высотой 2 м состоит из двух пружин, которые закреплены на потолке. Их длина одинакова (40 см), а жесткости обозначены k1, k2. При приложении к одной из пружин силы 360 Н (в точке А), нижняя ее часть пружина опустится до самого пола. Потянув в точке В и приложив силу 240 Н, коснется пола сама эта точка. Какова жесткость пружин?
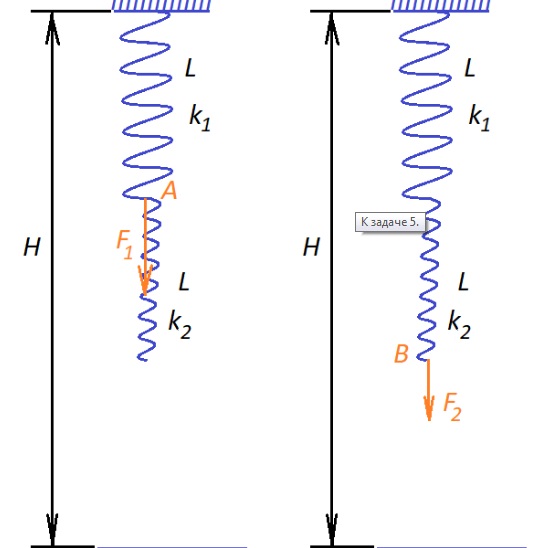
Прикладывая усилия к точке А, вызываем растяжение только пружины сверху. Когда ее длина достигнет 1,6 м, нижняя коснется пола. Таким образом, верхняя удлинилась на 1,2 м.
\(L+\triangle l1=H-L\)
\(\triangle l1=H-2L=1,2\)
\(k1=F1/\triangle l1=360/1,2=300\)
Относительно точки В действуют формулы:
\(F2/k1+F2/k2=H-2L\)
\(240/300+240/k2=1,2\)
Значит \(k2=240/0.4=600\)
Ответ: коэффициенты пружин будут равны 300 и 600 Н/м.
Задача 4
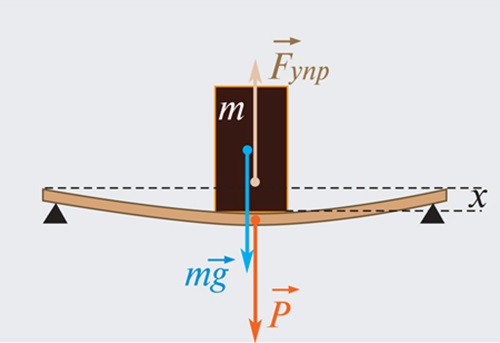
Пружина массой 5 кг прикреплена к бруску, который лежит неподвижно на поверхности. Как изменится сила ее натяжения, если угол наклона будет увеличиваться от 30о до 60о?
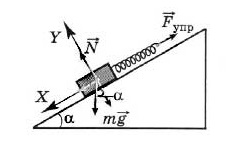
Как видно из рисунка, брусок испытывает влияние трех сил: тяжести, натяжения пружины, реакции опоры.
Для равновесия бруска необходимо равенство величин:\(mg=Fупр=N=0\)
Откладывая величины на осях координат, выходим на формулы:
\(mg\sin\alpha-\;\;Fупр=0\)
\(N\;-\;mg\;\cos\alpha\;=\;0\)
Из первого уравнения следует:
\(Fупр=m\ast g\ast\sin\alpha\)
Учитывая, что угол наклона поверхности, на которой расположен брусок, меняется, ΔFyпp можно определить по формуле:
\(\Delta Fyпp\;=\;mg(\sin\alpha2\;-\;\sin\alpha1)\;\)
Подставляя в формулу значения, высчитывают значение искомой силы:
ΔFyпp=5 * 10 * (0,866 - 0,5) = 18,3 Н
Те, кому нужна практическая или теоретическая помощь в освоении темы по силе упругости, могут обратиться на Феникс.Хелп. Вам всегда помогут.
Задачи по физике на тему «механика» с решением
Все движущиеся тела подчиняются законам механики. Не составляет исключение параллельное взаимодействие с другими телами, а также изменение их положения во времени и пространстве.
Что такое механика, какие области охватывает
Механика — раздел физики, изучающий движение материальных тел, их равновесие и взаимодействие с соседними телами.
Существует теоретическая сторона, которая затрагивает общие закономерности движения, включая планеты солнечной системы, а также характеристики полета, и дисциплины, изучающие частные моменты работы двигателей, механизмов, машин и их внутренних частей.
Исходя из этого, сформулировать предмет механики можно следующим образом:
- теоретическая сторона;
- механика сплошных сред;
- специальные разделы, такие как: механизмы и машины, гидравлические процессы, механика почв и т.п.
Почему возникла необходимость дифференциации на разделы? В ее основе лежат свойства времени, материи и нахождения в пространстве. Опираясь на такие характеристики, механика подразделяется на виды:
- классическую;
- релятивистскую;
- квантовую.
Изучая механические системы с учетом их степеней свобод, проводится обобщение импульсов и, при необходимости, наложение их на систему координат. Сама механическая система может являться замкнутой (изолированной от окружающих факторов) и незамкнутой (открытой). Вторая классификация оценивает характеристику во времени: статические и динамические. К динамическим системам, к примеру, относят математический, физический и крутильный маятники, твердое тело, неголономную систему, сплошную среду и др.
Общий курс школьной программы включает такие разделы, как механика, динамика, статика, кинематика. Решаются задачи в этих ключах, а также на законы сохранения.
Примеры решения задач по теоретической механике
Задача 1. Путь автомобиля (\(S\)) условно разделен на три части: первую, вторую и третью. Какой будет средняя скорость его движения на первой части (\(V_1\)), если средняя скорость (\(V\)) равна 37,5 км/ч, а скорость на второй и третьей частях пути (\(V_2\)) была равна 50 км/ч?
Решение:
Обозначим время, затраченное на первой трети пути \(t_1\), на оставшихся двух третях — \(t_2\).Тогда:
\(t_1+t_2=S\div3V_1+2S\div3V_2\)
\(t_1+t_2=S\div V\)
\(V_1=VV_2\div(3V_2-2V)=\)25 км/ч
Задача 2. Моторная лодка за 3 часа переплывает по реке из точки А в точку Б. На возвращение она тратит 5 часов. Зная, что скорость движения лодки одинаково туда и обратно, определите, сколько времени займет движение из точки А в точку Б у плота.
Если скорость теплохода \(V_1\), а течения — \(V_2\), то время, затраченное на весь путь от А до Б, составляет:
\(t_1=S\div(V_1+V_2)\).
Путь от Б до А лодка прошла за:
\( t_2=S\div(V_1-V_2).\)
Выразим \(S\) через \(t\) и \(V\), приравняв математические выражения пути через эти категории:
\(t_1(V_1+V_2)=t_2(V_1-V_2)\).
Применив стандартные действия сложения, получаем:
\(V_1=4V_2\)
В итоге отмечаем, что лодка без учета скорости течения пройдет путь за 4 часа. Ее скорость, когда она плывет против течения, в 3 раза превышает скорость реки.
Ответ: плот сможет преодолеть расстояние от А до Б за 15 часов.
Задача 3. Мужчина едет в поезде со скоростью 80 км/ч. Навстречу идет товарный поезд со скоростью 40 км/ч. Длина встречного состава — 1 км. На протяжение какого времени мужчина будет наблюдать из окна за движущимся встречным поездом?
Решение задачи можно провести двумя методами.
Метод 1. Если относительно Земли мужчина находился в точке с координатой \(Х=О\), то окончание товарного поезда было от него удалено на 1 км (\(Х_т=1\)км). Координата первой точки \(Х\) находится на расстоянии, определяемом по формуле \(V_1t\), второй — \(Х_т-V_2t\).
Когда хвост встречного поезда был на уровне мужчины-пассажира, \(Х_1=Х_2\) или \(V_1t=X_тt–V_2t\).
Отсюда \(t=X_T\div(V_1+V_2)\)
Метод 2. Если рассматривать положение мужчины относительно товарного поезда, его скорость будет равна \(V_0=V_1+V_2\). Учитывая, что длина поезда 1000 м, мимо мужчины будут следовать его вагоны в течение времени:
\(t=l\div(V_1+V_2)\)
Подставив значение, получаем, что \(t=20\) сек.
Задача 4. Тело подвесили на полуметровой нити. Она невесома и нерастяжима. Требуется определить минимальную скорость в горизонтальном направлении, которую надо сообщить телу, чтобы оно совершило полный оборот по вертикальной плоскости.
Алгоритм решения следующий. Согласно закону сохранения энергии для тела, переходящего из нижнего положения в верхнее, характерно:
\(M{V_0}^2\div2=mg+2L+MV^2\div2\) (\(L\) — длина нити).
Когда тело находится вверху, на него воздействуют силы тяжести и натяжения нити. Они суммарно передают ему центростремительное ускорение, которое направлено вниз — в направлении точки подвеса:
\(Mа_ц=Mg+T\)
По условию задачи тело должно достичь верхней точки, следовательно, \(Т=0\). Поэтому:
\(MV^2\div l=Mg\), откуда \(V^2=gl\).
Подставляем выражения друг в друга и получаем:
\(M{V_0}^2\div2=2Mgl+Mgl\div2\)
\({V_0}²=g4l+gl=5gl\)
\(V_0=\surd(5\ast10\ast0,5)\)=5 (м/с)
Примечание. При условии расположения тела на жестком стержне, вверху скорость тела будет равна 0. При этом
\(M {V_0}^2\div2=Mg2l\), отсюда
\( {V_0}^2=4gl\)
\(V_0=\surd(4gl)=2\surd(gl)\)
Подставив значения, получаем ответ задачи.
\(V_0=2\ast\surd(10\ast0,5)\)=4,47(м/с)
Задача 5. При катании на роликах два человека взялись за разные концы одной веревки. При движении один из них получает ускорение. Каково ускорение второго катающегося, если он весит в 1,5 раза меньше? Силу трения между землей и поверхностью роликов в расчет не брать.
По материалам задачи понятно, что на катающихся действуют три силы:
- сила тяжести, измеряемая формулами m1g и m2g;
- реакция опоры N1 и N2;
- натяжение веревки между ними: T1 и T2.
Кроме того, катающиеся перекладывают друг на друга собственные силы, которые согласно третьему закону Ньютона равны по значениям, т.е. T1=T2=T. Направления этих сил указаны на рисунке.
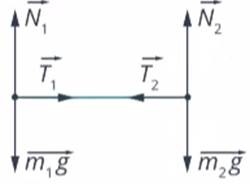
Катающиеся получают ускорение, охарактеризовать которое можно по второму закону Ньютона. Поскольку между ними отсутствует жесткое соединение, эти значения могут отличаться.
Примечание. В объяснении к задаче следует учесть, что силу, с которой катающийся тянет веревку, не учитываем, поскольку задача направлена на анализ обратно направленной силы.
Решение:
По второму закону Ньютона, для каждого тела характерно:
m1g+N1+T1=m1a
m2g+N2+T2=m2a
Проведя проекции на ось Y, получается:
m1g-N1=0
m2g-N2=0
При проекции на ось Х:
T1=m1a1
-T2=-m2a2
Если T1=T2=T, m1=1,5m2 (по условию задачи), то
T=1,5m2a1
T=m2a2
Проводя математические действия, выводим конечную формулу: a2=1,5a1
Ответ задачи: ускорение одного из катающихся в 1,5 раз больше, чем другого.
Задача 6. Обосновать расчетами, отличается ли сила тяжести, направленная на 2 литра воды от нее же, направленной на 2 литра ртути.
Формула силы тяжести: F=mg
Найти массу по формуле: \(m=\rho V\),
где ρ-плотность вещества, а V — его объем.
Выводим итоговую формулу и, зная плотность и объем обоих веществ, подставляем значения:
\(F_1=\rho_1{V_1}g \)
\(F_2=\rho_2V_2 g\)
Тогда \(F_1\div F_2=\rho_1V_1 g\div\rho_2 V_2 g\)
Отсюда \(F_1\div F_2=\rho_1V_1 \div\rho_2 V_2 \)
Находим табличные данные: ρ1=1000 кг/м3; ρ2=13540 кг/м3
Таким образом \(F_1\div F_2\)=0,07
Задача 7. Нужно определить показания механического динамометра, когда к нему будет подвешена гиря массой 0,8 кг. Каков в таком случае ее вес?
Весом называется сила, действующая на опору или нить, на которой висит предмет.
Поэтому: P=F=mg
Считая g=10 м/c2, проводим вычисления:
P=F=0,8*10=8 Н
Задача 8. Зная, что возле поверхности Земли \(g=9,81\)м/с2, необходимо определить величину ускорения на высоте \(3R_z\).
Формула ускорения свободного падения, с учетом Закона всемирного тяготения, выглядит так:
\(g=GM\div R^2\)
\(R\) — расстояние от тела до центра Земли.
Зная, что \(R=R_z\), корректируем формулу:
\(g=GM\div Rz^2\)
G=6,67*1011H*м2 кг-2
Поскольку R=3Rz
\(g=G\ast M\div Rz^2\)
\(g_2=G\ast M\div(3Rz)^2\)
\(g_2\div g=GM\div(3Rz)^2\div (GM\div R_z^2)=1/9\)
\(g_2=g\div9=1,09\) м/c2
Быстро и грамотно решить задачи на тему «Механика» помогут на сайте Феникс.Хелп. Обращайтесь, если катастрофически не хватает времени или вы не уверены в правильности собственных рассуждений. За решениями задержки не будет — здесь знают свое дело!
Куда можно поступить с обществознанием
По окончании школы в выборе учебного заведения руководствуются собственными соображениями, а также выбранными предметами во время ЕГЭ. Для тех, кто сдавал экзамен по обществознанию, открыты возможности поступления по гуманитарному направлению. При этом перечень специальностей лучше заранее проанализировать.
Что изучает обществознание
Иногда приходится слышать, что обществознание — предмет, который необходим для поступления на юридические факультеты. Знать особенности развития общества значит правильно оценивать права и свободы его членов. На практике это более широкое понятие, предполагающее анализ многих общественных наук. Наиболее значимыми из них являются:
- философия;
- социология;
- правоведение;
- политология;
- психология, в большей степени — социальная;
- экономика и другие.
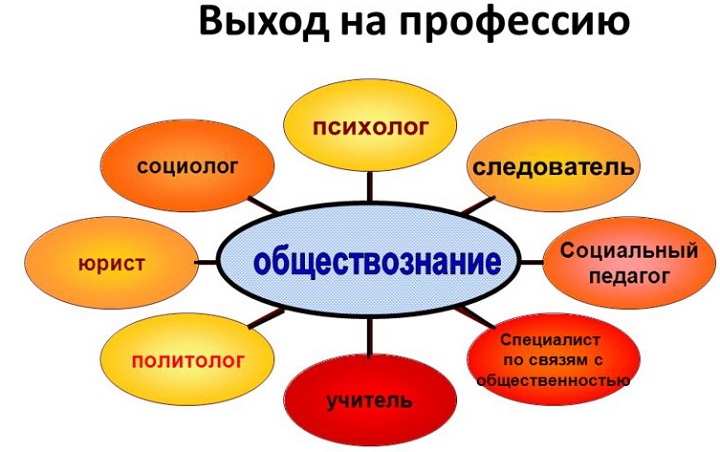
Для получения полной характеристики общества, необходимо дать оценку вопросам, решаемым в экономической, политический, духовной, социальной сферах. Эти направления в обществознании важны в комплексе.
Перечень специальностей, предполагающих экзамен по обществознанию, довольно значителен.
Обществоведение в качестве профильного предмета часто рассматривается при поступлении на направления: международные отношения, история, археология, логистика, социология, социальная работа, туризм, политология, психология, журналистика, гостиничное дело, философия и религия, физкультура и спорт, культурология, юриспруденция. Эти направления объединены необходимостью знаний законов общественной жизни, изучением места и роли человека в обществе.
Обучаясь по названным направлениям, можно получить много различных профессий, которые в корне отличаются друг от друга.
Например, если пойти по направлению социальной работы, можно получить такие современные специальности, как демограф или медиатор социальных конфликтов. Направление педагогики дает возможность специализации по проектированию индивидуальных образовательных траекторий, цифровому кураторству. С маркетингом связаны специальности форсайтера, маркетолога-аналитика, специалиста по рекламе.
Предоставить результаты ЕГЭ по обществознанию понадобится и тем, кто желает получить специальность, связанную с управлением и менеджментом, а также с управлением персоналом. Особенностями современных авторитетных компаний являются присутствие в их штатах менеджеров по персоналу, по развитию, по внутренним коммуникациям и т.д.
Как сдается ЕГЭ по обществознанию
Не секрет, что выбор обществознания для ЕГЭ часто основывается на кажущейся простоте предмета: даже не зная конкретного ответа на вопрос, можно путем своей эрудиции заработать приличный бал. Уровень общей эрудиции действительно важен. Но для предмета «обществоведение» необходимо понимание политологии, юриспруденции, социологии, истории и литературы.
Разобраться в законах развития общества трудно, если руководствоваться только логикой и строить догадки. Чтобы, получая специальность, стать поистине профессионалом, необходимо освоить школьные программы и развить гуманитарную эрудицию.
Структура экзаменационной работы по обществознанию охватывает различные области подготовки. Она состоит из двух частей. В первой — 20, во второй — 9 заданий. На выполнение всей работы отводится 3 часа 55 минут. Максимальное количество первичных баллов — 65, в т.ч. 35 баллов можно получить за первую часть и 30 — за вторую.
Предлагаемые вопросы охватывают 5 тематических блоков: философия (человек и общество), экономика, социология, политология, право.
На какие специальности можно поступить с обществознанием
Выбор специальности может происходить до написания ЕГЭ или после него. В первом случае будущий абитуриент узнает заранее о профилирующих предметах в конкретном вузе. Во втором случае экзамен выбирается на основе личных предпочтений. В таком случае, имея на руках результаты ЕГЭ, абитуриент выбирает, в какой вуз их подать. Второй вариант считается неправильным, поскольку выбором руководит не увлеченность профессией, а желание выбрать более легкий путь, чтобы поступать.
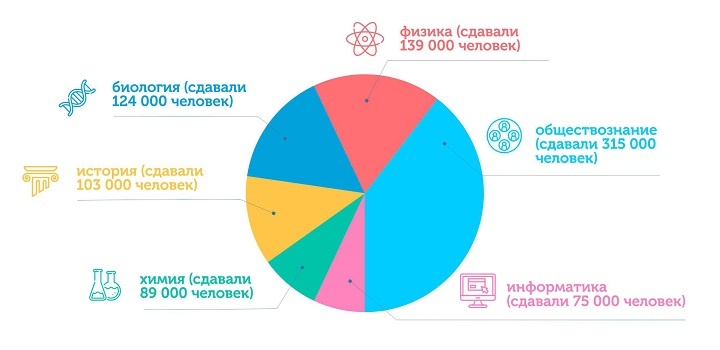
Не секрет, что часто экзамен по обществознанию выбирается именно по этой причине. На рисунке показана доля выпускников, выбравших его для ЕГЭ по данным Рособрнадзора.
Занимаясь изучением обществознания, школьник познает законы развития общества, его духовные составляющие, а также социально-экономические характеристики в одном предмете. Получая специальность в университетах, студенты должны быть готовы к разделению обществознания на ветви, которые вместе образуют гуманитарный профиль.
Условно его можно разделить на группы:
- Филология и педагогические дисциплины (в т.ч. русский и английский языки, история, география, информатика, физика и другие).
- История, юриспруденция, философия, политология, культурология.
- Психология, биология.
Кроме этого, обществоведение является одним из обязательных, но не профилирующих экзаменов на экономические специальности:
- экономика;
- менеджмент;
- сервис;
- торговое дело.
Такие факультеты с математическим уклоном лучше выбирать тем, у кого склонность учиться точным наукам.
Более подробный перечень направлений, для поступления на которые необходим результат ЕГЭ по обществознанию, следующий:
- радиоэлектронные системы и комплексы;
- клиническая психология;
- психология служебной деятельности;
- экономическая безопасность;
- таможенное дело;
- правовое обеспечение национальной безопасности;
- правоохранительная деятельность;
- судебная экспертиза;
- перевод;
- актерское искусство;
- литературное творчество;
- монументально-декоративное искусство;
- живопись;
- графика;
- философия;
- история;
- социология;
- туризм и другие.
Самые востребованные
Знания законов, по которым происходит развитие общества в целом и по отдельным направлениям, необходимо для получения многих специальностей. С учетом высокой ступени социального сознания и значительного уровня протекающих в мире процессов наиболее востребованными сегодня специальностями являются:
- юриспруденция;
- журналистика;
- таможенное дело;
- правоохранительная деятельность;
- маркетинг;
- политология;
- психология;
- гостиничное дело;
- логистика.
Часть из них можно приобрести в колледже (техникуме) после 9-ти лет обучения в школе. Более высокий уровень подготовки требует наличия ЕГЭ после 11-го класса.
В какие ВУЗы можно поступить после 11 класса
Выпускники 11-х классов, имеющие при себе результат ЕГЭ по обществознанию, могут поступить в ряд российских университетов, в которых такой тест является профильным. Для примера это:
- Московский государственном университете им.М.В.Ломоносова (msu.ru);
- Московский педагогический государственный университет (mpgu.su);
- Уральский государственный педагогический университет (uspu.ru);
- Государственный академический университет гуманитарных наук (gaugn.ru);
- Санкт-Петербургский государственный экономический университет (unecon.ru),
А также прочие Московские, Санкт-Петербургские, Екатеринбургские, Тульские и прочие университеты.
Абитуриенты, имеющие высокий балл, чаще пытаются поступить в Москву и Санкт-Петербург. Многих привлекают Казань, Томск, Новосибирск.
Куда поступить с обществознанием после 9 класса
Когда жизненные планы связаны с поступлением после 9-го класса и экзаменом по обществознанию, нужно приготовиться сдавать ОГЭ. Это 4 экзамена, из которых математика и русский — обязательные, обществознание (по выбранному профилю) и один нужно довыбрать.
Несмотря на имеющиеся на руках результаты ОГЭ, основой для поступления является балл аттестата. Это особенно полезно тем, кто интересуется специальностью, связанной с географией или обществознанием, но имеющий ОГЭ по прочим дисциплинам.
Одна из востребованных специальностей такого профиля — гостиничный сервис. Поступив после 9-го класса, для ее получения нужно проучиться очно три года, по завершении присваивается квалификация менеджера, портье, администратора отеля.
Еще один пример — дошкольное образование. Учиться нужно четыре года, после чего можно работать воспитателем или руководителем детских кружков и секций.
Востребованы сегодня специалисты по профилю «реклама». Маркетологи и менеджеры по рекламе, девелоперы, промоутеры и другие специалисты, занимающиеся разработками маркетинговых стратегий и созданием рекламной продукции, — настоящие и будущие двигатели мировой экономики.
Лучшими колледжами, производящими подготовку по специальностям с ОГЭ по обществознанию, сегодня являются:
- Гуманитарный колледж РГГУ (gumcollege.rggu.ru);
- Государственное бюджетное профессиональное образовательное учреждение города Москвы «Московский колледж управления, гостиничного бизнеса и информационных технологий "Царицыно"» (collegetsaritsyno.mskobr.ru);
- Красногорский государственный колледж (krstc.ru);
- Санкт-Петербургский технический колледж управления и коммерции (tcmc.spb.ru);
- Политехнический колледж городского хозяйства (pkgh.edu.ru) и многие другие.
Выбирая профессию с необходимыми знаниями по обществознанию, абитуриент и будущий специалист получают огромные возможности для личностного развития, самосовершенствования, карьерного роста.
Успешный результат ЕГЭ по обществознанию — широкий круг возможностей для получения востребованной интересной профессии. Чтобы экзамен прошел успешно, а выбор будущей профессии был удачным, вы можете обратиться за помощью на сервис Феникс.Хелп. Их профессиональные консультации и практические советы — залог успешной вступительной компании, даже если ее подготовка ограничена по времени.
