Решение задач по статистике в колледже

Проведение любого вида анализа, как оперативного, так и ретроспективного, требует грамотного использования статистических приемов. Они помогают оценить наличие достоверной связи между явлениями, выводят усредненные показатели, которые важны для факторной оценки.

Особенности решения задач по статистике в колледжах и вузах

На современном этапе развития общества применение методов статистической обработки материала позволяет:

• проанализировать те или иные явления, определив характер и выявив закономерности;
• спрогнозировать ситуацию на близкую либо отдаленную перспективу;
• спланировать перечень мероприятий для корректировки выявленной тенденции.

Статистика применяется в экономике, здравоохранении, педагогическом анализе, бизнесе, социальных науках и общественных явлениях.

В учебных программах колледжей и вузов обязательно присутствует курс статистики, целью которого является научить студентов статистической методологии, правилам применения статистических выводов в практической деятельности специалиста.

Статистика является целостной системой, затрагивающей как социально-экономическое, так и отраслевое направление, часто имеет международный характер.

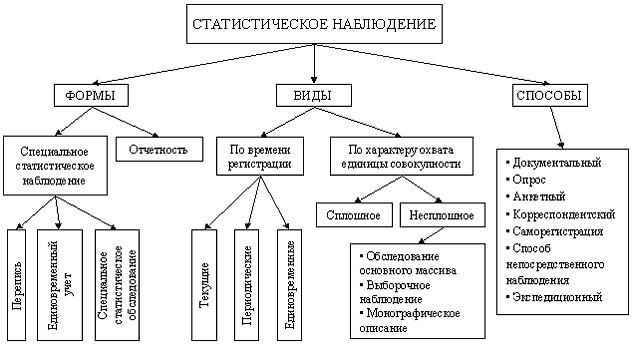
Решение задач по статистике в учебных заведениях среднего и высшего звена опирается на утвержденные алгоритмы, смыслом которых является четкое следование оговоренным этапам.

1. Сбор данных. При этом в работу берутся не все показатели. Исключение составляют, например, годы, когда действовали факторы непреодолимой силы (стихийные бедствия, эпидемии и т.п.). Таким образом, формируются выборки показателей, каждая из которых предназначена для определенной статистической обработки.
2. Обобщение выбранных данных – преподаватель дает студенту характеристику существующих методов и способов получения показательного результата, выведения закономерностей и подтверждения их графически.
3. Анализ. Устанавливаются связи между явлениями или факторами, наблюдается наличие взаимосвязи между количественными и качественными показателями.
4. Итог. Определение динамики того или иного процесса, характеристика демографических процессов среди населения либо прочих анализируемых факторов.

Формируя определенную совокупность для статистической обработки, обращают внимание на частоту встречаемости того или иного признака или варианта. Тот из них, который встречается чаще других, статистически обозначает «моду». Благодаря ему формируется обобщающая характеристики величины признака. Обозначается мода Мо. При рассмотрении дискретного ряда (т.е. ряда, образованного числами) мода выделяет то значение, которое встречается чаще остальных.

Существует еще одна характеристика выстроенного динамического ряда. Это медиана. Она находится в середине вариационного ряда, построенного по принципу возрастания или убывания, и делит его на две половины.

Мода и медиана в математике называются распределительными средними. Их основное назначение сводится к формированию общей характеристики выбранного варьирующего признака какой-то величины.

Методы расчета ошибки выборки 

Задачи со статистическими методами решений имеют в своей основе генеральную совокупность. Под этим термином понимается суммарное количество предметов наблюдения, которые имеют тот или иной общий признак.

Пример

Населенный пункт можно охарактеризовать численностью населения, количеством имеющихся на территории промышленных предприятий, учреждений образования, здравоохранения и т.д.

Выбрав нужный признак, его характеристики отбираются и объединяются в выборку (выборочную совокупность). Однако необходимо помнить, что для обеспечения полноценного действия полученного в результате анализа вывода, каждая выборка должна быть репрезентативной.

Кроме репрезентативности, каждая выборка может иметь ошибку. Ошибка выборки может возникнуть по причине недостаточного количества ее размера. Другими словами, в изучаемом процессе недостаточный доверительный интервал.

Ошибки можно дифференцировать на:

• статистическую;
• систематическую.

Именно статистическая определяется размером выборки. С увеличением числа наблюдений она уменьшается.

Систематическая ошибка не математического характера. Она зависит от воздействия определенных факторов, которые могут сместить результаты наблюдения в ту или иную нетипичную сторону.

В математике, когда говорят об ошибке выборки, имеют ввиду статистическую.

Рассмотрим расчет ошибки выборки для обобщения результатов опроса респондентов. Обычно такие социальные исследования носят выборочный характер, т.е. опрашиваются не 100% людей, а некоторая часть. Именно поэтому нельзя быть уверенным в полученном результате на 100%.

Определить ошибку выборки можно по следующим формулам:

1. \(\Delta=Ζ\surd(p\times g\div n)\)

Она применяется для тех ситуаций, когда размер выборки намного меньше чем сама генеральная совокупность.

 2. Для случаев с незначительной разницей между объемом выборки и генеральной совокупностью рекомендуется формула:

\(\Delta=Ζ\surd(p\times q\div n\times((N-n)\div(N-1))\)

Условные обозначения:

Δ - предельная ошибка

Ζ - коэффициент доверительного уровня

N - величина генеральной совокупности

n - объем выборки

p - часть опрошенных, у которых есть исследуемый признак

q = 1−p - те опрошенные, которые не имеют исследуемого признака

Статистическая сводка и группировка

После этапа статистического наблюдения следует составление статистической сводки. Его цель – систематизация имеющейся информации, составление общей характеристики для рассматриваемой совокупности.

Дифференцируют простую и сложную сводку. При простой в качестве результата анализа имеют общие итоги. При сложной – итоги в виде анализов по группам, возможно, объединенных в таблицы.

Основными этапами составления сводки являются:

• отбор признака, по которому будет проводиться группировка;
• обозначение последовательности, которая ляжет в основу формирования каждой группы;
• определение системы показателей, которые будут статистически характеризовать каждую группу и совокупность;
• составление таблиц с целью наглядной демонстрации полученных результатов. 

Метод статистической обработки путем группировки применяется, когда вся исследуемая генеральная совокупность может быть разделена на группы по выбранному признаку. Этот признак называется группировочным. 

Таким образом, группировка – это один из способов выделения в совокупности данных, характеризующих выбранный признак. Такое изучение имеет своей целью изучить структуру совокупности, выявить возможную взаимосвязь между изучаемыми признаками. Например, применяя группировку, легко выделить в большой организации участки с высоким выполнением запланированных показателей.

В экономической отрасли группировка применяется если нужно проанализировать трудовые ресурсы, наличие средств труда, материальные ресурсы и т.п.

Сегодня выделяют следующие виды группировок:

• простая;
• сложная;
• типологическая;
• структурная;
• аналитическая и др.

При структурной группировке могут исследоваться состав и структура имеющегося статистического материала. При аналитической – исследуются связи, возникающие между отдельными элементами и их группами. В таких случаях могут выделяться обобщающие значения, результативные или те, которые определенным образом влияют на обобщающие.

Ряды распределения и статистические таблицы

При проведении статистического анализа пользуются построением рядов распределения. Их целью является определение самых характерных признаков и присутствующих закономерностей, действующих в совокупности. Вид рядов распределения определяется тем, какой признак лежит в основе группировки. Принимая за основу качественные показатели, получают атрибутивные группировки. Делая акцент на количественном признаке, ряд называется вариационным. В свою очередь, вариационный ряд может быть ранжированным, дискретным, интервальным.

В ранжированном ряду элементы совокупности располагаются в порядке возрастания или убывания. Так легко выявить наибольшее либо наименьшее значения. В дискретном ряду присутствует признак прерывающихся изменений. Он может выглядеть двухграфной таблицей, в которой одна графа – признак, вторая – частота его встречаемости.

Если анализируемый признак претерпевает постоянные изменения, строится интервальный вариационный ряд. В таком случае в графе для количественных показателей указывается не одно значение, а интервал от и до.

Типовые примеры с решениями и выводами для студентов

К типовым задачам по статистике в программах колледжей и вузов относятся:

1. Определение моды динамического ряда.

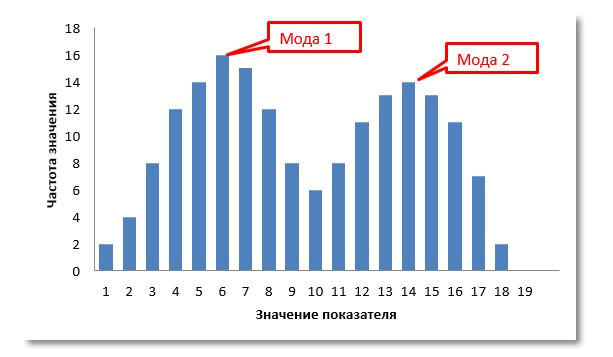
В динамическом ряду 1, 5, 6, 4, 8, 4, 3, 4, 9 найти моду. Так как число 4 встречается чаще других, оно и является модой. Легко определить моду с помощью гистограммы.

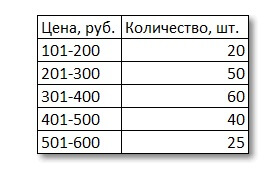
При интервальных данных задача решается чуть труднее. Допустим, даны исходные материалы:

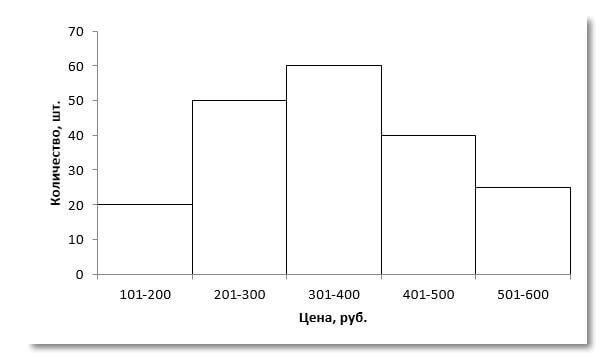
На графике модальный интервал с наибольшей частотой – 301-400 (самый высокий столбик).

Моду рассчитываем по формуле:

\(Mo=Xo+h(ƒMo-ƒMo-1)\div((ƒMo-ƒMo-1)+(ƒMo-ƒMo1)\)

где M_o-мода

X_o- начало модального интервала

h - Размер модального интервала

ƒ – частота модального интервала

ƒM_o-1 – частота интервала перед модальным

ƒ M_o– частота интервала после модального

В результате расчета для данного примера Мода равна 334,3 руб

Задача № 2

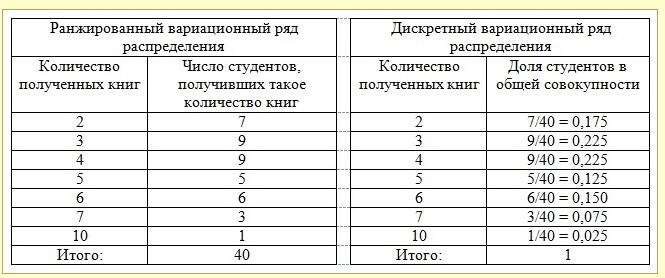
Студенческой библиотекой пользуются 40 человек. Было выписано, сколько книг взял за год каждый из них. Получился результат:

Строим ранжированный и дискретный вариационные ряды в таблице:

Построению таблицы предшествовало обозначение элементов ряда. Полученная совокупность содержит в себе много вариантов для анализа, как пользуются студенты библиотечным фондом.

Статистика – дисциплина, позволяющая на результатах конкретного анализа выявить наиболее проблемные либо успешные организационные моменты и провести коррекцию того или иного типового направления работы. Если нужна помощь с учебными заданиями по статистике, обращайтесь в ФениксХелп.