Классическая механика на практике: 4 задачи с ответами
Предлагаем вашему вниманию 4 примера задач и рассказываем, как их решить.
Задача 1. Вращательное движение
На маховике радиусом 0,2 м на максимальном удалении от центра вращения находится точка А. Маховик вращается по закону у = Аt3 + Вt2 + C. При этом величина А = 1 рад/с3 , В = 3 рад/с2, С = 5 рад. Время с начала движения равно 2 с. Определите полное ускорение точки и среднюю угловую скорость вращения этого маховика за время с начала движения.
Решение:
Так как в условии задачи дан закон вращения маховика, то для того чтобы найти угловую скорость, мы можем продифференцировать его выражение относительно переменной «t».
Получим:
Или:
ω = (Аt3 + Вt2 + C)1 = 3Аt2 + 2Вt.
Таким же образом мы можем найти угловое ускорение:
Или:
ℇ = (3Аt2 + 2Вt)1 = 6Аt + 2В.
Теперь вспомним, как находить полное ускорение точки, если нам известны «ω» и «ℇ»:
где:
и V = ωR = > аN = ω2R; а аT = R2ℇ.
Тогда получаем:
Подставим в это выражение полученные выше значения «ω» и «ℇ»:
Тогда для t = 2 c получим полное ускорение точки:
и среднюю угловую скорость вращения:
Ответ: а = 115,2 м/с2 , ω = 15 рад.
Задача 2. Второй закон Ньютона и сила трения
Поезд двигался со скоростью 36 км/ч. Масса поезда — 4000 т. Затем поезд начал торможение и проехал за 60 секунд 510 метров. Какова сила трения, подействовавшая на поезд при торможении?
Решение:
По второму закону Ньютона равнодействующая сил, действовавших на поезд во время торможения, равна:
F = ma.
При этом единственной силой, действовавшей на поезд в направлении движения, является сила трения. Поэтому запишем:
ma = Fтр.
Чтобы найти силу трения, действовавшую на поезд, необходимо найти ускорение «а». Считая силу трения постоянной, делаем вывод, что движение при торможении является равнозамедленным. Тогда ускорение мы можем найти, используя формулу для нахождения пути при равнозамедленном движении:
Откуда получаем:
Тогда получаем:
Подставим числовые значения:
Ответ: 2• 105 Н.
Задача 3. Закон сохранения импульса
Для очистки металлических деталей от ржавчины в некоторых случаях применяют пескоструйную установку. При этом струя песка направляется на обрабатываемую поверхность под некоторым углом. Наиболее оптимальным углом при ударе песчинок о деталь является 45°. Определите величину импульса, которой обладает система «обрабатываемая деталь — песчинка» при скорости струи, равной 10 м/с, в результате удара одной песчинки массой 0,01 г.
Решение:
Для решения задачи используем закон сохранения импульса. В общем случае мы запишем:
Р1 = – Р2,
Где:
Р1 — импульс, которым обладает песчинка при ударе о деталь;
Р2 — импульс, который сообщает поверхность детали песчинке при отскоке.
При этом:
Р = mV1;
Р = mV2,
где:
m — масса песчинки;
V1 — скорость песчинки при ударе;
V2 — скорость песчинки при отскоке от детали.
Для удобства расчетов примем допущение, что:
V1 = V2 = V.
Тогда получаем:
mV1 = – mV2;
mV1 + mV2 = 0;
mV + mV = 0;
2mV = 0.
Тогда суммарный импульс, которым обладает система «обрабатываемая деталь — песчинка», будет равен:
ΣР = 2mV.
Поскольку направление струи составляет 45°, то при расчетах необходимо использовать проекцию вектора импульса на ось ОХ. Тогда выражение примет вид:
ΣР = 2mV•cosα.
Подставим числовые значения:
ΣР = 2•0,00001•10•cos 45° = 0,00014 = 1,4•10-4 кг•м/с.
Ответ: 1,4•10-4 кг•м/с.
Задача 4. Движение по окружности
Летчик на спортивном самолете выполняет фигуру высшего пилотажа «мертвая петля». При этом его самолет совершает движение по круговой траектории в вертикальной плоскости. Определите силу давления летчика на сидение в нижней точке, если линейная скорость в этот момент равна 10 м/с. Масса летчика — 60 кг. Радиус круговой траектории равен 25 м.
Решение:
Согласно третьему закону Ньютона сила давления летчика на сидение равна по модулю и обратна по знаку силе реакции опоры со стороны сидения.
По второму закону Ньютона равнодействующая всех сил, действующая на человека в нижней точке траектории вращения, будет равна сумме этих сил, направленных в противоположные стороны. Можем записать:
ma = P – N,
где:
N — сила реакции опоры;
P — вес тела.
При этом:
N = mg.
Тогда:
P = ma + mg = m (a + g).
Величину центростремительного ускорения «а» найдем по формуле:
где:
V2 — линейная скорость движения тела по окружности;
R — радиус вращения тела.
Тогда:
Подставим числовые значения:
Ответ: 840 Н.
Надеемся, с образцами решений типовых задач по классической механике выполнение домашнего задания станет проще. А если у вас все еще остались вопросы или задача не похожа ни на одну из приведенных нами, обращайтесь за помощью к специалистам ФениксХэлп. Поможем, расскажем и объясним, как правильно решить.
Понравилась статья?
Подпишитесь на наш блог и получайте наши статьи первым!
Или подписывайтесь на нас в соцсетях:
Заметили ошибку? Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так

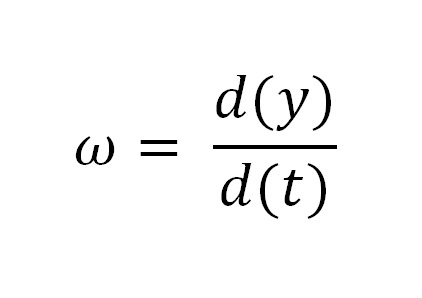
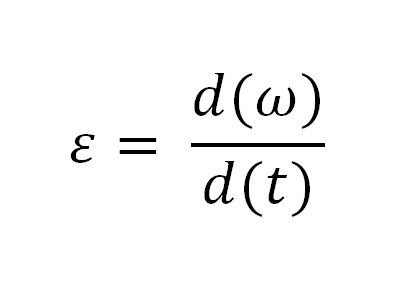
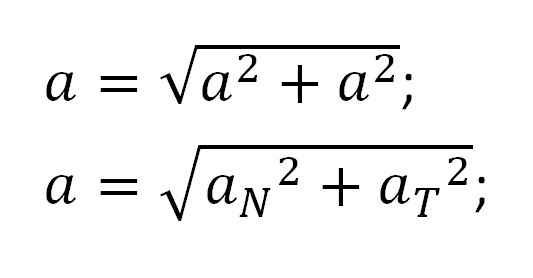
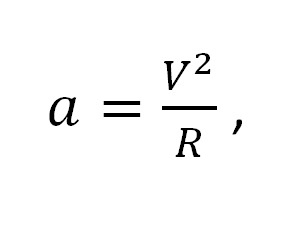
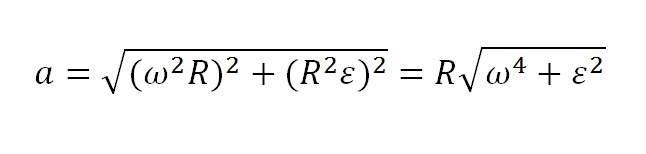
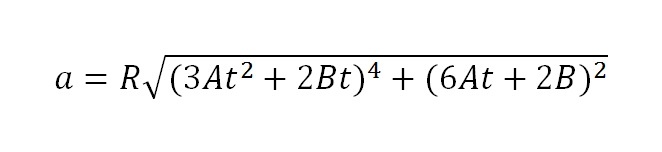
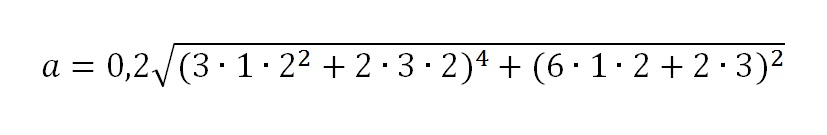
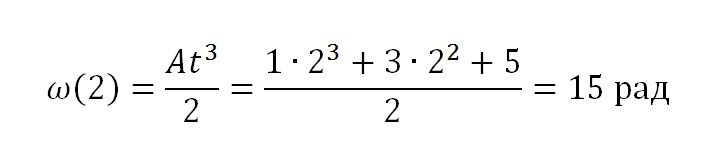
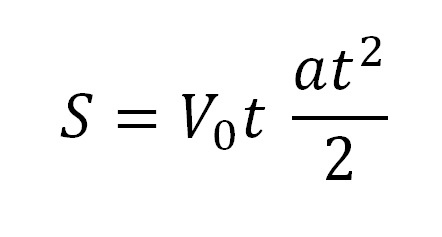
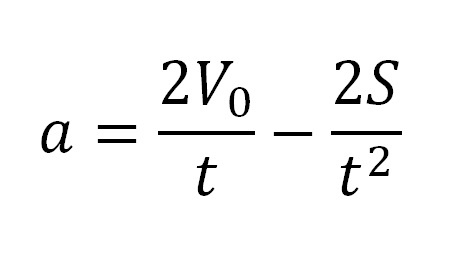
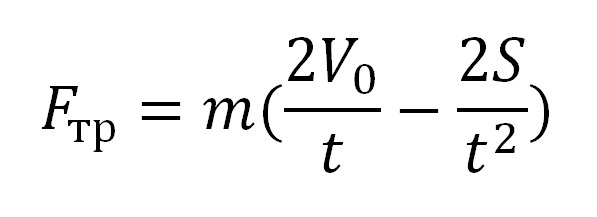
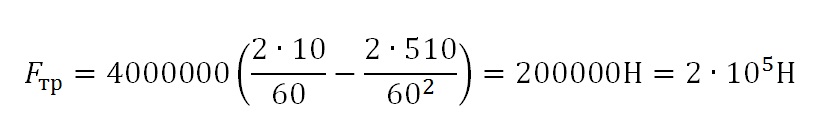
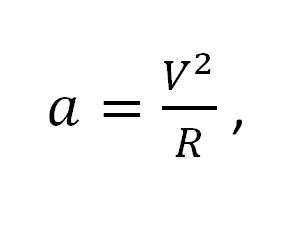
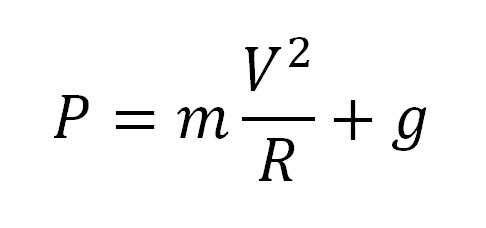
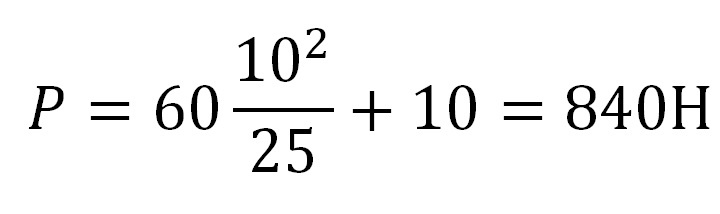
Бесплатно отвечаем на ваши вопросы. Задайте свой вопрос и получите ответ от профессионального преподавателя. Выберите лучший ответ.
Вопросы могут задавать только авторизованные пользователи. Войти