Гугл документы онлайн: что это такое, как работать
В современном мире обработка файлов играет важную роль как в работе, так и в обучении. Одним из самых популярных вспомогательных в этом деле сервисов является Google Документы. Приводим подробные инструкции, как с ним работать.
Что такое Google Документы
Гугл Документы (англ. «Google docs») — бесплатный онлайн-сервис для работы с различными видами документов: с текстовыми файлами, таблицами, презентациями и т.д. Все файлы пользователя при этом хранятся на сервере компании разработчиков Google.
Плюсы и минусы работы в Google Документах
Как и у любого другого сервиса, у Гугл Докс есть преимущества и недостатки. Рассмотрим их подробнее:
Плюсы:
- сервис абсолютно бесплатный для работы в личных целях;
- пользователь может зайти в свой аккаунт с любого устройства и продолжить с него работу;
- к одному и тому же файлу могут получить доступ несколько человек, что делает возможной командную работу;
- сервис имеет функцию автосохранения, поэтому данные не теряются;
- есть функция внутреннего поиска;
- есть возможность добавить больше функций с помощью официальных дополнений.
Минусы:
- при желании иметь повышенный уровень защиты и дополнительные возможности для командной работы придется приобрести подписку на бизнес-версию G Suite Essentials, стоимость которой — 10$/мес.;
- программа веб-ориентированная, это значит, что доступ к своим файлам пользователь может получить только при наличии интернет-соединения (если они не были скачаны на устройство);
- при потере доступа к аккаунту (например, блокировка) теряется доступ ко всем его документам;
- функциональность меньше, чем у аналогичных программ Microsoft Office, которыми все привыкли пользоваться.
Как войти
Чтобы начать пользоваться Google Docs, достаточно пройти регистрацию и сделать вход в аккаунт Google, зайти на официальный сайт в раздел Google Документы и выбрать нужный вам план: для личных целей (вы сможете сразу приступить к работе) или для бизнеса (для начала необходимо внести плату).
Как открыть документ
Если уже есть созданные вами файлы в аккаунте или те, к которым есть доступ, открыть их довольно просто: они все отображаются в окне выбора файлов:
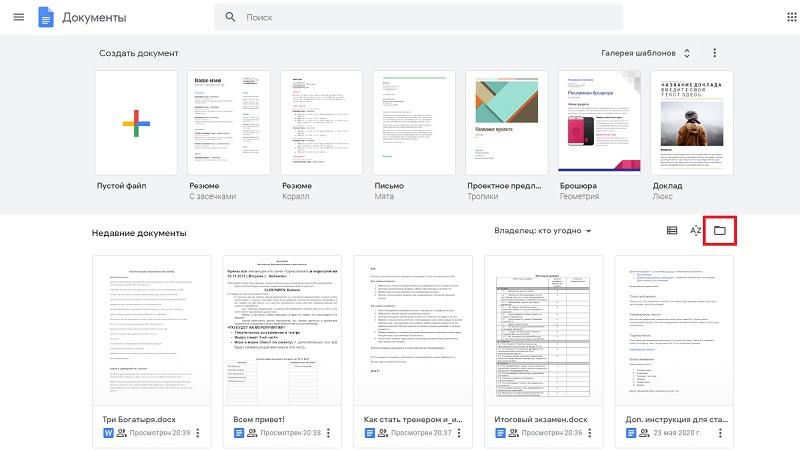
Также возможно найти последние файлы, с которыми вы работали недавно — в разделе недавних документов:
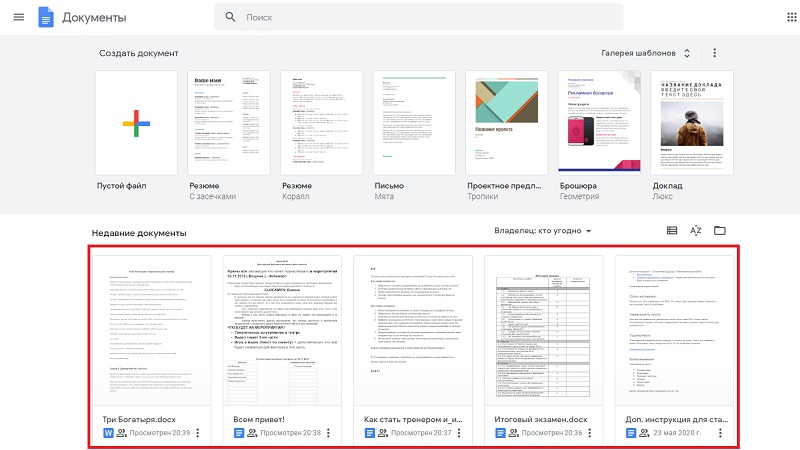
Кроме того, вы можете воспользоваться функцией поиска документов по названию:
Как создать документ
Есть два варианта создания файла: первый — использовать готовые шаблоны, сделанные под разные форматы. Найти их можно на главной странице:

Второй вариант — создать пустой файл, перейдя по ссылке или нажав на соответствующий раздел:

Выглядеть он будет так:

Как работать с текстом
Работа с текстом в Google Docs не требует особых усилий, достаточно лишь знать основы редактирования, а удобный интерфейс и возможность найти нужную информацию в разделе «Справка» облегчит задачу.
Панель инструментов
Панель расположена в верхней части экрана, а при наведении курсором на любую из иконок на ней отображается короткое описание функции. Помимо этого, почти у каждой из них есть свои горячие клавиши — сочетание клавиш, активирующие функцию.
Рассмотрим каждую функцию отдельно:
- Функция отмотки действия назад (Ctrl+Z) или вперед (Ctrl+Y):
![Функция отмотки действия Функция отмотки действия]()
- Печать (Ctrl+P):
![Печать Печать]()
- Проверка грамматики и орфографии (Ctr+Alt+X):
![Проверка грамматики и орфографии Проверка грамматики и орфографии]()
- Копирование форматирования:
![Копирование форматирования Копирование форматирования]()
- Изменение масштаба в процентах:
![Изменение масштаба в процентах Изменение масштаба в процентах]()
- Стили текста:
![Стили текста Стили текста]()
- Выбор шрифта:
![Выбор шрифта Выбор шрифта]()
- Размер шрифта:
![Размер шрифта Размер шрифта]()
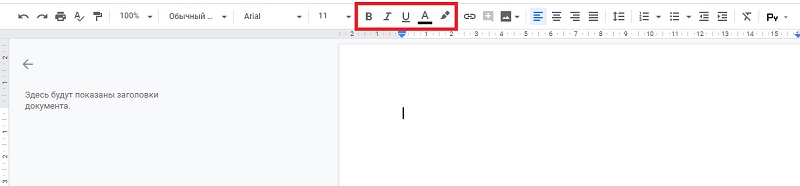
- Пять функций, позволяющие настроить вид текста: сделать его полужирным (Ctrl+B), курсивом (Ctrl+I), подчеркнутым (Ctrl+U), выбрать цвет текста и цвет фона текста:
![Пять функций Пять функций]()
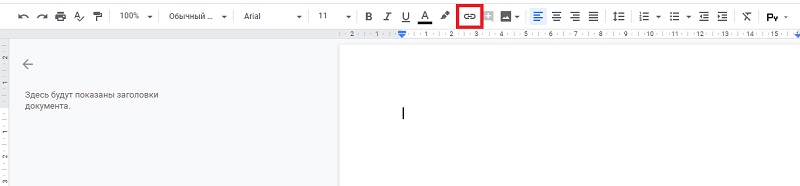
- Вставка ссылки (Ctrl+K):
![Вставка ссылки Вставка ссылки]()
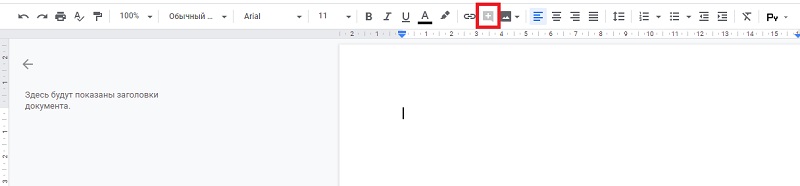
- Добавление комментария (Сtrl+Alt+M):
![Добавление комментария Добавление комментария]()
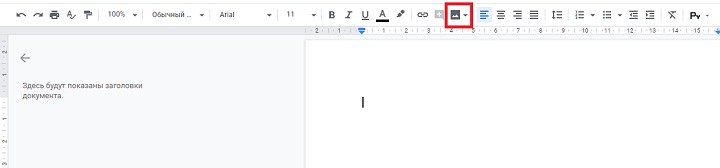
- Вставка изображения:
![Вставка изображения Вставка изображения]()
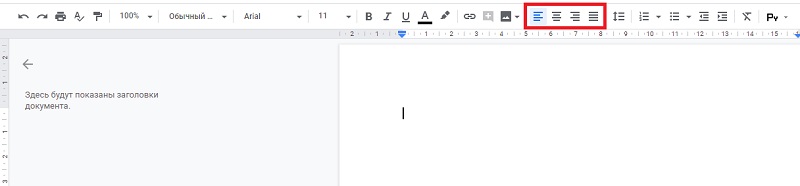
- Настройка выравнивания: по левому краю (Ctrl+Shift+L), по центру (Ctrl+Shift+E), по правому краю (Ctrl+Shift+R), по ширине (Ctrl+Shift+J):
![Настройка выравнивания Настройка выравнивания]()
- Настройка межстрочного интервала:
![Настройка межстрочного интервала Настройка межстрочного интервала]()
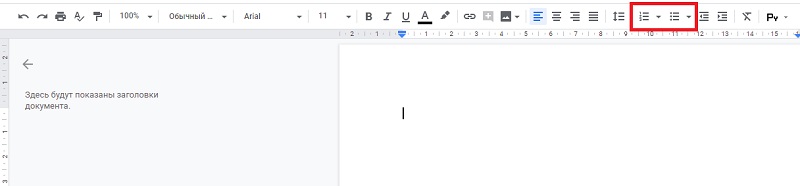
- Нумерованные (Ctrl+Shift+7) и маркированные (Ctrl+Shift+8) списки:
![Нумерованные и маркированные списки Нумерованные и маркированные списки]()
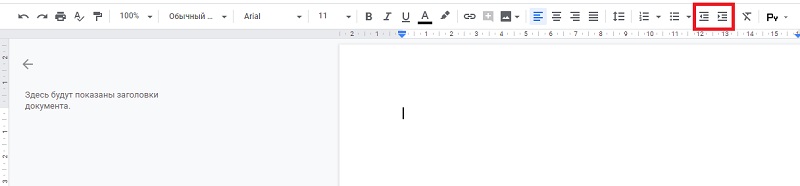
- Уменьшение (Ctrl+[) и увеличение (Ctrl+]) отступа:
![Уменьшение и увеличение отступа Уменьшение и увеличение отступа]()
- Очистка форматирования (Ctrl+\):
![Очистка форматирования Очистка форматирования]()
- Способы ввода (Ctrl+Shift+K):
![Способы ввода Способы ввода]()
Изображения
Раздел вставки используется для работы с изображениями, таблицами, рисунками и т.д.:
Изображение можно загрузить с устройства или виртуальных дисков, также можно вставить его ссылкой.
Списки
При работе со списками используется тот же принцип, что и во всех текстовых редакторах: активация с помощью соответствующих иконок; автоматическое продолжение списка при одиночном нажатии клавиши «Enter».
Таблицы
Их можно найти в том же разделе вставки:
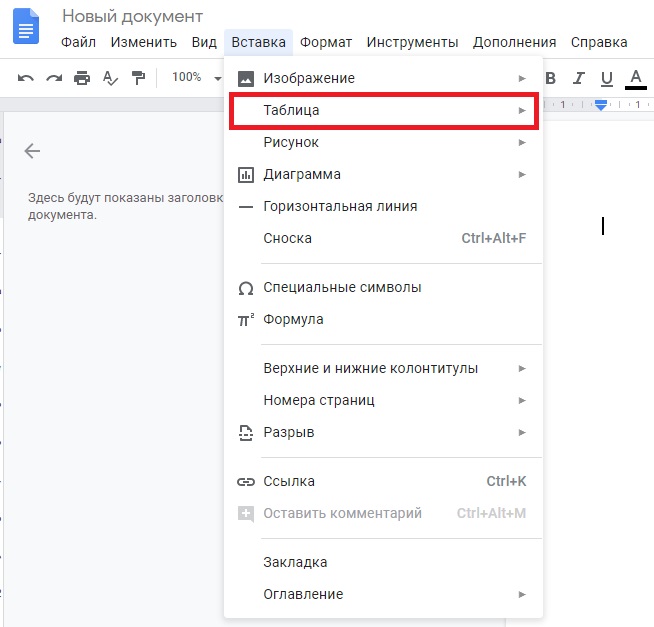
Пользователь вручную выбирает размер таблицы, максимальный — 20 столбцов на 20 строк.

Диаграммы
Находятся там же:
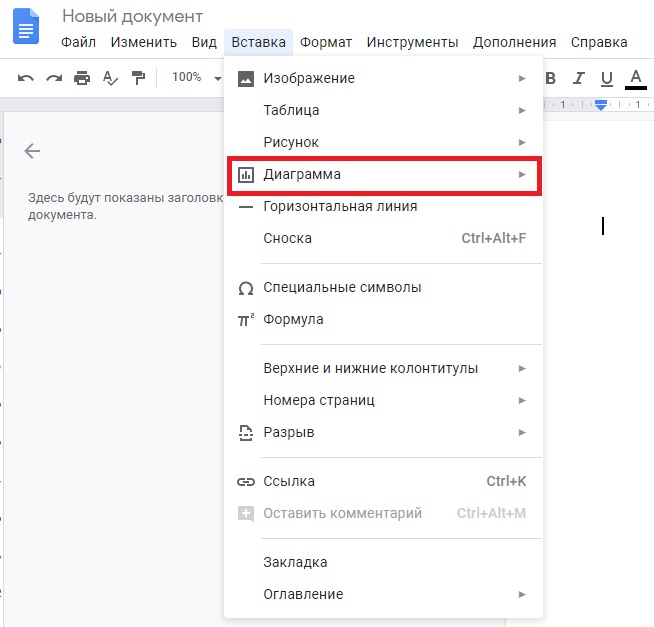
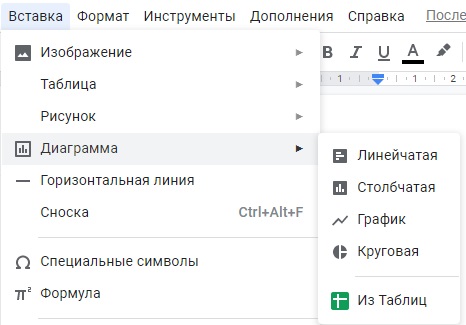
Допустимо четыре вида диаграмм, каждую из которых можно настроить, используя необходимые пользователю данные, а также есть возможность загрузить диаграмму из другого сервиса — Гугл Таблицы (Sheets):
Рисунки
Расположение — уже знакомая нам «вставка». Есть два варианта создания рисунка — создать новый или загрузить с диска.
Формулы
Функция позволяет использовать различные математические символы и конструкции:

Она задействует буквы греческого алфавита, математические символы, знаки отношений и стрелки.

Номер страницы
Этот раздел позволяет настроить номера страниц, их расположение и начальное значение.

Колонтитулы
Как и у многих других функций, у колонтитулов есть горячие клавиши как для верхних (Ctrl+Alt+О+H), так и для нижних (Ctrl+Alt+O+F).


Сноски
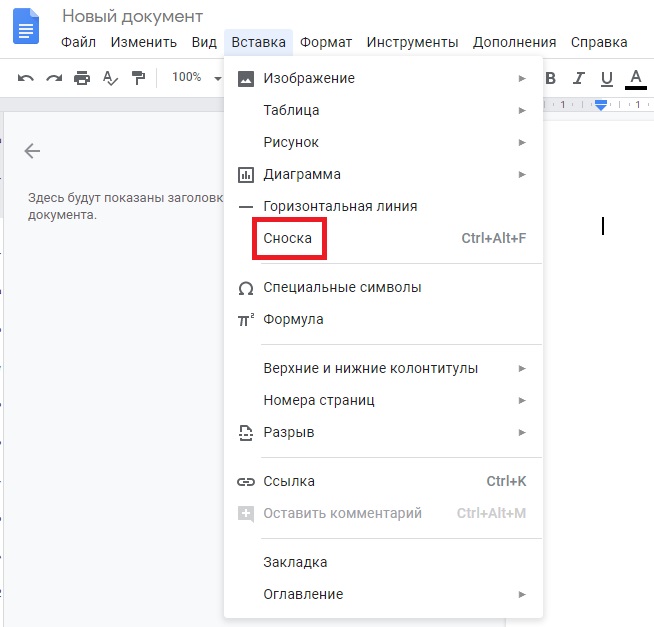
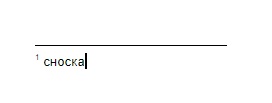
При клике на «Сноску» или при использовании горячих клавиш (Ctrl+Alt+F) автоматически оформляется подстрочная сноска:
Оглавление
Гугл Документы позволяют создавать иерархию с помощью стилей текста, это делит текст на главы и подглавы. Название каждой из них отображается слева от рабочего поля. Кроме того, они кликабельны, то есть при клике на них можно перемещаться по файлу.

Как вставить документ в Google Документ
Единственным вариантом вставки документа в Google Docs является гиперссылка, то есть вам нужно оформить в тексте активную ссылку на уже существующий внешний файл.
Как сделать Google Документ с общим доступом
В верхнем правом углу находится раздел «Настройки Доступа»:
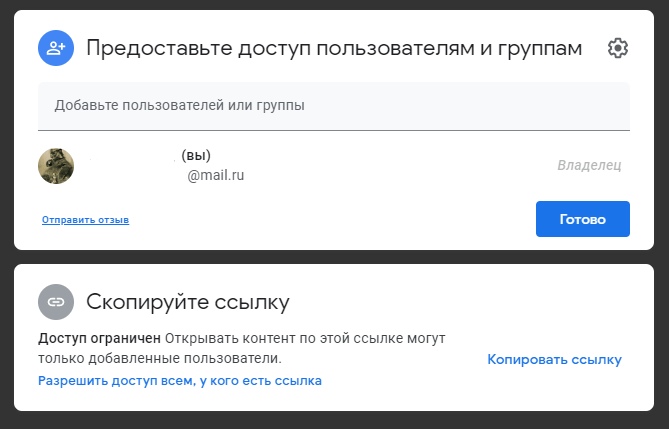
В нем можно определить, каким пользователям или группам можно просматривать или редактировать ваш файл, а также скопировать ссылку на него.
Как сохранить
В сервисе работает автосохранение, то есть, никаких дополнительных действий, чтобы сохранить текст, не требуется.
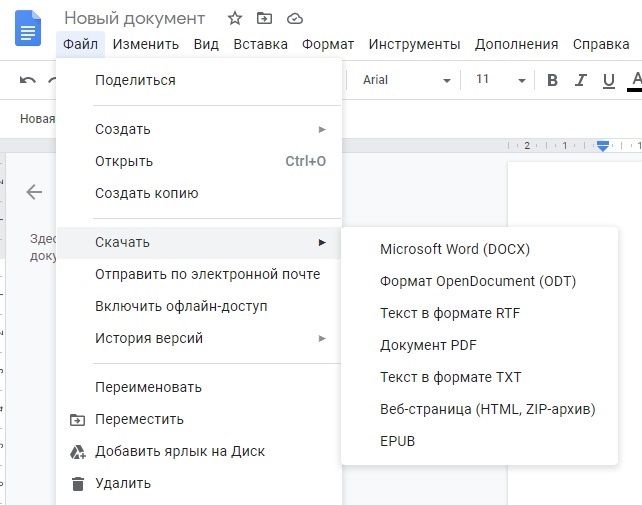
Как сохранить документ на компьютер
В разделе «Файл» в правом верхнем углу есть пункт «Скачать», где можно выбрать нужный формат и сохранить файл в любое место на устройстве.
Надеемся, что данная статья поможет вам в пользовании Гугл Документами. А в написании научных и учебных работ поддержат авторы Феникс.Хелп. Более 16 000 специалистов уже сейчас готовы связаться с вами!
Как правильно оформлять ссылки на интернет-источники
В этой статье мы расскажем об интернет-источниках и о том, как оформить на них ссылки по государственному стандарту.
Что такое интернет-источники
Интернет-источники (или интернет-ресурсы; веб-источники; веб-ресурсы) — это описание, являющееся частью библиографической записи и позволяющее получить представление о его содержании — по ГОСТу 7.82 от 2001 года. При заимствовании информации интернет-источника с дальнейшим ее использованием в научных, исследовательских работах, документах и т. д., ресурс нужно указывать по правилам ГОСТа.
Виды интернет-ресурсов
Наиболее точной является следующая классификация интернет-ресурсов:
- По доступности для пользователя:
- открытые — сервисы предоставляют информацию любому пользователю;
- полуоткрытые — для доступа к информации требуется создать личную учетную запись, то есть зарегистрироваться;
- закрытые — доступ к ресурсу предоставляется избранным пользователям.
- По расположению:
- общедоступные сайты;
- локальные сайты (размещенные в рамках локальной сети);
- сайты, доступ к которым можно получить доступ при наличии съемного носителя информации.
- По объему, виду предоставляемой информации и услуг:
- интернет-порталы — структура совмещенных функционально самостоятельных сайтов;
- информационные ресурсы — тематические сайты (узкоспециализированные) и порталы (широкоспециализированные, с возможностью пользователей общаться в пределах портала);
- интернет-представительства владельцев бизнеса — сайты, предоставляющие услуги и реализующие торговлю: сайт-визитка, где размещена актуальная информация (к примеру, контактная) о владельце сайта, интернет-магазин, где пользователь может заказать товар из каталога и прочее;
- веб-сервисы — сайты, предоставляющие возможность выполнения различных операций: почтовые сервисы для обмена информацией среди пользователей, поисковые сервисы для поиска нужной информации и прочее;
- комбинированные веб-сервисы — стандартные и специализированные социальные сети.

По какому ГОСТу оформлять
Актуальным является «ГОСТ Р 7.0.5-2008. Библиографическая ссылка. Общие требования и правила составления», все ссылки должны оформляться соответственно ему.
Как оформить сноску
Существует несколько способов создания ссылки на тот или иной веб-ресурс, и наиболее распространенным является сноска (подстрочная ссылка), об оформлении которой пойдет речь.
Порядок расположения
Допустимо три вида расположения библиографических ссылок, отличающиеся расположением относительно текста документа:
- Внутритекстовые ссылки. Размещают в самом тексте, чаще всего посредством пояснительной конструкции (скобок).
- Затекстовые ссылки. Создаются вынесением за текст, в выноску. Одним из вариантов затекстовых ссылок может являться список использованной в тексте документа литературы;
- Подстрочные ссылки. Создаются вынесением из текста под полосу документа, в сноску.

Основные правила
В соответствии с требованиями актуального ГОСТа выделяют перечень основных правил оформления сносок:
- нумерация сносок начинается на каждой странице и обозначается арабскими цифрами или астерисками (звездочками);
- фамилии и инициалы авторов цитируемых работ выделяются курсивом, инициалы следуют после фамилии, пробела между ними нет;
- названия цитируемых работ должны быть полными; они не заключаются в кавычки;
- данные о цитируемой работе оформляются в порядке, предусмотренном для оформления списка библиографии, в конце указывается URL (Uniform Resource Locator — Единый Указатель Ресурса) веб-ресурса, на который делается ссылка;
- оформление сносок в печатных изданиях и электронных документах различается: в первом случае приводятся выходные данные работ: количество томов, издательство, место и год издания, страница. Рассмотрим второй случай, при ссылке на веб-ресурс:
Нужно написать заглавие, указать общий характер материала ([Электронный ресурс]), сведения, которые относятся к заглавию, если таковые есть, данные об ответственности, об издании, объем ресурса, сведения о месте, имени и дате издания, обязательные примечания о виде интернет-ресурса по доступности для пользователя и об источнике основного заглавия, URL и дата обращения (чч.мм.гггг открытия автором текста, оформляющим ссылку, данного документа).
- при повторном цитировании одной и той же работы указываются только необходимые данные — отсылка к предшествующей сноске с указанием страницы или без, если она расположена на этой же странице; фамилия, инициалы автора, название, номер страницы, если сноска не предшествующая;
- при неточном цитировании нужно указать соответствующий текст в работе;
- после указания источника цитаты допускаются комментарии автора документа к сноске, отделяются длинным тире;
- форматирование сносок: шрифт — Times New Roman; размер —10 пунктов; выравнивание по ширине; отступ первой строки 5 мм; одинарный междустрочный интервал.
Примеры
При ссылке на печатное издание:
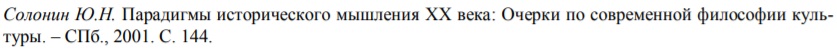
При ссылке на веб-ресурс:

Как нельзя оформлять ссылки на веб-ресурсы
Особенное внимание нужно обратить на следующее:
- Сведения об интернет-источнике необходимо указывать в полном объеме, потому что при их отсутствии в сноске ссылка может быть неточной и указывать на несколько документов с похожими сведениями.
- URL нужно сделать действительным и активным в документе, доступ к которому можно получить онлайн. Активным URL можно сделать с помощью гиперссылки — части гипертекстового документа, которая ссылается на другой элемент. Советуем делать это внимательно, так как при малейшем изменении исходного URL направление может произойти на другой ресурс либо оказаться недействительным.
Пользуясь советами нашей статьи, вы всегда сможете грамотно оформить ссылку на интернет-ресурс. А если вам понадобится помощь в учебе, вы всегда можете обратиться к авторам «Феникс.Хелп». Более 16000 специалистов уже готовы связаться с вами!
Оформление чертежей по ГОСТ и ЕСДК 2026
Оформление чертежей ЕСКД
Появление единой системы конструкторской документации в России обусловлено не только необходимостью систематизировать чертежи внутри страны, но и потребностью выставлять продукцию на мировой рынок. По всему миру установлены примерно одинаковые критерии оформления.
Соблюдать требования ГОСТа и ЕСКД нужно, потому что чертеж — графический документ, который имеет такую же силу, как и письменный. Без знания правил не получится ни успешно сдать экзамены в вузе, ни выполнить заказ работодателя.
При оформлении чертежа обратите внимание на следующие параметры:
- формат листа;
- рамка;
- масштаб;
- шрифт;
- линии.
Расскажем подробнее о каждом из этих пунктов.
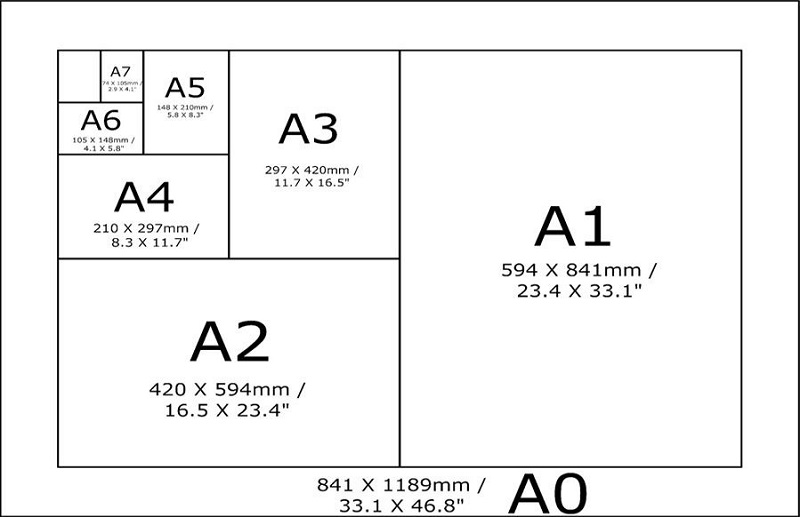
Форматы
В мире доминируют две системы классификации размера листа: международная и североамериканская. Правила ЕСКД требуют использования международных стандартов.
Студенческие чертежи чаще всего выполняют на листах формата А3 (297х240 мм), проектные работы — на А2 (420×594 мм), А1 (594×841 мм) и А0 (841×1189 мм), в зависимости от габаритов объекта. В частных случаях используют формат А4, например, если нужно изобразить небольшой фрагмент или деталь. Также на листах А4 оформляют спецификацию — документ, который систематизирует номенклатуру изделия.
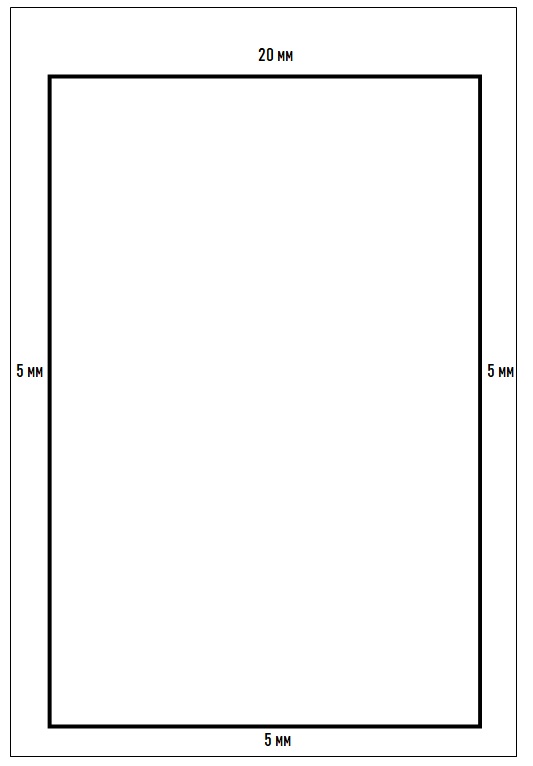
Рамка чертежа ГОСТ
Расположение рамки зависит от того, вертикально или горизонтально изображен объект. Если чертеж скомпанован вертикально, отступ от верхнего края листа должен быть равен 20 мм, а от всех остальных — 5 мм. При горизонтальном расположении расстояние 20 мм должно быть между рамкой и левым краем листа, остальные отступа также должны составлять 5 мм. Обводится рамка сплошной толстой линией.
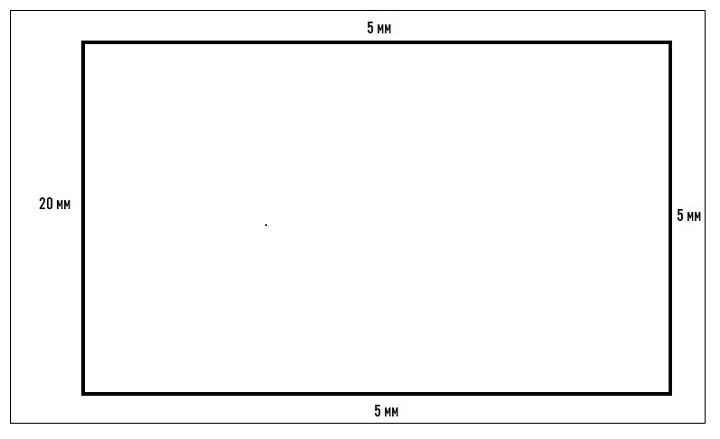
Заполнение штампа: пример
Штамп или, как принято его называть, основная надпись — это информация о чертеже, которая должна быть оформлена в нижнем правом углу листа в продолжение рамки. Слева располагаются дополнительные графы к основной информации.
Если чертеж выполнен на формате А4, то основная надпись занимает все основание листа:
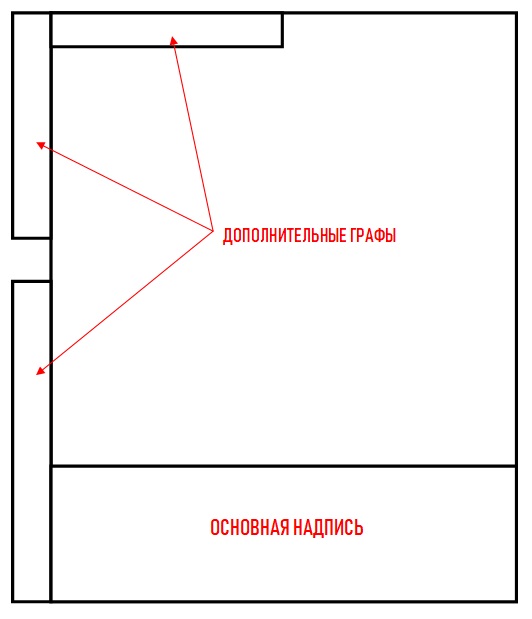
На форматах больше, чем А4, основная надпись смещается в нижний правый угол:
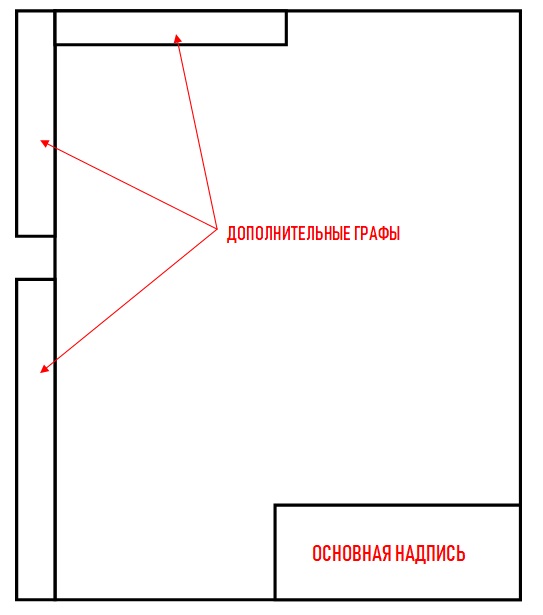
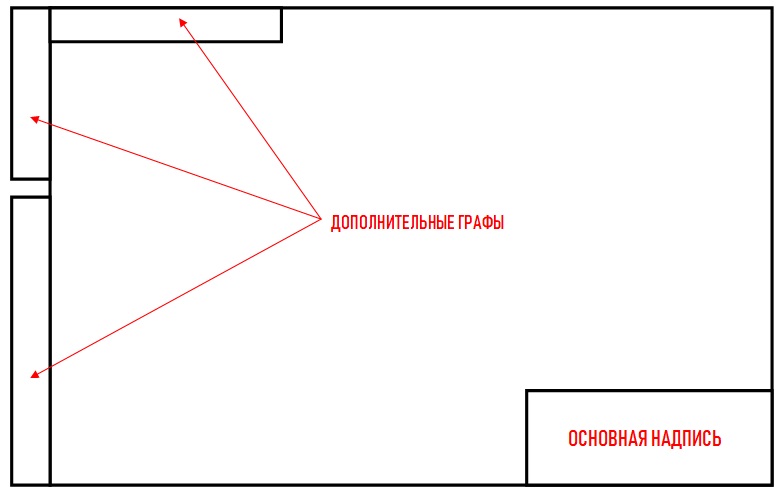
Обводятся эти графы сплошной толстой линией, а текст внутри — сплошной тонкой.
В ЕСКД прописано несколько форм основной надписи, в зависимости от предназначения чертежа. В архитектурных и инженерных вузах используют упрощенные версии. Рассмотрим пример заполнения одной из них.
Заполнение основной надписи: образец
Информация, которую нужно внести в основную надпись:
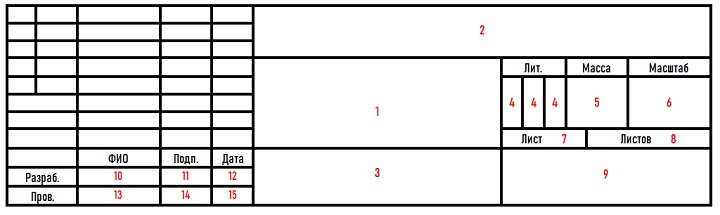
- Наименование изделия.
- Код документа (индекс раздела курса черчения, например ПЧ — проекционное черчение, ГЧ — геометрическое черчение и т. п.).
- Обозначение материала.
- Литера, присвоенная изображаемому предмету.
- Масса изделия в килограммах.
- Масштаб.
- Порядковый номер листа.
- Общее количество листов.
- Наименование исполнителя чертежа (например, сокращение названия учебного заведения и шифр группы).
- Фамилия исполнителя.
- Подпись исполнителя.
- Дата выполнения.
- Фамилия преподавателя.
- Подпись преподавателя.
- Дата проверки.
Образец заполненной основной надписи:
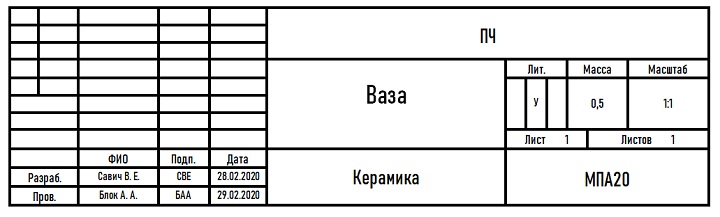
В незаполненных графах может быть указана информация о доработке и/или изменении чертежа.
Таблица на чертеже
Текстовая часть может быть оформлена в виде таблицы. В этот раздел обычно вносят техническое задание, размеры и другие параметры, которые невозможно отобразить графически или условными обозначениями. Такие таблицы располагают параллельно основной надписи ниже чертежа или справа от него.
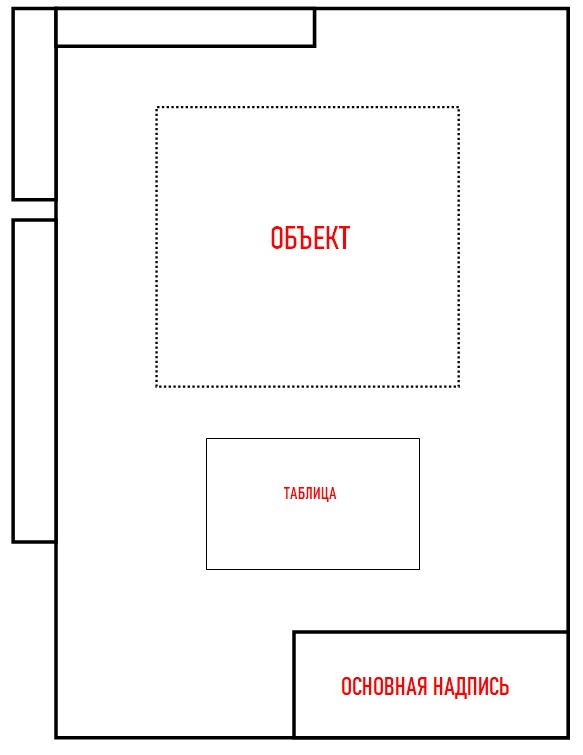
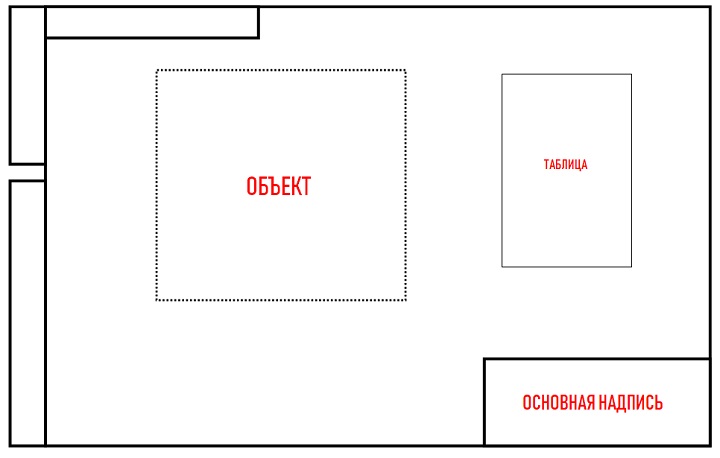
Таблица должна быть понятной. Название, если оно есть, нужно указать сверху.
Масштаб
Масштаб — соотношение величин, изображенных на чертеже, с действительными размерами изделия. Если формат позволяет выполнить чертеж в масштабе 1:1, то есть в натуральную величину, его следует изображать именно так.
Такое возможно достаточно редко, так что реальные размеры изделия уменьшают или увеличивают. Соотношение указывают в основной надписи как «масштаб уменьшения» или «масштаб увеличения».
Шрифты чертежные
В ГОСТе описаны шрифты, которые необходимо использовать при оформлении. В стандартах определены высота и ширина букв и цифр, толщина обводки, расстояние между буквами, словами и строками. Допускается 10 размеров шрифта (измеряется величиной заглавной буквы): 1,8; 2,5; 3,5; 5; 7; 10; 14; 20; 28; 40. Буквы и цифры могут находиться под углом в 75°, либо не иметь наклона вообще.
Высота шрифта обозначается буквой «h», то есть заглавные буквы равны 1h. Строчные буквы, как правило, равны 0,7h. Ширину принято обозначать буквой «d», где d=0,1h. Ширина большинства заглавных букв составляет 6d, а строчных — 5d, но есть исключения. Так, заглавные «А, Д, М, X, Ц, Ы, Ю» равны 7d, «Ж, Ф, Щ, Ш, Ъ» — 8d, «Г, 3, С» — 5d. Строчные «а, м, ц, ъ» — 6d, «ж, т, ф, ш, щ, ы, ю» — 7d, «з, с» — 4d.
Элементы букв, выходящие из формата шрифта («й», «ц» и т. п.), изображаются в пустом пространстве между строчками, то есть при расчете длины и ширины буквы не учитываются.
В ученических чертежах также используется узкий архитектурный шрифт с немного другими пропорциями:

При выполнении текстовой части чертежа учитывайте следующие правила:
- надписи выполняются от руки;
- высота всех знаков на чертежах должна быть не менее 3,5 мм;
- одинаковые элементы различных знаков следует выполнять одним и тем же приемом (помогает выработать автоматизм);
- необходимо строго соблюдать конструкцию каждой буквы и соотношение длины и ширины;
- расстояние между буквами должно быть зрительно одинаковым;
- все надписи должны быть выполнены аккуратно.
Линии чертежа
Для удобства прочтения чертежа разные по смыслу линии отличаются друг от друга видом и шириной обводки:
- Сплошной толстой линией (основной) выделяются видимые контуры изделия. Ширина обводки обозначается буквой «S» и находится в диапазоне от 0,4 до 1,4 мм.
- Сплошная тонкая — линия выносных и размерных линий, контур наложенного сечения, штриховка, выноски, полки выносок и подчеркивание надписей. Диапазон ширины — S/3.. S/2.
- Пунктир — изображение невидимых очертаний предмета, длина штриха может быть от 2 до 8 мм, а расстояние между ними — 1-2 мм. Ширина штриха — S/3..S/2.
- Штрихпунктир — обозначение осевых линий и линий центра окружностей. Длина штрихов — от 5 до 30 мм, расстояние между ними — 2-3 мм. Ширина штриха — S/3..S/2.
- Утолщенный штрихпунктир — элементы, расположенные перед секущей плоскостью, и поверхности, подлежащие термообработке или покрытию. Длина штриха — от 3 до 8 мм, расстояние между ними — от 3 до 4 мм, ширина — S/3..S/2.
- Разомкнутая линия — линия сечения. Длина штрихов — от 8 до 20 мм, ширина — 1,5S.
- Сплошная волнистая линия — обрывы, разграничение вида и разреза, ширина — S/3..S/2.
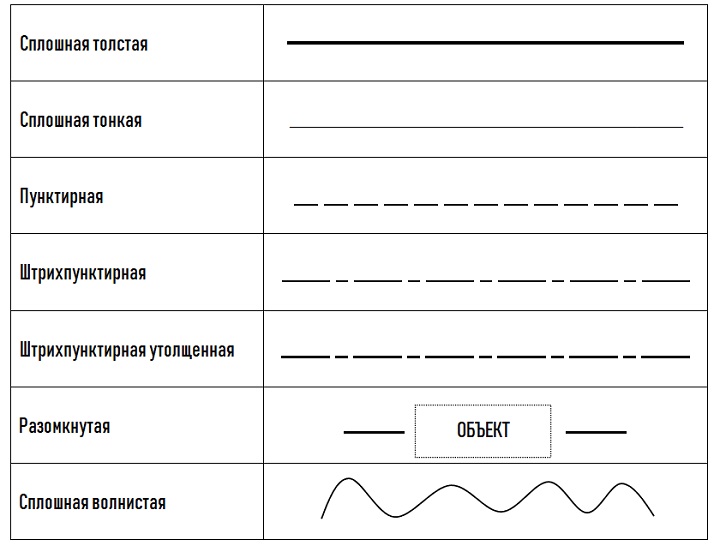
Длины штрихов и ширина обводки зависят от размера и сложности чертежа, причем сплошная тонкая линия всегда тоньше, чем пунктирная, штрихпунктирная или волнистая. Обычно в ученический набор изографов или рапидографов входят 3-4 инструмента с разными диаметрами. Например, 0,1, 0,2 и 0,4. Не стоит выполнять работу чертежными принадлежностями, близкими по диаметру (0,2, 0,35 и 0,4), такой чертеж будет плохо читаем.
Оформление чертежа — скрупулезный и требующий особой концентрации процесс. Вы можете снизить уровень стресса, постоянно практикуясь и время от времени обращаясь за помощью к специалистам Феникс.Хелп.
Социальная карта студента
Ответы на основные вопросы о выпуске, содержании, восстановлении и переоформлении социальной карты москвича.
Что такое социальная карта студента
Социальная карта москвича для студента — это банковская карта, которая дает разнообразные льготы.
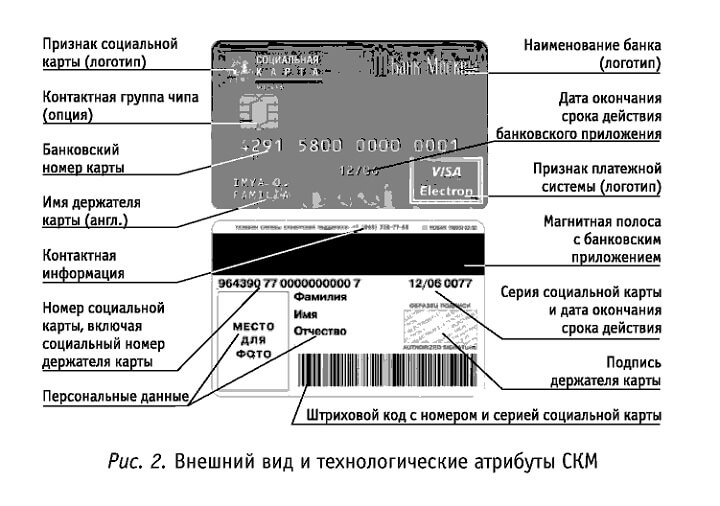
На пластиковой карте отображается личная информация студента:
- имя и фамилия;
- образовательное учреждение;
- фотография;
- номер полиса ОМС.
Кто может получить
Студенты, ординаторы и аспиранты дневной (очной) формы обучения, которые занесены в реестр.
Учебное заведение, в котором они числятся, должно либо находиться, либо быть зарегистрировано в Москве. Таким образом, учащиеся филиалов московских вузов тоже могут претендовать на получение льготной карты.
Какие есть льготы
- льготный проезд по Москве: один раз в месяц учащийся оплачивает безлимитный проезд в общественном транспорте (метро и наземный транспорт отдельно), сумма выходит гораздо меньше, чем при постоянной оплате даже картой «тройка»;
- льготный проезд на пригородные поезда: билеты на электричку стоят на 50% меньше;
- скидки: многие кафе, магазины, аптеки, театры, музеи и другие торгово-сервисные предприятия — в общей сложности более 7500 организаций — делают скидку до 20%;
- льготные условия банка: бесплатное годовое обслуживание.
Кроме того, социальной картой можно пользоваться как полноценной банковской, в том числе и при покупках в интернет-магазинах, и использовать ее в качестве полиса ОМС.

Сколько действует карта
Выдается обучающемуся на 5 лет, в случае перевыпуска — до конца срока обучения.
Как оформить
Для оформления соц. карты в 2026 году необходимы:
- заявление (образец есть на официальном сайте);
- документ, удостоверяющий личность;
- сведения о регистрации и фактическом месте проживания;
- СНИЛС;
- фотография размером 3х4.
Через Госуслуги
Подать заявление на выпуск можно онлайн, в личном кабинете портала «Госуслуги». Все указанные документы необходимо предоставить в отсканированном виде, а фотографию обязательно в формате JPEG. Забирают готовую карту в отделении МФЦ или, в некоторых случаях, в учебном заведении.
МФЦ
Также карту можно оформить, придя лично в центр госуслуг «Мои документы» и предоставив оригиналы документов из списка и напечатанную фотографию.
Сколько изготавливается
Официальные сроки изготовления — до 30 дней. Но обычно, если никаких дополнительных вопросов от МФЦ не поступает, изготовление длится 2-3 недели. Статус готовности можно посмотреть на «Госуслугах» или узнать по телефону.
Получает карту либо держатель лично по паспорту, либо официальный представитель с документами, подтверждающими его полномочия.
Блокировка карты
Причины
- карта повреждена, утеряна или украдена;
- истек срок действия;
- аннулирована вузом;
- воспользовался не ее владелец.
Как разблокировать
Восстановить карту возможно как онлайн на Официальном Сайте Мэра Москвы, так и в офисе МФЦ.
Не работает социальная карта студента в метро
Перестает работать в следующих случаях:
- нужно пополнить баланс;
- повредилась или размагнитилась;
- заблокирована.
В таком случае сначала необходимо убедиться, что баланс в порядке, а затем обратиться за восстановлением к сотруднику кассы метро.
Если карту изъяли и заблокировали из-за нарушения правил пользования, вернуть ее можно в сервисном центре «Московский транспорт».
Перевыпуск карты при утере
Если карта утеряна или украдена, необходимо сразу же заблокировать ее и банковский счет, ко которому она привязана. Это делается по телефону в службе поддержки и в банке. Затем надо написать заявление на перевыпуск онлайн или в МФЦ.
Специально блокировать и перевыпускать карту в случае смены паспорта не требуется.
Если на утерянной карте были неиспользованные средства, то предоставляется временный билет. Что нужно сделать, чтобы его получить? Учащийся должен обратиться в сервисный центр «Московский транспорт» и предоставить следующее:
- документ, удостоверяющий личность;
- студенческий билет или справка об обучении из вуза;
- номер заявления на перевыпуск (будет выдан, как только вы оформите заявление);
- квитанцию об оплате, если она есть.
1. улица 1905 года, дом 25.
2. улица Старая Басманная, дом 20, корпус 1.
Телефон: +7 (495) 539-54-54 или 3210 (с мобильного).
Как пополнить
Пополнение возможно непосредственно в кассах метро и наземного транспорта или в билетопечатающих автоматах.
Где смотреть серию и номер
Серия и номер карты отображаются на обратной стороне, а банковский номер — на лицевой.
Помните, что вы всегда можете обратиться за помощью в учебе к специалистам Феникс.Хелп. Более 16000 авторов уже готовы с вами связаться!
Музыкальные вузы России и Москвы
На сегодняшний день любой желающий может попасть в музыкальный вуз: академию, консерваторию, университет или училище. Рассказываем о лучших высших учебных заведениях Москвы и всей России, обучении в них и порядке поступления.
Как поступить в музыкальный вуз
Экзамены
Как и в любом другом вузе РФ, для поступления необходимо сдать соответствующие ЕГЭ. Обычно требуется обязательная сдача экзаменов по двум предметам: русский язык и литература, но некоторые направления требуют сдачи и других дисциплин, например, истории.
Помимо ЕГЭ, обязательно нужно пройти дополнительные вступительные испытания (ДВИ).
Дополнительные вступительные испытания
Одно из них зависит от факультета, второе одинаково для всех направлений — экзамен по сольфеджио (дисциплина, изучающая нотную грамоту и развивающая слух), который обычно включает в себя:
- написание музыкального диктанта;
- пение по нотам с тактированием незнакомой мелодии;
- пение любой гаммы;
- пение главных трезвучий, их обращения; септаккордов; доминантсептаккордов, их обращения;
- определение на слух аккордов.
Третий экзамен по музыкальной грамоте, включает в себя различные для каждого из направлений части, к примеру, для фортепианного и струнного отделения:
- чтение хроматических гамм мажора и минора;
- построение от звука аккордов;
- демонстрирование знания пауз, длительностей, ступеней гаммы, основных видов метра и видов тональностей, названий элементов грамоты (октав и пр.), знаков в ключе мажорной и минорной тональности, знаков альтерации (диез, бемоль, бекар), обозначений мажорных и минорных тональностей, квинтового круга тональностей;
- демонстрирование умения играть на фортепиано гаммы (мажорные и минорные), ноты в басовом и скрипичном ключах, увеличенные и уменьшенные интервалы (с последующим разрешением).
Четвертый экзамен проводится в форме коллоквиума — определения преподавателем глубины знаний музыкальной литературы и истории музыки в форме разговора.
Кроме того, необходимо исполнить произведение (романс, этюд, сонату и пр.) на самостоятельно выбранном инструменте, уровень сложности зависит от требований конкретной организации (при поступлении на дирижирование или музыкальную теорию произведение исполняется на фортепиано).
Документы
Перечень необходимых документов:
- заявление с просьбой о поступлении;
- паспорт или другой документ, удостоверяющий личность;
- аттестат, диплом или любой другой документ, удостоверяющий предыдущее образование;
- информация о результатах ЕГЭ (достаточно просто указать действительные баллы);
- медицинскую справку формы 086/y;
- две фотографии 3х4;
- военный билет (если имеется).
Если абитуриенту на момент поступления еще не исполнилось 18 лет, он обязан прийти с родителем или официальным представителем. Некоторые вузы позволяют принести согласие на обработку персональных данных, подписанное родителем/представителем, но эту информацию нужно уточнять на официальном сайте учебной организации.
Помимо этого, некоторые учебные заведения в обязательном порядке требуют свидетельство об окончании ДМШ (Детской музыкальной школы), в особенности отделения фортепиано, скрипки, аккордеона-баяна. Другим же вузам и отделениям, например, эстрадного или классического вокала, его предоставлять желательно, если есть.
Порядок действий
Чтобы успешно поступить в высшее учебное заведение, а еще лучше — на бюджетной (то есть бесплатной) основе, нужно придерживаться следующего порядка действий:
- Определиться с вузом и отделением заранее.
- Узнать, какие ЕГЭ требует желаемое место поступления.
- Сдать ЕГЭ на необходимое количество баллов.
- Подать копии документов в вуз в числах, указываемых на официальном сайте.
- Пройти дополнительные вступительные испытания.
- Дождаться публикации рейтинга поступающих и отслеживать его.
- В случае поступления подать заявление о согласии на зачисление и подлинники аттестата и/или диплома.
Лучшие музыкальные вузы Москвы

Топ-4 вузов Москвы:
- Московская государственная консерватория имени П.И. Чайковского — 11 программ.
- Государственный музыкально-педагогический институт имени М.М. Ипполитова-Иванова — 11 программ.
- Академия хорового искусства имени В.С. Попова — 2 программы.
- Российская академия музыки имени Гнесиных — 39 программ.
Лучшие музыкальные вузы России
На данный момент страна предоставляет возможность обучения в более ста музыкальных высших учебных заведениях по всей России, как узкой, так и широкой специализации. Представляем вам список лучших образовательных учреждений с разными направлениями.
Звукорежиссура
Краснодарский государственный институт культуры
Музыкальная журналистика
Казанская государственная консерватории им. Н.Г. Жиганова
Московская государственная консерватория имени П. И. Чайковского
Музыкальный продюсер
Данную специальность может получить человек, окончивший факультет «менеджмент музыкального искусства», «медиакоммуникации» и пр.
Санкт-Петербургский государственный институт культуры
Учитель музыки
Чтобы работать учителем музыки, нужно закончить факультет музыкального образования или дошкольного образования и музыки — зависит от того, где именно вы хотите работать.
Московский информационно-технологический университет МАСИ
Театрально-музыкальные вузы
Российский институт театрального искусства
Российская академия музыки имени Гнесиных
Музыкальная критика
Работать по специальности музыкальной критики можно, окончив программу музыковедения, культурных исследований, музыкознания, музыкально-прикладного искусства и т.п.
Волгоградский Государственный Институт Искусств и Культуры
Военно-музыкальные вузы
Единственное в Вооруженных силах РФ учебное заведение музыкального направления:
Московское Военно-музыкальное Училище
Заочное обучение в музыкальном вузе

Далеко не в каждый современный музыкальный вуз можно поступить на заочную форму обучения, потому что получение профессионального образования требует больших усилий и постоянной практики, однако современные технологии все-таки позволяют обучаться на заочном отделении или дистанционно. Одним из обязательных условий поступления на заочку является наличие среднего специального музыкального образования — техникум или колледж.
Чаще всего на музыкальную заочку поступают будущие преподаватели музыки и музыкальные руководители, так как теории в таком обучении больше, чем практики.
Заочное обучение могут предложить такие вузы, как Институт Современного Искусства, Российский университет театрального искусства.
Кстати, за помощью в обучении вы всегда можете обратиться к авторам Феникс.Хелп. Более 16000 тысяч специалистов уже готовы связаться с вами.