Предел функции: примеры решений

Рассмотрим понятие и определение предела, разберем основные решения пределов.

Разбор записи предела на математическом языке

Любой предел состоит из трех частей:

1. Знак «lim», который, собственно, и определяет существование предела.
2. Записи под знаком «lim», которая может приобретать вид \(x\rightarrow a,\) \(x\rightarrow0\) и \(x\rightarrow\infty\). Такая запись читается «икс стремится к а (может принимать любое число)/нулю/бесконечности». На практике, переменная «х» может быть записана и другой буквой.
3. Функции f(x) под знаком предела.

Для наилучшего понимания рассмотрим конкретный пример \(\lim_{x\rightarrow1}\frac{3x^2-2x-5}{x+3}\).

Данная запись читается так: «предел функции \(\lim_{x\rightarrow1}\frac{3x^2-2x-5}{x+3}\) при икс стремящемся к единице». Что же значит выражение «икс стремится к единице»?

Понятие предела, в отличие от большинства известных математических понятий, динамическое, то есть нет какого-то статичного, неменяющегося числа или тождества в качестве его определения. Построим последовательность: 

Разберем следующий важный вопрос – а что значит выражение «икс стремится к единице»? И что вообще такое «стремится»? Понятие предела – это понятие, если так можно сказать, динамическое. Построим последовательность:

x=1,1, x=1,01, x=1,001, ... x=1,00000001, ...

Все данные значения x и разница между ними настолько малы и близки к одной точке (в данном случае к единице), что можно сказать, что «икс» последовательно принимает значения, которые бесконечно близко приближаются к единице и практически с ней совпадают. Это и означает «икс стремится к единице».

Предел последовательности: определение и свойства

Предел последовательности, как и предел функции, является одним из основных понятий математического анализа. По сути, каждое вещественное число может быть представлено в виде последовательности максимально приближенных к нему чисел.

Вещественные (действительные) числа обозначаются как ε (эпсилон) и принадлежат множеству R, которое включает в себя все натуральные, целые, рациональные и иррациональные числа.

Теперь обратимся к определению предела последовательности и разберем, что же оно означает.

То есть, основываясь на знании определения последовательности (пронумерованный и строгий набор каких-либо объектов, в математике — числе, которые можно записать в виде \(x_{1,}\;x_{2,\;}\;x_{3,}\;x_4\;...\;x_n\) ), мы утверждаем, что существует какая-то окрестность, все точки которой имеют такое значение, что при вычитании предела a из x_n , модуль результата будет меньше заданного ε.

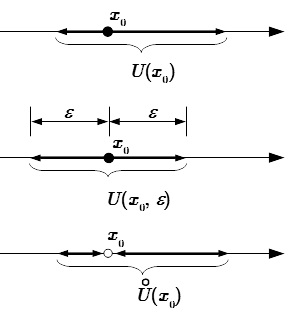
Для лучшего восприятия понятия «окрестность» рассмотрим следующее изображение:

Окрестностью в данном случае являются интервалы слева и справа от x₀, причем окрестность может быть проколотой (третий случай), то есть сама точка x₀ не входит в заданный интервал.

На математическом языке данное определение записывается следующим образом:

\(\lim_{x_0\rightarrow a}\;x_n=a\) или \(x_n\rightarrow a\)

Это выражение равносильно двойному неравенству a - ε < x_n < a + ε, которое означает, что точки x _n, начиная с некоторого номера n>N, лежат внутри интервала (a-ε , a+ε), т.е. попадают в какую угодно малую ε-окрестность точки а.

Свойства

1. Постоянный множитель c можно выносить за знак предела. На математическом языке данное утверждение выглядит так:

\(\lim_{n\rightarrow\infty}\;(c\times x_n)=cA=c\;\lim_{n\rightarrow\infty}\;x_n\) В данном случае n стремится к бесконечности, то есть мы имеем неопределенно большое количество значений x₀ . Теперь докажем это свойство. Примем \(\lim_{n\rightarrow\infty}\;x_n\) за A, тогда переменную \(x_n\) мы можем представить в виде:

\(x_n=A+a_n\)

где \(a_n\) — бесконечно малая величина. Очевидно, что:

\(c\times x_n=c(A+a_n)=cA+ca_n\). Так как \(ca_n\) является бесконечно малой величиной, то \(сA\) — предел последовательности \(\left\{c\times x_n\right\}\). Свойство доказано.

2. Если существуют конечные пределы последовательностей \(x_n\) и \(y_n\), то

\(\underset{}{\lim(x_n\pm y_n)=\lim_{}(}x_n)\;\pm\underset{}{\lim(y_n)}\)

\(\underset{}{\lim(x_n\times y_n)=\lim_{}(}x_n)\;\times\underset{}{\lim(y_n)}\)

\(\underset{}{\lim\frac{x_n}{y_n}=}\;\frac{\lim_{}(x_n)}{\underset{}{\lim(}y_n)}\) (только если \(\underset{}{\lim(}y_n)\) не равно нулю)

Докажем теперь и это свойство. Пусть \(\underset{}{\lim(}x_n)=A\) и \(\underset{}{\lim(}y_n)=B\). В таком случае \(x_n\) и \(y_n\) мы можем представить в виде:

\(x_n=A+\alpha_n\)

\(y_n=B+\beta_n\)

где \(\alpha_n\) и \(\beta_n\) — некоторые бесконечно малые величины.

Тогда \(x_n\pm y_n=(A\pm B)+(\alpha_n\pm\beta_n)\)

Учитывая, что \((\alpha_n\pm\beta_n)\) — бесконечно малая величина, получаем:

\(\lim_{}(x_n\pm y_n)=(A\pm B)=\lim_{}(x_n)\pm\lim_{}(y_n) \) Аналогично:

\(x_n\times y_n=(A\pm\alpha_n)(B\pm\beta_n)=AB+(B\alpha_n+A\beta_n+\alpha_n\beta_n)\)

Осталось распознать в выражении \( (B\alpha_n+A\beta_n+\alpha_n\beta_n)\) бесконечно малую величину, что влечет за собой:

\(\lim_{}(x_n\times y_n)=AB=\lim_{}x_n\times\lim_{}y_n\\\\ \)

Далее покажем, что отношение \(\frac{x_n}{y_n}\) можно представить в виде:

\(\frac{x_n}{y_n}=\frac AB+б/м\)

Очевидно, что:

\(\frac{x_n}{y_n}=\frac{A+\alpha_n}{B+\beta_n}=\frac AB+(\frac{A+\alpha_n}{B+\beta_n}-\frac AB)=\frac AB+\frac{B\alpha_n-A\beta_n}{B(B+\beta_n)}\) где \(\frac{B\alpha_n-A\beta_n}{B(B+\beta_n)}\rightarrow\frac0{B^2}=0\) при \(n\rightarrow\infty\)

Следовательно:

\(\underset{}{\lim\frac{x_n}{y_n}}=\frac AB=\underset{}{\frac{\lim_{}x_n}{\lim_{}y_n}\;\lim}\\\\x_n\times\lim_{}y_n\)

Что и требовалось доказать.

3. Если существуют конечные пределы последовательностей \(\left\{y_n\right\} и \left\{y_n^p\right\}\), то \(\underset{}{\lim\;}y_n^p={(\underset{}{\lim\;}y_n)}^p\).

Определенного доказательства данного свойства нет, однако интуитивно мы можем провести следующие умозаключения.

Пусть \(\underset{}{\lim\;}y_n=A,\) тогда:

\(y_n=A+\alpha_n\)

где \( \alpha_n\) – некоторая бесконечно малая величина.

Следовательно:

\(y_n^p={(A+\alpha_n)}^p=A^p{(1+\frac{\alpha_n}A)}^p\rightarrow A^p{(1+0)}^p=A^p=\underset{}{(\lim}y_n)^p\)

Что и требовалось доказать.

Предел функции

Обратимся сразу к определению.

Постоянное число А называется пределом функции f(x) при x→a, если, задав некоторое произвольное, как угодно малое положительное число ε, можно найти такое δ >0 (зависящее от ε), что для всех x, лежащих в ε-окрестности числа а, т.е. для x, удовлетворяющих неравенству 0 < x-a < ε , значения функции f(x) будут лежать в ε-окрестности числа А, т.е. |f(x)-A| < ε.

Данное определение называют «определением по Коши». В предыдущих пунктах было рассмотрено «определение по Гейне», которое, по сути, тоже является определением предела функций, но на языке последовательностей. Зачем же нужны два различных по формулировке, но идентичных по смыслу определения? Это необходимо для того, чтобы в будущем, при решении задач или доказательстве каких-либо утверждений, опираться на более удобную для обоснования формулировку, ведь компоненты в них все-таки отличаются друг от друга.

Непрерывность функции

Функция y=f(x) называется непрерывной в точке х = а, если существует предел функции в этой точке.

Записать данное определение на математическом языке можно следующим образом:

\(\lim_{x\rightarrow a}f(x)=f(a)\)

Для того, чтобы функция являлась непрерывной, обязательно должны выполнятся 3 условия:

1. Функция y = f(x) определена в точке х=а (существует f(a)).
2. Существует предел \(\lim_{x\rightarrow a}\;f(x)\) функции в точке х=а.
3. Предел функции в точке х=а равен значению функции в этой точке \((\lim_{x\rightarrow a}f(x)=f(a))\).

Существуют и другие определения, которые, как и в случае с определением пределов по Коши и по Гейне, различаются по формулировке для наиболее удобного использования.

Функция y = f(x) непрерывна в точке х=а, если для любого числа ε>0 существует такое число δ>0, что для всех х, удовлетворяющих условию \(\vert x–a\vert<\delta\), выполняется неравенство \(\vert f(x)–f(a)\vert<\varepsilon\).

Если функция y=f(x) непрерывна в каждой точке некоторого промежутка, то её называют непрерывной на данном промежутке.

Также можно дать определение непрерывности справа или слева от точки.

То есть, \(f(x_0+0)\equiv\lim_{x\rightarrow x_0+0}f(x)=f(x_0)\) или \(f(x_0-0)\equiv\lim_{x\rightarrow x_0-0}f(x)=f(x_0)\).

Вычисление пределов

Рассмотрим примеры вычисления пределов.

Простейшие пределы

Для начала обратимся к простейшему пределу, который был рассмотрен в самом начале: \(\lim_{x\rightarrow1}\frac{3x^2-2x-5}{x+3}\)

В данном случае можно попробовать просто подставить единицу (так как предел стремится к единице) в выражение. Тогда:

\(\lim_{x\rightarrow1}\frac{3x^2-2x-5}{x+3}=-1\)

Да, это работает только с простейшими пределами, которые, на самом деле, на практике встречаются не редко, так что попробовать просто подставить икс в выражение — одно из возможных решений.

Теперь попробуем сделать то же самое с пределом, который стремится к бесконечности.

Икс стремится к бесконечности \((x\rightarrow\infty)\) означает, что икс неограниченно возрастает (например, х=10, х=100, х=1000, х=10000 и так далее).

Рассмотрим предел \(\lim_{x\rightarrow\infty}(1-x)\) и подставим в функцию (1-x) бесконечность. Получается, что функция стремится к минус бесконечности. В данном случае метод «подстановки» тоже работает.

Итак, когда мы видим простейший предел, сначала нужно попробовать подставить в функцию «х».

Выражения для самостоятельного решения:

\(\lim_{x\rightarrow3}\frac{x^2+7}2 ; \lim_{x\rightarrow\infty}(x^4+8x+10) ; \lim_{x\rightarrow0}\frac1{x^2}\)

Пределы с неопределенностью вида \(\frac\infty\infty\)

Неопределенность вида \(\frac\infty\infty\) появляется, когда мы пытаемся подставить «х» в предел стремящийся к бесконечности и имеющий дробную функцию:

\(\lim_{x\rightarrow\infty}\frac{2x^2-3x-5}{1+x+3x^2}\)

Кажется, что \(\frac\infty\infty=\infty\), однако это не так. Чтобы получить верный ответ, нужно провести некоторые вычисления. Их и рассмотрим далее.

Для начала находим и в числителе, и в знаменателе старшую степень икса, а затем выбираем наибольшую из них. В данном случае старшие степени числителя и знаменателя равны, однако это частный случай.

Теперь мы должны и числитель, и знаменатель разделить на х в старшей степени:

\(\lim_{x\rightarrow\infty}\frac{2x^2-3x-5}{1+x+3x^2}=\{\frac\infty\infty\}=\lim_{x\rightarrow\infty}\frac{{\displaystyle\frac{2x^2}{x^2}}-{\displaystyle\frac{3x}{x^2}}-{\displaystyle\frac5{x^2}}}{{\displaystyle\frac1{x^2}}+{\displaystyle\frac x{x^2}}+{\displaystyle\frac{3x^2}{x^2}}}=\lim_{x\rightarrow\infty}\frac{\displaystyle2-\frac3{x^{}}-\frac5{x^2}}{\displaystyle\frac1{x^2}+\frac1{x^{}}+3}\)

Затем анализируем дроби с иксом, мысленно подставляя вместо х бесконечность. Получается, что все эти дроби стремятся к нулю, соответственно, их можно принять за ноль. Значит:

\(\lim_{x\rightarrow\infty}\frac{\displaystyle2-\frac3{x^{}}-\frac5{x^2}}{\displaystyle\frac1{x^2}+\frac1{x^{}}+3}=\frac23\)

Рассмотрим еще 2 примера, чтобы в этом убедиться.

1. \(\lim_{x\rightarrow\infty}\frac{\displaystyle7x^3+15x^2+9x+1}{\displaystyle5x^4+6x^2-3x-4}\)

Поделив числитель и знаменатель на \(x^4\) и подставив бесконечность в получившиеся дроби (для закрепления материала лучше высчитать это самостоятельно), получаем:

\(\lim_{x\rightarrow\infty}\frac{0+0+0+0}{5+0-0-0}=\frac05=0\)

2. Проведем аналогичные вычисления над \(\lim_{x\rightarrow\infty}\frac{\displaystyle2x^2-3x-5}{\displaystyle x+1}.\) В итоге мы получаем \(\frac20\), однако нужно понимать, что делим мы не на ноль, а на бесконечно малое число, соответственно, ответом будет бесконечность.

Пределы с неопределенностью вида \(\frac00\)

Сразу же возникает логичный вопрос: почему мы делим на ноль, если каждый школьник знает, что на ноль делить нельзя? Если обратиться к определению предела, все встанет на свои места: дело в том, что мы работаем не с самим нулем, а с бесконечно малыми числами и функциями, однако для удобства записываем «0».

Решение пределов данного вида похоже на ранее рассмотренное решение пределов с неопределенностью вида \(\frac\infty\infty\). Различие лишь в том, что икс теперь стремится к конкретному конечному числу. 

Рассмотрим конкретные примеры и научимся решать подобные пределы.

1) \(\lim_{x\rightarrow-1}\frac{5x^2-2x-7}{x+1}\)

Как мы уже знаем, сначала нужно попробовать подставить -1 в выражение:

\(\lim_{x\rightarrow-1}\frac{5x^2-2x-7}{x+1}=\lim_{x\rightarrow-1}\frac{5{(-1)}^2-2(-1)-7}{(-1)+1}=\frac00\)

Отсюда мы и получаем неопределенность вида \(\frac00\).

Теперь запомним правило:

Почти всегда для этого необходимо решить квадратное уравнение и/или использовать ФСУ (формулы сокращенного умножения).

В знаменателе мы имеем x+1, это уже простейшая функция, так что знаменатель мы не трогаем.

Применяя стандартные операции для решения квадратного уравнения, раскладываем числитель и получаем (x+1)(5x-7).

Итак, \(\lim_{x\rightarrow-1}\frac{(x+1)(5x-7)}{x+1}.\)

Очевидно, что (х+1) в числителе и знаменателе можно сократить.

Получаем:

\(\lim_{x\rightarrow-1}5x-7=5(-1)-7=-12\)

Очень важно при разложении на множители замечать формулы сокращенного умножения! Они могут быть видны не сразу, а после проведения одного или нескольких шагов, например, вынесения числа за скобку.

2) Теперь рассмотрим предел все с той же неопределенностью вида \(\frac00\), но в функции которого появляются коренные выражения.

\(\lim_{x\rightarrow3}\frac{\sqrt{x+6}-\sqrt{10x-21}}{5x-15}\)

И снова, не придумывая ничего нового, сначала подставляем 3 в выражение, чтобы, собственно, и получить ту самую неопределенность \(\frac00\).

\(\lim_{x\rightarrow3}\frac{\sqrt{x+6}-\sqrt{10x-21}}{5x-15}=\frac{\sqrt9-\sqrt9}{15-15}=\frac00\)

Теперь, для того, чтобы упростить выражение, нужно избавиться от корней. Вообще, в математике стараются избавляться от иррациональности в любом случае, когда это возможно, — так гораздо проще жить.

А избавимся от иррациональности мы с помощью метода умножения числителя и знаменателя на сопряженное выражение. Этот метод работает не только при разности корней, но и при вычитании какого-либо числа из корня.

Что же это за метод? А основан он на всей известной формуле разности квадратов:

\(a^2–b^2\;=(a\;–\;b)(a\;+\;b)\)

В числителе уже есть один из множителей \(\sqrt{x+6}-\sqrt{10x-21}\), соответственно, сопряженный множитель, на который мы умножаем и числитель, и знаменатель, это \(\sqrt{x+6}+\sqrt{10x-21}\).

Получаем:

\(\lim_{x\rightarrow3}\frac{\sqrt{x+6}-\sqrt{10x-21}}{5x-15}=\lim_{x\rightarrow3}\frac{(\sqrt{x+6}-\sqrt{10x-21})(\sqrt{x+6}+\sqrt{10x-21})}{(5x-15)(\sqrt{x+6}+\sqrt{10x-21})} \)

Теперь, учитывая формулу в числителе дроби, проводим ряд преобразований и получаем:

\(\lim_{x\rightarrow3}\frac{(\sqrt{x+6}-\sqrt{10x-21})(\sqrt{x+6}+\sqrt{10x-21})}{(5x-15)(\sqrt{x+6}+\sqrt{10x-21})}=\lim_{x\rightarrow3}\frac{27-9x}{(5x-15)(\sqrt{x+6}+\sqrt{10x-21})}\)

Да, избавившись от иррациональности в числителе, мы обрели ее в знаменателе, однако оперировать суммой корней, которую мы получили, гораздо легче. И, вообще, можно сразу подставить в корни тройку и вынести полученное число за знак предела, как упоминалось об это ранее.

\(\lim_{x\rightarrow3}\frac{27-9x}{(5x-15)(\sqrt{x+6}+\sqrt{10x-21})}=\frac16\lim_{x\rightarrow3}\frac{27-9x}{5x-15} \)

А теперь просто раскладываем дробь на множители и получаем конечный ответ:

\(\frac16\lim_{x\rightarrow3}\frac{27-9x}{5x-15}=\frac16\lim_{x\rightarrow3}\frac{9(3-x)}{5(x-3)}=\frac16\lim_{x\rightarrow3}\frac{-9(x-3)}{5(x-3)}=\frac16\underset{x\rightarrow3}{\lim-}\frac95=-\frac3{10}\)

Примеры для самостоятельного решения:

\(\lim_{x\rightarrow3}\frac{x^2+x-2}{\sqrt{x+6}-2}, \lim_{x\rightarrow3}\;\;\frac{\;\sqrt{7-x}-2}{4-\sqrt{13+x}}\)

Мы рассмотрели основное понятие пределов функции и последовательности и разобрали классические варианты решения пределов.

Если же быстро разобраться в этой сложной теме не получается, а сдача важной работы не за горами, вы всегда можете обратиться к авторам ФениксХелп, которые помогут с решением.