Производная функции – одно из фундаментальных понятий в математике, без понимания которого становится невозможным решение большинства математических и физических задач. Что же это такое?

Производная функции — краткое описание, суть

Если совсем просто, то:

Выражаясь математическим языком, это предел отношения приращения функции к приращению её аргумента при стремлении приращения аргумента к нулю. Формула:

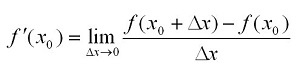
Она понимается в двух смыслах: геометрическом и физическом.

Геометрический смысл: производная от функции в точке равна тангенсу угла между осью OX и касательной к графику функции в данной точке.

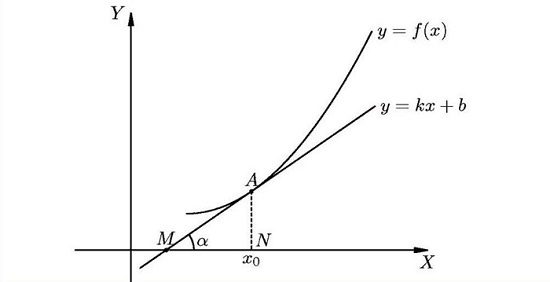
Физический смысл: производная пути по времени равна скорости прямолинейного движения. Таким образом, значение скорости в определённый момент времени t₀ определяется по формуле:

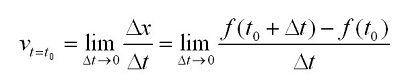
Вычисление производной называется дифференцированием. Обратный процесс – интегрированием.

Основные правила нахождения производных

Дифференцирование строится на следующих правилах.

Правило №1: производная от произведения числа на функцию равна

(c * f (x))' = c * f' (x),

где с – любое число.

Правило №2: производная от суммы функций равна

(f (x) + g (x))' = f ' (x) + g' (x).

Правило №3: производная от разности функций равна

(f (x) – g (x))' = f ' (x) – g' (x).

Правило №4: производная от произведения двух функций равна

(f (x) g (x))' = f ' (x) g (x) + f (x) g' (x).

Правило №5: производная от дроби равна

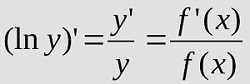
Существует и так называемая сложная функция (композиция функции) вида f (g(x)). В данном случае f (x) считается внешней функцией, g (x) – внутренней.

Правило дифференцирования сложной функции

Производная сложной функции вычисляется по формуле:

[ f (g (x))]' = f ' (g (x)) g' (x).

Пример нахождения

Задача: продифференцировать (x+2)¹⁰. Обозначим её как u=x+2.

Решение: так как (x¹⁰)'=10x⁹,

то ((x+2) ¹⁰)'=(u¹⁰)'=10u⁹⋅u'=10(x+2) ⁹⋅1=10(x+2) ⁹.

Ответ: 10(x+2) ⁹.

Логарифмическая производная

Вычисляется по формуле:

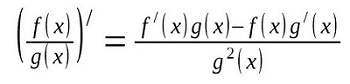
Часто применяется для упрощения дифференцирования некоторых функций.

Пример поиска производной

Пусть y = y(x).

Для удобства прологарифмируем данную функцию:

ln y = ln y(x).

Теперь вычислим производную по правилу дифференцирования сложной функции:

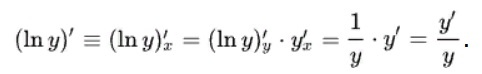
Из этого следует, что

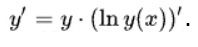
Тогда ответ:

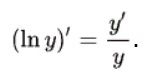
Производная обратной функции

Общая формула:

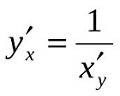
Формулы и пример решения

Производные обратных тригонометрических функций:

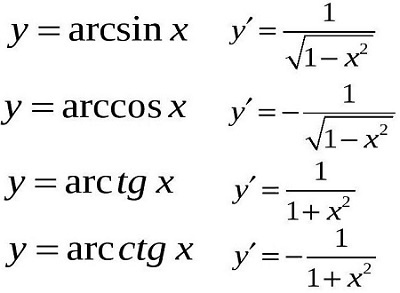
Задача: продифференцировать y=x²-7lnx.

Решение: находим по формуле

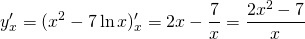
отсюда

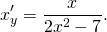
Производная функции, заданной параметрически

Пусть функция задана параметрическим уравнением:

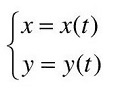
Тогда производная равна:

Формулировка, решение примеров

Задача: продифференцировать функцию.

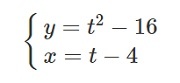
Решение: (при записи производной всегда необходимо писать t в нижнем индексе)

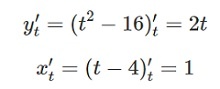
Подставляем в формулу:

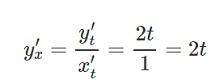
Ответ:

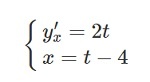
В ответе составляется система, в которой кроме полученной производной необходимо писать х = t – 4.

Производная неявной функции

Если функция у = у(х) задана уравнением F (x; y(x)) = 0 то говорят, что она задана неявно.

Теоретическое обоснование

Для нахождения производной неявной функции нужно:

1. Продифференцировать обе части уравнения по независимой переменной х предполагая, что у – это дифференцируемая по х функция.
2. Решить полученное уравнение относительно производной у' (х).

Решение в примерах

Задача: решить функцию , заданную неявно:

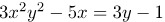
Решение:

1) перенесём 3у -1 в левую часть и дифференцируем обе части равенства

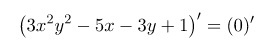
Получим

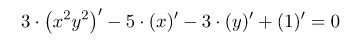
Считая, что у – это функция от х, находим производную как от сложной функции:

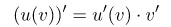
Тогда

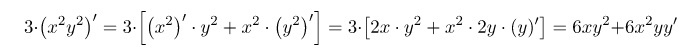
Для заданной функции имеем:

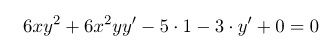
2) Решаем полученное уравнение относительно у':

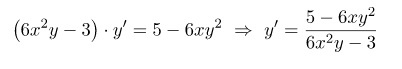
Ответ:

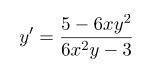
Полная таблица производных

Приводим табличную форму, которая существенно облегчает вычисления:

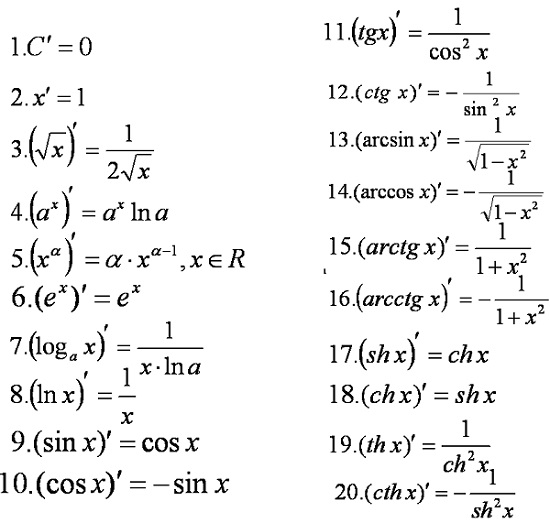
Формул из этого списка достаточно для дифференцирования любой элементарной функции.

Решение элементарных производных, примеры

Задача№1: найти производную функции

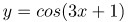
Решение: данная функция является сложной, поэтому

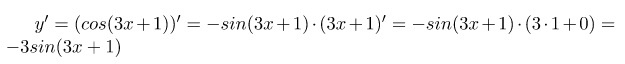
Ответ:

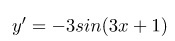
Задача №2: найти производную функции 

Решение:

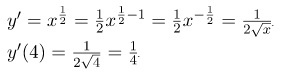
Ответ:

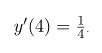
Изучение производных и интегралов занимает большое количество времени. ФениксХэлп может помочь вам в решении контрольных и самостоятельных работ по этой теме и многим другим.

Матрица — это прямоугольная таблица чисел, состоящая из определенного количества строк и столбцов. Существует множество матричных видов, и один из них — диагональный. Разберемся, что он из себя представляет.

Что такое диагональная матрица

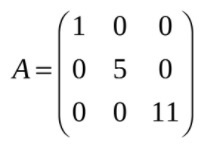
Напомним, что матрица считается квадратной, если количество строк равно количеству столбцов (m = n).

Особенности и свойства

Для начала нужно понять, что такое матричный определитель.

Определитель (детерминант) — это некоторая величина, с которой можно сопоставить любую квадратную матрицу.

Определитель А = (2×2), к примеру, вычисляется по формуле:

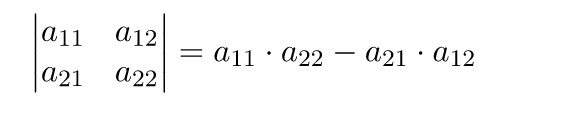
Из этого следует свойство №1: определитель диагональной матрицы равен произведению ее диагональных элементов.

Свойство №2: обратная матрица для диагональной равна:

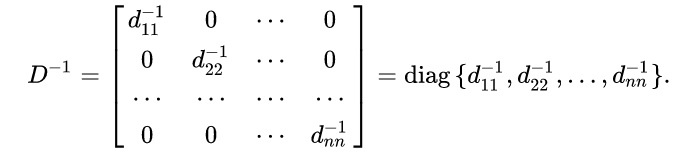
Свойство №3: ранг равен количеству ненулевых диагональных элементов.

Главная и побочная диагонали

Главную диагональ образуют элементы, расположенные на местах \(а_{11}\), \(а_{22}\), \(а_{33}\)…\(а_{NN}\). Их соответственно называют диагональными.  

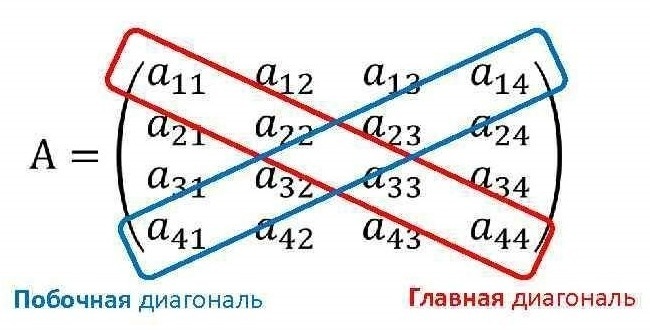
Побочной диагональю называют диагональ элементов от правого верхнего угла до нижнего левого. Эти диагонали параллельны друг другу.

Частные случаи диагональных матриц

Существуют три основных подвида: единичная, нулевая, скалярная.

Единичная матрица

У единичной матрицы все диагональные элементы равны единице.

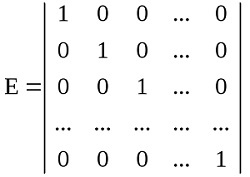
В формулах ее обозначают буквой Е.

Нулевая матрица

В нулевой матрице все элементы, в том числе диагональные, равны нулю.

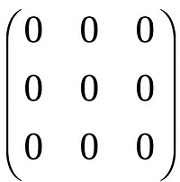
В формулах ее обозначают цифрой 0.

Скалярная матрица

В скалярной матрице все элементы на главной диагонали равны друг другу.

В некоторых случаях говорят, что скалярная матрица — это произведение скаляра на единичную матрицу Е. В ней диагональные элементы могут быть как положительными, так и отрицательными.

Примеры решения диагональных матриц

Иногда недиагональная матрица может быть приведена к диагональному виду.

Условие: дана матрица А

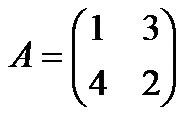
Задача: привести к диагональному виду.

Решение: характеристическое уравнение равно

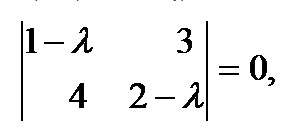
а его корни: \(λ_1 = 5\), \(λ_2 = (-2)\)

Если \(λ_1 = 5\), то

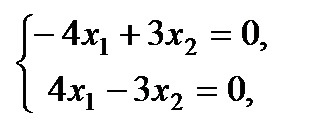
Пусть \(х_2 = с\), тогда вектор равен:

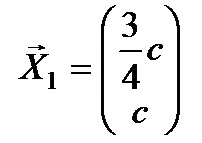
Если \(x = λ_2 = (-2)\), то

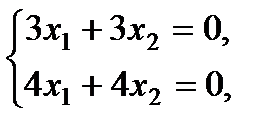
Пусть \(х_2 = с\), тогда вектор равен:

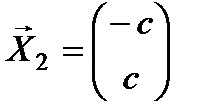
Таким образом, диагональная матрица имеет вид:

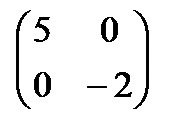
Изучение данных математических объектов имеет свои подводные камни. Если у вас нет времени на учебу, Феникс.Хелп может помочь вам с решением контрольных, самостоятельных и иных проверочных работ.

На данный момент самой известной системой компьютерной алгебры является MathCAD. Ее востребованность в технической и научной сферах объясняется рядом неоспоримых преимуществ перед аналогами. Что она из себя представляет?

Прикладная система MathCAD: что это, для чего нужна

Прикладная система MathCAD — это программа для инженерных математических расчетов и автоматизированного проектирования.

В «Маткад» входят инструменты вычисления, графики и программирования. Ее главными особенностями являются легкое интегрирование с системами САПР и возможность коллективной работы над проектами.

Общая характеристика, возможности

Программа имеет широкий спектр применения и предлагает следующие возможности:

• автоматическое преобразование единиц измерения;
• анализ результатов с помощью различных графиков;
• документирование с использованием расширенных математических обозначений;
• возможность представления расчетов с помощью различных инструментов графики в едином документе.

Также «Маткад» предоставляет научные и технические справочники, редакторы и видеоуроки. Бесплатный период составляет 30 дней, после истечения данного срока пользователь получает доступ к приложению PTC MathCAD Express — облегченную версию основной программы.

Главные отличия MathCAD от других расчетных программ

В отличие от большинства других программ, MathCAD не ограничивается инженерными расчетами и объединяет множество функций в одном ПО:

• решение математических уравнений и инженерных задач любой сложности;
• программирование;
• создание 3D-графики, гистограмм и диаграмм;
• создание комплексной документации;
• работа с компонентом Excel.

Также «Маткад» отличается от аналогов графическим режимом ввода выражений, что значительно упрощает работу с формулами и математическими обозначениями.

Помимо этого, софт переведен на русский язык и имеет удобный интерфейс для комфортной работы с большими проектами.

Возможности интеграции с другими программами

Открытое приложение поддерживает среду .NET и XML, что позволяет интегрировать систему MathCAD практически в любые IT-структуры. Также возможно интегрирование документа в модель Creo для двухмерного и трехмерного проектирования.

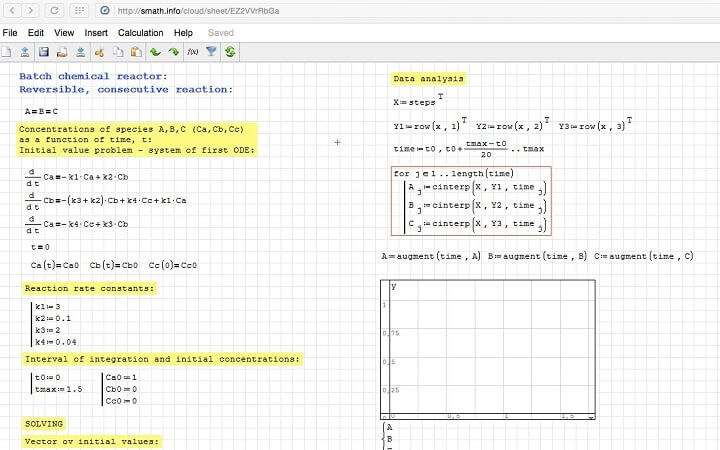
Бесплатные аналоги MathCAD

Бесплатные аналоги «Маткад» разнятся по своему назначению. Основными принято считать SMath Studio Cloud, Mas.Exponenta.ru и Graph Online. В сравнении с «Маткадом» они имеют ограниченный функционал и не предназначены для создания трехмерных графиков.

Можно ли работать в онлайн-режиме

В «Маткаде» нельзя работать в онлайн-режиме, однако программа предъявляет минимальные системные требования к установке на компьютер.

Понравилась статья? Феникс.Хелп может помочь в написании любых научных текстов, даже дипломов и диссертаций!

Мы уже знаем, что матрица – это объект, который представляет собой совокупность взаимосвязанных строк (m) и столбцов (n). С ней можно проводить различные действия, от обычного вычитания до транспортирования. Разберёмся с самой простой матричной операцией – сложением.

Сложение матриц — теория

Формула:

\(с_{ij} = a_{ij} + b_{ij}\)

где i – номер строки, а j – номер столбца.

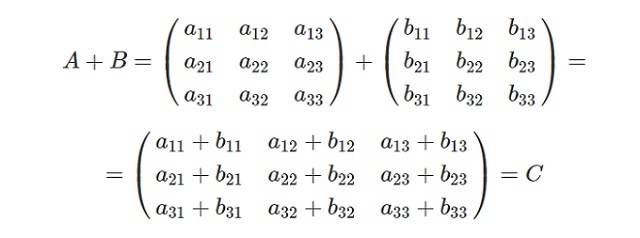
То есть, чтобы получить, например, элемент \(с_{11}\), нужно сложить \(а_{11}\) и \(b_{11}\). 

Когда это возможно, можно ли складывать матрицы разной размерности

Как сложение, так и вычитание матриц возможно только в том случае, когда они равны по размеру.

Также подметим, что нельзя складывать матрицы с обычными целыми числами и дробями. Порядок элементов в таблице менять нельзя.

Экономический смысл сложения матриц

Матрица имеет прикладное значение, так как часто используется в экономике для систематизации информации и облегчения вычислений. К примеру, с помощью неё можно предоставить отчёт о продажах:

Пусть \(х_{ij}\) – это количество определённого товара, проданного в определённом магазине за первый год. Матрица У – отчёт о продажах за второй год. Тогда, чтобы посчитать сумму продаж за оба года, нужно сложить отчёты Х и У.

Свойства операции сложения матриц

Свойств немного, и все они легки для запоминания:

1. Свойство коммутативности: A+ B = B + A.
2. Свойство ассоциативности: (A+ B) + C= A + (B + C).
3. Свойство дистрибутивности: (A+ B) * C= AC + BC.

При сложении А с нулевой матрицей 0, у которой все элементы равны нулю, исходная матрица не меняется:

А + О = А

При сложении А с противоположной матрицей (-А) сумма равна нулю:

А + (-А) = О

Примеры с решением на нахождение суммы матриц

Задача №1

Даны слагаемые:

Найти: С

Решение

\(с_{11} = а_{11} + б_{11} = 2 + 1 = 3\)

\(с_{12} = а_{12} + б_{12} = 3 + (-3) = 0\)

\(с_{21} = а_{21} + б_{21} = (-1) + 2 = 1\)

\(с_{22} = а_{22} + б_{22} = 4 + 5 = 9\)

Ответ:  

Задача №2

Даны слагаемые:

Найти: С

Решение: так как матрицы разного размера (А = 2 × 3; В = 3 × 2), данная операция невозможна.

Ответ: нет решения.

Не справляетесь с заданиями по учебе? Обращайтесь в ФениксХелп за помощью!

Сегодня принцип Парето считается одним из фундаментальных правил эффективности, которое можно использовать для оптимизации результатов любой деятельности. Как он был создан?

Вильфредо Парето — кто это, краткая история

Сам Вильфредо Парето, знаменитый экономист и социолог девятнадцатого века, никакого принципа не предлагал. Он изучал зависимости и законы распределения доходов в Италии и однажды пришёл к выводу, что 20% итальянских домохозяйств владеет 80% богатства.

На это исследование обратил внимание именитый учёный Джозеф Джуран. Именно он взял за основу данное соотношение 20/80 и предложил универсальное эмпирическое правило, которое может применяться во многих областях жизни.

Что такое принцип Парето простыми словами

Правило звучит так: 20% усилий дают 80% результата, а остальные 80% усилий — лишь 20% результата.

Из этого выводят несколько тезисов:

• только единичные действия приводят к важным результатам;
• большая часть усилий бесполезна;
• желаемый результат часто отличается от действительного.

Иными словами, минимальный набор основных действий принесёт больше результата, чем набор множества второстепенных.

На каком базовом соотношении основан

Соотношение 20/80 действительно встречается очень часто и уже принято как базовое. Однако критики данного принципа отмечают, что оно не всегда равно именно 20% на 80%, поскольку в реальной жизни на нашу деятельность влияет множество разных факторов.

Это означает, что формула Парето не должна рассматриваться как непреложный закон, который задан точными числовыми параметрами. Но она должна приниматься во внимание при организации работы и принятии решения о распределении средств.

Как применять правило 80 на 20

Есть подвох: даже зная, что только двадцать процентов действий принесут нужный результат, мы так или иначе вынуждены затрачивать остальные восемьдесят, поскольку работа просто будет не выполнена. Приведём пример: если в мясном магазине будут представлены только самые популярные и окупаемые виды, то количество продаж снизится, ведь потребителю всегда нужен выбор.

В таком случае, чем же полезно это правило? Оно учит нас тратить значительную часть усилий только на то, что принесёт пользу, но при этом не забывать о мелочах. Объясним на примерах.

Примеры из жизни и бизнеса

Правило может помочь избавиться от хлама в квартире. Ежедневно мы пользуемся лишь малой частью вещей, которыми владеем. При уборке работает такой метод: если что-то не использовалось более двух лет, то с этим можно распрощаться.

Закон Парето работает и в саморазвитии. Выбирая для глубоко изучения сферу, которая даётся вам легко, вы получите больше результата, чем при изучении сложной сферы.

Также он может помочь при составлении ежедневного расписания. В зависимости от своего биоритма человек чувствует себя бодрым в разное время суток. Соответственно, используя соотношение 20/80, нужно переносить большую часть важных дел на тот час, в котором вы чувствуйте себя энергичным, а неважное оставлять на потом.

Эффективная работа включает 80% труда и 20% отдыха. По этому же правилу устроены уроки и перемены в школе.

Теперь о бизнесе. В управлении и предпринимательстве действуют следующие закономерности:

• большая часть ресурсов тратится на содержание неэффективных процессов и сотрудников. Поэтому для модернизации производства необходимо сохранить 80% эффективности, избавившись от 20% ненужных ресурсов;
• большую часть прибыли получают от малой части клиентов. На этом правиле строится таргетированная реклама, которая показывается только целевой аудитории, то есть 20% общего числа потенциальных клиентов;
• большую часть функций выполняет малая доля работников. Выгодно повысить зарплату на самых важных должностях и перевести менее важные задачи на других рабочих.

Принцип Парето отлично работает в учёбе: вам нужно сделать всего 20% усилий, с остальным разберётся Феникс.Хэлп.