Как складывать матрицы различного порядка
Мы уже знаем, что матрица – это объект, который представляет собой совокупность взаимосвязанных строк (m) и столбцов (n). С ней можно проводить различные действия, от обычного вычитания до транспортирования. Разберёмся с самой простой матричной операцией – сложением.
Сложение матриц — теория
Сложение матриц – это алгоритм вычисления новой матрицы С при помощи попарного суммирования соответствующих элементов матриц А и В.
Формула:
\(с_{ij} = a_{ij} + b_{ij}\)
где i – номер строки, а j – номер столбца.
То есть, чтобы получить, например, элемент \(с_{11}\), нужно сложить \(а_{11}\) и \(b_{11}\).
Когда это возможно, можно ли складывать матрицы разной размерности
Как сложение, так и вычитание матриц возможно только в том случае, когда они равны по размеру.
Также подметим, что нельзя складывать матрицы с обычными целыми числами и дробями. Порядок элементов в таблице менять нельзя.
Экономический смысл сложения матриц
Матрица имеет прикладное значение, так как часто используется в экономике для систематизации информации и облегчения вычислений. К примеру, с помощью неё можно предоставить отчёт о продажах:
Пусть \(х_{ij}\) – это количество определённого товара, проданного в определённом магазине за первый год. Матрица У – отчёт о продажах за второй год. Тогда, чтобы посчитать сумму продаж за оба года, нужно сложить отчёты Х и У.
Свойства операции сложения матриц
Свойств немного, и все они легки для запоминания:
- Свойство коммутативности: A+ B = B + A.
- Свойство ассоциативности: (A+ B) + C= A + (B + C).
- Свойство дистрибутивности: (A+ B) * C= AC + BC.
При сложении А с нулевой матрицей 0, у которой все элементы равны нулю, исходная матрица не меняется:
А + О = А
При сложении А с противоположной матрицей (-А) сумма равна нулю:
А + (-А) = О
Примеры с решением на нахождение суммы матриц
Задача №1
Даны слагаемые:
Найти: С
Решение
\(с_{11} = а_{11} + б_{11} = 2 + 1 = 3\)
\(с_{12} = а_{12} + б_{12} = 3 + (-3) = 0\)
\(с_{21} = а_{21} + б_{21} = (-1) + 2 = 1\)
\(с_{22} = а_{22} + б_{22} = 4 + 5 = 9\)
Ответ:
Задача №2
Даны слагаемые:
Найти: С
Решение: так как матрицы разного размера (А = 2 × 3; В = 3 × 2), данная операция невозможна.
Ответ: нет решения.
Не справляетесь с заданиями по учебе? Обращайтесь в ФениксХелп за помощью!
Понравилась статья?
Подпишитесь на наш блог и получайте наши статьи первым!
Или подписывайтесь на нас в соцсетях:
Заметили ошибку? Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так

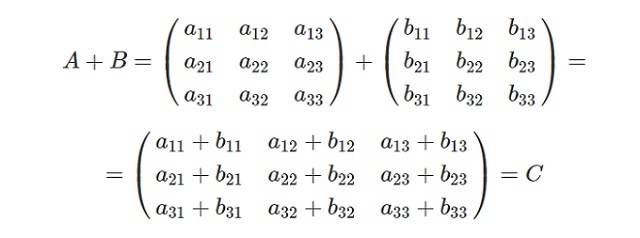





Бесплатно отвечаем на ваши вопросы. Задайте свой вопрос и получите ответ от профессионального преподавателя. Выберите лучший ответ.
Вопросы могут задавать только авторизованные пользователи. Войти