Диагональные матрицы: определение и свойства
Матрица — это прямоугольная таблица чисел, состоящая из определенного количества строк и столбцов. Существует множество матричных видов, и один из них — диагональный. Разберемся, что он из себя представляет.
Что такое диагональная матрица
У диагональной матрицы элементы, расположенные вне главной диагонали, равны нулю.
Напомним, что матрица считается квадратной, если количество строк равно количеству столбцов (m = n).
Особенности и свойства
Для начала нужно понять, что такое матричный определитель.
Определитель (детерминант) — это некоторая величина, с которой можно сопоставить любую квадратную матрицу.
Определитель А = (2×2), к примеру, вычисляется по формуле:
Из этого следует свойство №1: определитель диагональной матрицы равен произведению ее диагональных элементов.
Свойство №2: обратная матрица для диагональной равна:
Свойство №3: ранг равен количеству ненулевых диагональных элементов.
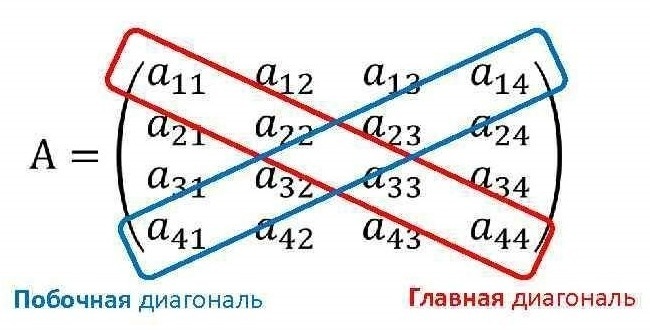
Главная и побочная диагонали
Главную диагональ образуют элементы, расположенные на местах \(а_{11}\), \(а_{22}\), \(а_{33}\)…\(а_{NN}\). Их соответственно называют диагональными.
Побочной диагональю называют диагональ элементов от правого верхнего угла до нижнего левого. Эти диагонали параллельны друг другу.
Частные случаи диагональных матриц
Существуют три основных подвида: единичная, нулевая, скалярная.
Единичная матрица
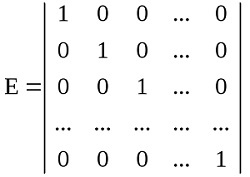
У единичной матрицы все диагональные элементы равны единице.
В формулах ее обозначают буквой Е.
Нулевая матрица
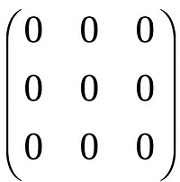
В нулевой матрице все элементы, в том числе диагональные, равны нулю.
В формулах ее обозначают цифрой 0.
Скалярная матрица
В скалярной матрице все элементы на главной диагонали равны друг другу.
В некоторых случаях говорят, что скалярная матрица — это произведение скаляра на единичную матрицу Е. В ней диагональные элементы могут быть как положительными, так и отрицательными.
Примеры решения диагональных матриц
Иногда недиагональная матрица может быть приведена к диагональному виду.
Условие: дана матрица А
Задача: привести к диагональному виду.
Решение: характеристическое уравнение равно
а его корни: \(λ_1 = 5\), \(λ_2 = (-2)\)
Если \(λ_1 = 5\), то
Пусть \(х_2 = с\), тогда вектор равен:
Если \(x = λ_2 = (-2)\), то
Пусть \(х_2 = с\), тогда вектор равен:
Таким образом, диагональная матрица имеет вид:
Изучение данных математических объектов имеет свои подводные камни. Если у вас нет времени на учебу, Феникс.Хелп может помочь вам с решением контрольных, самостоятельных и иных проверочных работ.
Понравилась статья?
Подпишитесь на наш блог и получайте наши статьи первым!
Или подписывайтесь на нас в соцсетях:
Заметили ошибку? Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так

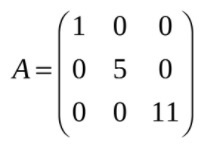
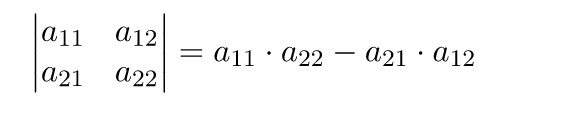
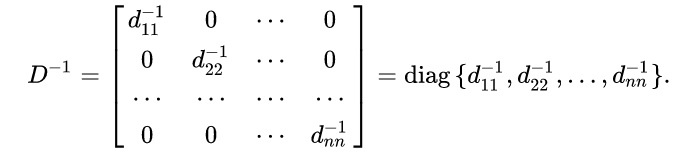

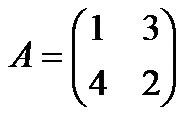
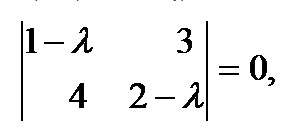
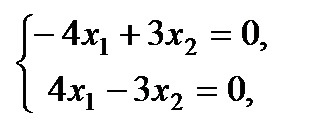
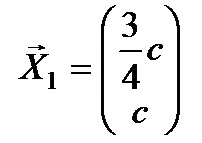
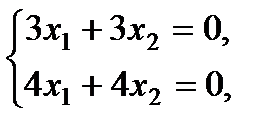
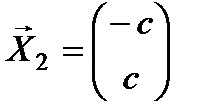
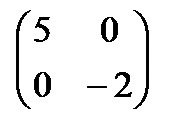
Бесплатно отвечаем на ваши вопросы. Задайте свой вопрос и получите ответ от профессионального преподавателя. Выберите лучший ответ.
Вопросы могут задавать только авторизованные пользователи. Войти