Что называется числовой последовательностью

С числовыми последовательностями человек сталкивается постоянно. Ранее русские математики оперировали термином вариант, который ввел Ш. Мерэ. Последовательность включает ряд чисел. Данный объект является одним из ключевых понятий в математическом анализе.

Что такое числовая последовательность — понятие и определение

Последовательность обладает рядом отличительных признаков:

• каждый элемент из множества соотносится с натуральным числом;
• число используют для обозначения номера элемента и идентификации позиции этого компонента в рассматриваемой последовательности;
• для всех элементов можно определить следующий за ним компонент последовательности.

Предположим, что х является числовым множеством. Тогда можно использовать его в формулировке числовой функции.

Множество х в данном случае представляет собой область определения.

С помощью функции можно определить любой член из последовательности. Этим свойством она отличается от произвольного комплекса чисел. В математике принято использовать буквы и числа для записи понятий и законов. Числовые последовательности, как правило, обозначают буквой х, хотя строгих правил на этот счет не предусмотрено.

\(x_{n}=f\left(n \right)\)

\(x_{1},x_{2},x_{3},x_{4},...x_{n},...\)

В число самых интересных и популярных числовых последовательностей входит последовательность Фибоначчи. Она обладает удивительными свойствами и нередко наблюдается в природном мире. К примеру, семена подсолнечника расположены в порядке, который имеет форму спирали. Числа, с помощью которых обозначают количество семян в каждой из них, представляют собой члены последовательности Фибоначчи.

Какие бывают последовательности чисел

Данное понятие может быть представлено в разных видах. Среди числовых последовательностей различают следующие формы:

• постоянная или монотонная, имеет вид: 1, 1, 1, 1, 1 …;
• возрастающая характеризуется признаком, согласно которому каждый последующий компонент будет больше предыдущего;
• убывающая, в которой каждый следующий элемент меньше предыдущего.

Кроме стандартной классификации, числовые последовательности подразделяют на следующие категории:

• сходящиеся, с конечным пределом;
• расходящиеся, в которых предел соответствует бесконечности, либо вообще отсутствует.

Наиболее распространенными примерами последовательностей являются те, которые проходят на школьных уроках. К ним относят арифметическую и геометрическую прогрессию.

Арифметическая прогрессия

Раскрыть данное понятие поможет последовательность чисел:

1, 3, 5, 7, 9, 11, 13, 15…

a₁, a₂, a₃, a₄, a₅, a₆, a₇, a₈... a_n,...

Следует отметить, что данные числа являются нечетными. Каждый следующий элемент можно вычислить, если прибавить к нему одно и то же число. Пусть данное число будет записано, как d. В данном примере d = 2.

Представленная последовательность является арифметической прогрессией. Для этого вида числового ряда справедлива формула:

\(a_{n+1}=a_{n}+d\)

Элемент а, которому соответствует номер n, является общим членом последовательности. Число d представляет собой разность арифметической прогрессии.

\(a_{n}=a_{1}+d(n-1)\)

\(d=a_{n+1}-a_{n}\)

Сумму первых n компонентов последовательности можно рассчитать с помощью уравнения:

\(S_{n}=\frac{a_{1}+a_{n}}{2}n\)

Ряд свойств характерен для арифметической прогрессии:

\(a_{n}=\frac{a_{n+1}+a_{n-1}}{2}\)

Геометрическая прогрессия

Данное определение соответствует последовательности чисел, состоящей из элементов, каждый из которых, начиная со второго, равен предыдущему члену, умноженному на одно и то же число q. Данное число является знаменателем прогрессии. Для компонентов геометрической прогрессии справедливо выражение:

\(b_{n+1}=b_{1}\times q^{n}\)

При рассмотрении геометрических прогрессий используют основные формулы. Для расчета n-го элемента прогрессии следует воспользоваться уравнением:

\(b_{n}=b_{1}\times q^{n-1}\)

Определить сумму первых n членов последовательности можно таким образом:

если \(q\neq 1\)

то \(S_{n}=\frac{b_{1}(q^{n}-1)}{q-1}\)

если \(\left| q\right|< 1\)

то \(S_{n}=\frac{b_{1}}{q-1}\)

Характеристическим свойством геометрической прогрессии является следующее равенство:

\(b^{2}_{n}=b_{n-1}\times b_{n+1}\)

Предел последовательности, основные свойства

Согласно определению, последовательность является некоторой функцией. Поэтому определение пределов последовательностей во многом сходится с вычислением пределов функций, но обладает некоторыми особенностями.

По-другому, предел последовательности представляет собой число, в окрестности которого расположены все компоненты последовательности, начиная с определенного. Переменная n в данном случае всегда будет стремиться к бесконечности, в сторону увеличения натуральных чисел.

Способы задания числовых последовательностей

Такие действия можно выполнять по-разному. К основным способам задания последовательностей относят:

• аналитический или с помощью формулы;
• реккурентный, при наличии нескольких известных первых элементов прогрессии и формулы для определения следующих членов последовательности;
• описательный, включает простое перечисление всех компонентов последовательности.

Аналитический способ задания числовой последовательности

Считают, что последовательность задана аналитически, когда представлено уравнение для расчета ее n-го элемента.

\(y_{n}=f(n)\)

В качестве примера можно рассмотреть:

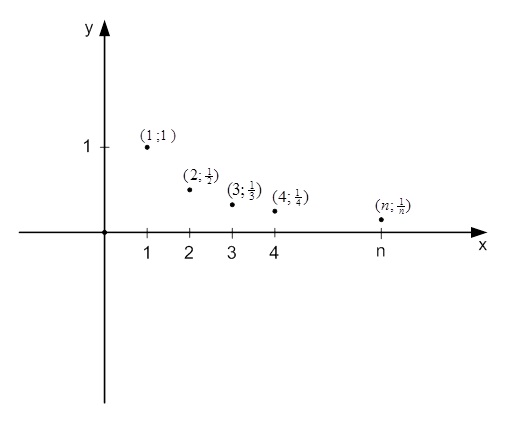
\(y_{n}=\frac{1}{n}\)

Это аналитический способ задания последовательности чисел:

\(1;\frac{1}{2};\frac{1}{3};...\frac{1}{n};...\)

Зная конкретное значение n, можно определить элемент последовательности с соответствующим номером. Можно изобразить данную последовательность на графике. Исходя из определения графика функции, он будет представлять собой множество всех точек:

\((n;\frac{1}{n})\)

Указанные точки будут расположены на правой ветви гиперболы:

\(y=\frac{1}{x}\)

Функция  \(y=\frac{1}{x}\) в случае, когда x > 0, будет убывающей. В таком случае числовая последовательность \(y_{n}=\frac{1}{n}\) также будет убывать.

Можно рассмотреть второй пример, когда:

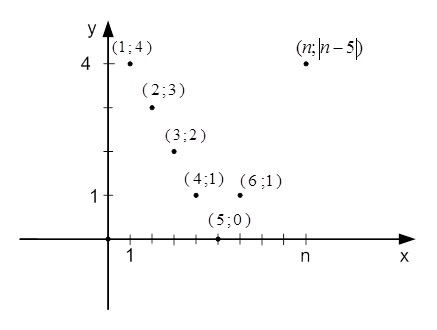
\(y_{n}=\left|n-5 \right|\)

Следует представить несколько элементов данной числовой прогрессии:

\(y_{1}=\left|1-5 \right|=4\)

\(y_{2}=\left|2-5 \right|=3\)

\(y_{3}=\left|3-5 \right|=2\)

Графиком рассматриваемой последовательности будет являться множество точек, которые характеризуются координатами:

\((n;\left|n-5 \right|)\)

Эти точки принадлежат ломаной линии:

\(y=\left|x-5 \right|\)

Числовая последовательность \(y_{n}=\left|n-5 \right|\) будет убывать, если n соответствует интервалу от 1 до 5, и возрастать – при n от 5 до бесконечности.

Описательный метод задания числовой последовательности

Данная методика используется не всегда. Описательный способ записи последовательности чисел целесообразно применять, когда в условии задачи отсутствуют формулы, а правило прогрессии изложено лишь словами. В качестве примера можно рассмотреть такую последовательность, в которой:

\(a_{n}\) является цифрой после запятой в десятичной записи числа \(\sqrt{2}\)

\(\sqrt{2}=1,41421…\)

\(a_{1}=4\); \(a_{2}=1\);\(a_{3}=4\);\(a_{4}=2\);\(a_{5}=1\);…

Рекуррентный способ задания числовой последовательности

Рекуррентной называют последовательность, в правилах которой указано, что для расчета n-го члена необходимо знать значение предыдущих. В качестве примера можно привести такие условия:

\(y_{1}=1\)

\(y_{2}=1\)

\(y_{n}=y_{n-2}+y_{n-1}\)

\(n = 3, 4, 5 …\)

Данный пример демонстрирует возможность рассчитать любой n-ый элемент числовой последовательности.

Действия над числовыми последовательностями

Представленные формулы позволяют производить разнообразные манипуляции с рядом чисел. К основным действиям относятся:

1. Суммировать последовательности x_n и y_n в виде последовательности x_n + y_n с элементами x₁+y₁  x₂+y₂  x₃+y₃  … x_n+y_n.
2. Найти разность последовательностей x_n и y_n в виде последовательности x_n - y_n с элементами x₁-y₁  x₂-y₂  x₃-y₃  … x_n-y_n.
3. Умножение последовательностей x_n и y_n в виде последовательности x_n * y_n с элементами x₁*y₁  x₂*y₂  x₃*y₃  … x_n*y_n.
4. Поиск частного последовательностей x_n и y_n в виде последовательности x_n / y_n с элементами x₁/y₁  x₂/y₂  x₃/y₃  … x_n/y_n.

При выполнении расчетов и решении задач с последовательностью чисел следует учитывать важные особенности:

• последовательность может обладать только одним пределом;
• последовательность с пределом считается ограниченной, обратное утверждение не всегда справедливо;
• в случае, когда элементы какой-либо последовательности z_n находятся между соответствующими компонентами пары последовательностей x_n и y_n сходящихся к одному пределу, то и эта последовательность сходится к тому же пределу;
• предел постоянной числовой прогрессии соответствует ее постоянному;
• равные между собой числовые последовательности x и y обладают равными друг другу пределами при их наличии;
• в ситуации, когда каждый элемент сходящейся последовательности не превосходит соответствующего элемента другой сходящейся последовательности, то и предел первой не превосходит предела второй;
• предел суммы или разности пары числовых прогрессий соответствует сумме или разности их пределов в случае, когда рассматриваемые последовательности обладают пределами;
• предел произведения пары числовых прогрессий, для которых характерно наличие пределов, имеет место быть и рассчитывается, как произведение пределов последовательностей;
• при работе с постоянным множителем допускается выносить его за знак предела;
• предел частного пары числовых прогрессий, обладающих пределами, равен частному пределов этих последовательностей, если предел знаменателя не равен нулю.

Примеры задач с решением

Задача 1

Дана числовая последовательность

\(y_1=1\)

\(y_2=1\)

\(y_n=y_{n-2}+y_{n-1}\)

\(n = 3, 4, 5 …\)

Требуется найти 7-ой элемент последовательности.

Решение

Для определения 7 члена числовой последовательности следует узнать 5 и 6 компоненты.

\(y_4=3\)

\(y_5=5\)

\(y_6=3+5=8\)

\(y_7=5+8=13\)

Ответ: 7 член равен 13.

Задача 2

По условию задачи

\(x_{n}=\frac{n-1}{2n+1}\)

Требуется найти \(x_{3}\)

Решение

В начало необходимо подставить n=3 в уравнение для определения n-го элемента последовательности:

\(x_{n}=\frac{n-1}{2n+1}\)

Формула будет преобразована таким образом:

\(x_{3}=\frac{3-1}{2*3+1}=\frac{2}{7}\)

Ответ: \(x_{3}=\frac{2}{7}\)

Задача 3

Дана формула для определения n-го компонента прогрессии:

\(x_{n}=\frac{n-1}{2n+1}\)

Требуется выяснить, является ли число \(\frac{4}{11}\) каким-либо из элементов рассматриваемой последовательности.

Решение

Следует приравнять уравнение для n-го компонента последовательности \(x_{n}=\frac{n-1}{2n+1}\) к указанному в условии задачи числу \(\frac{4}{11}\) для получения уравнения относительно n. В том случае, когда n представляет собой натуральное число, то число \(\frac{4}{11}\) будет являться членом заданной прогрессии.

\(\frac{n-1}{2n+1}=\frac{4}{11}\)

\(11n – 11 = 8n + 4\)

\(3n = 15\)

\(n = 5\)

Ответ: число \(\frac{4}{11}\) является 5 членом последовательности.

Задача 4

Требуется записать уравнение общего члена последовательности, которая задана несколькими компонентами: 1, 4, 9, 16, 25.

Решение

Сначала необходимо записать каждый из членов прогрессии в таком виде:

\(y_{1}=1=1^{2}\)

\(y_{2}=4=2^{2}\)

\(y_{3}=9=3^{2}\)

\(y_{4}=16=4^{2}\)

\(y_{5}=25=5^{2}\)

Следует отметить, что компоненты прогрессии являются квадратами последовательных натуральных чисел. Согласно этому утверждению, можно сделать следующий вывод:

\(y_{n}=n^{2}\)

Ответ: \(y_{n}=n^{2}\)

Числовые последовательности исследовались многими математиками с мировым именем на протяжении веков. Зная основные формулы и правила работы с прогрессиями, можно достаточно просто решать задачи с рядами чисел и определять компоненты последовательностей. Если в процессе освоения какой-либо темы возникают сложности, можно обратиться за помощью к сервису Феникс.Хелп.