Правило умножения матриц: примеры с решением
Мы помним, что матрицы – это таблицы взаимосвязанных элементов, которые позволяют упростить математические вычисления и систематизировать определённую информацию. Их можно складывать, вычитать, умножать между собой. В этой статье подробнее остановимся на последнем алгоритме – матричном произведении.
Умножение матриц — определение
Матричное умножение – это одна из основных операций, которая проводится исключительно с согласованными матрицами.
При произведении матриц A и B получается новая матрица C. В математическом виде формула будет выглядеть так:
Но для начала разберёмся, что такое согласованные матрицы.
Согласованные матрицы
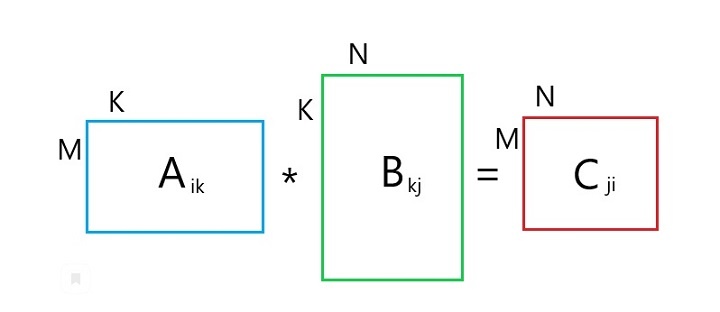
Согласованными матрицами называют матрицы вида A = [m ☓ n] и B = [n ☓ k], где количество столбцов А равно количеству строк В.
Индексы показывают координаты равных элементов.
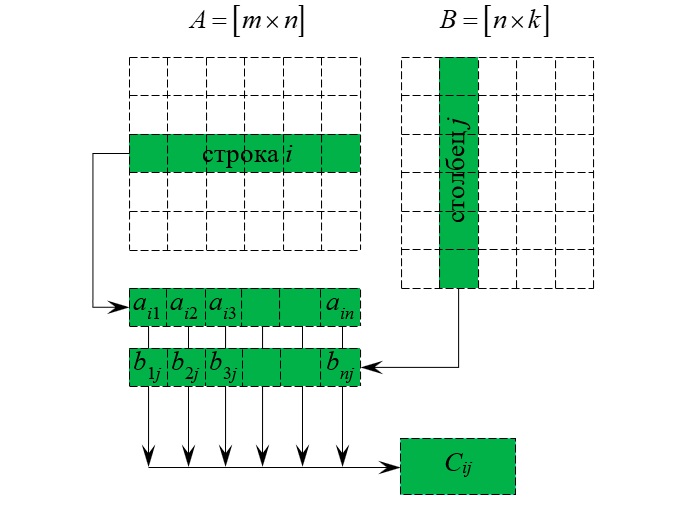
Для того, чтобы умножить А и В, нужно взять строку в первой матрице и столбец во второй, перемножить одинаковые элементы и сложить полученные произведения.
Основные свойства матричного произведения
Размеры, то есть количество строк (m) и столбцов (n), влияют на особенности матричного произведения. Следовательно, для двух главных видов – квадратных и прямоугольных – действуют разные свойства произведения. Однако умножение любого вида всегда некоммуникативное. Это означает, что матрицы нельзя менять местами (АВ ≠ ВА).
Умножение квадратных матриц
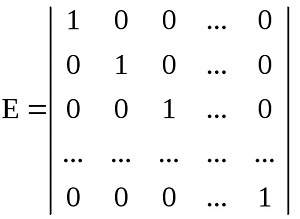
Для квадратных матриц существует единичная матрица Е. В ней элементы по главной диагонали равны единице, а оставшиеся – нулю. Произведение любой квадратной матрицы на неё не влияет на результат.
В математическом виде это выглядит так: ЕА = АЕ = А
Также существует обратная матрица А (-1), при умножении на которую исходная A = [m ☓ n] даёт в результате единичную матрицу E.
Следовательно, формула такова: АА(-1) = Е
Умножение прямоугольных матриц
Существуют четыре основных свойства умножения:
- Сочетательное свойство, или ассоциативность: (AB)C = A(BC)
- Распределительное свойство, или дистрибутивность: А(В+С) = АВ + АС / (А+В)С = АС + ВС
- Умножение на единичную матрицу: ЕА = А
- Умножение на нулевую матрицу: 0А = 0
Напомним, что у нулевой матрицы все элементы равны нулю.
Произведение трех матриц
Произведение АВС можно получить двумя альтернативными способами:
- Найти АВ и умножить на С
- Найти ВС и умножить на А
(АВ) С = А (ВС)
Данное свойство называется ассоциативностью матричного умножения и действует на все виды согласованных матриц. Сами они не переставляются, меняется только порядок их умножения.
Умножение матрицы на число
Для умножения на число необходимо умножить каждый матричный элемент на это число:
Дроби вносить не нужно, поскольку они могут затруднить дальнейшие операции.
Умножение матрицы на вектор
Здесь работает правило «строка на столбец».
При умножении на вектор-столбец важно, чтобы количество столбцов в матрице совпадало с количеством строк в векторе-столбце. Результатом произведения будет вектор-столбец.
При умножении на вектор-строку матрица должна быть только вектором-столбцом. Важно, чтобы количество строк в векторе-столбце совпадало с количеством столбцов в векторе-строке. Результатом произведения будет квадратная матрица.
Примеры задач на умножение матриц
Задача №1: выполнить умножение и найти С, если A = [m ☓ n] и B = [n ☓ k] равны.
Решение:
c11 = a11·b11 + a12·b21 = 4·3 + 2·(-3) = 12 - 6 = 6
c12 = a11·b12 + a12·b22 = 4·1 + 2·4 = 4 + 8 = 12
c21 = a21·b11 + a22·b21 = 9·3 + 0·(-3) = 27 + 0 = 27
c22 = a21·b12 + a22·b22 = 9·1 + 0·4 = 9 + 0 = 9
Ответ:
Задача №2: вычислить С, если А = [m ☓ n] и вектор-столбец В равны.
Решение:
c11 = a11·b11 + a12·b21 = 2·1 + (-1)·2 + 3·(-1) = -3
c21 = a11·b12 + a12·b22 = 4⋅1 + 2⋅2 + 0⋅2 = 8
c31 = a21·b11 + a22·b21 = −1⋅1 + 1⋅2 + 1⋅(−1) = 0
Ответ:
Изучение матричных операций очень увлекательное, но сложное занятие. Если у вас нет времени на учёбу, ФениксХэлп может помочь в решении контрольных и самостоятельных работ, написании статей и диссертаций.
Понравилась статья?
Подпишитесь на наш блог и получайте наши статьи первым!
Или подписывайтесь на нас в соцсетях:
Заметили ошибку? Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так

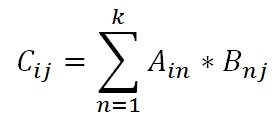
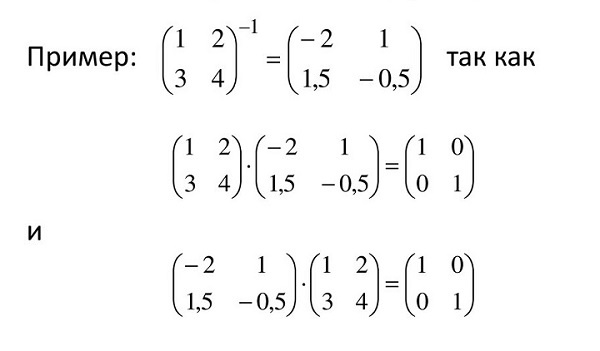

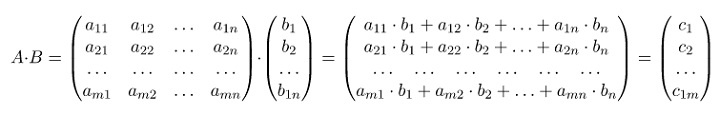
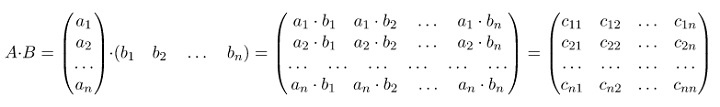
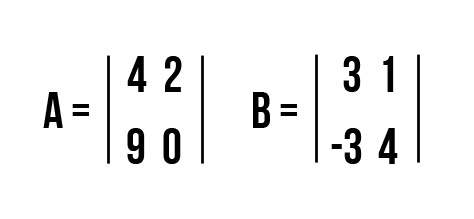
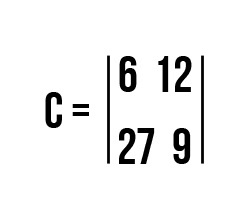
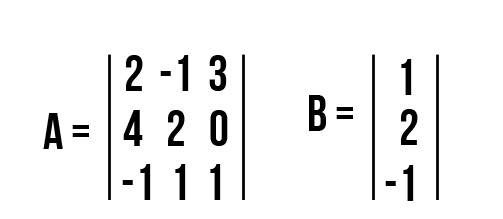
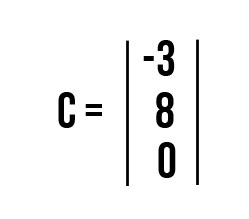
Бесплатно отвечаем на ваши вопросы. Задайте свой вопрос и получите ответ от профессионального преподавателя. Выберите лучший ответ.
Вопросы могут задавать только авторизованные пользователи. Войти