Математические лайфхаки: как научиться быстро считать в уме

Сегодня говорим о том, как научиться быстро считать в уме и как это поможет решать сложные примеры и задачи. Вы спросите, зачем это нужно, если в каждом телефоне есть функция калькулятора. Хотя бы для того,  чтобы оперативно посчитать сумму чека и быть уверенным, что вас не обманул продавец при покупке килограмма конфет или печенья.  

После освоения правил устного счета у вас не будет возникать мысли считать на калькуляторе. Гораздо быстрее будет сделать все подсчеты в уме. Это и мозг потренирует, и впечатление на окружающих произведет.

Чтобы развить навыки устного счета, нужно практиковаться, удерживать в памяти числа и помнить основные формулы. Вначале считать будет достаточно сложно. Но в процессе тренировок вы научитесь быстро концентрироваться и производить расчеты в считанные секунды.

В истории математической науки есть ученые, обладающие поразительной скоростью устного счета. Среди них — Карл Фридрих Гаусс. По его словам, сначала он научился считать, а потом уже говорить. В три года мальчик взял в руки платежную ведомость отца, просмотрел ее и заявил, что в расчетах ошибка. Взрослым пришлось перепроверить документ. Оказалось, маленький Карл Гаусс был прав. В своей жизни математик достиг многого. Его труды до сих пор актуальны. До самой смерти Гаусс производил большинство вычислений в уме. 

Складываем в уме

Практику устного счета лучше начинать с самого простого: изучения состава числа от 1 до 10. Когда нужно найти сумму односложных слагаемых, вопросов обычно не возникает. Чаще всего проблемы начинаются, когда число при сложении переходит через разряд. Чтобы избежать таких ошибок, удобно использовать метод «опоры на десяток». 

Нужно вспомнить состав числа и мысленно определить, сколько не хватает до 10 одному из слагаемых, а затем прибавить оставшуюся часть к 10. 
Разберем способ на примере. Допустим надо сложить 6 и 7. Чтобы получить 10, первому слагаемому не хватает 4 (4=7-3). Остаток прибавляем к 10: 3=7-4. В итоге получаем 13.

Основной принцип со сложением больших чисел — деление их на разрядные части, а затем сложение этих частей. Вернемся к практике. Допустим, нам необходимо сложить 456 и 365. Разбиваем оба эти числа на разряды: 400+50+6 и 300+60+5 соответственно. А теперь производим сложение. Считаем, (400+300)+(50+60)+(6+5) = 700+110+11=810+11=821.

Вычитаем в уме

Вычитание — это математическое действие, когда от большого числа отнимается меньшее. Метод «опоры на десяток» здесь также актуален. С единственным отличием: на разряды нам нужно разбить только вычитаемое. Разберем пример: из 748 вычитаем 312. Вычитаемое — 312. Разбиваем его на разряды и получаем: 300+10+2. Теперь производим расчет: 748-300-10-2=448-10-2=478-2=476.

Современных младших школьников учат визуализировать числовой ряд и производить расчеты слева направо. Такой способ быстрее и удобнее, чем вертикальный, где считают сверху вниз (проводят расчет столбиком).  

Умножаем в уме

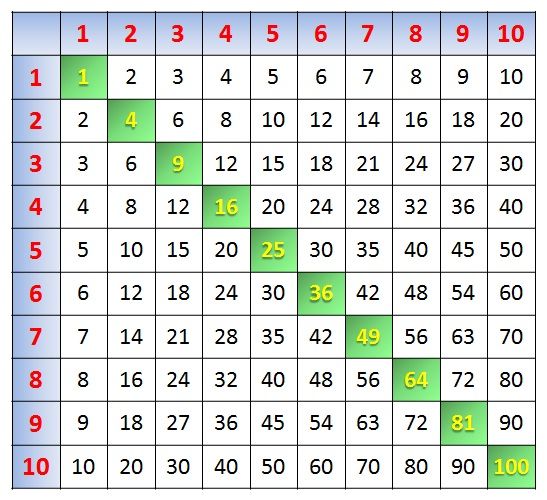
Умножение —  это действие, при котором из двух чисел первое повторяется столько раз, сколько показывает второе. Решить примеры, где оба множителя простые, не составит труда даже школьнику. Инструмент, который помогает справиться с такими примерами, известен как таблица умножения. Настоятельно рекомендуем повторить ее, прежде чем браться за практику устного счета.

1. Умножение многозначных чисел на однозначные. Вспоминаем метод «опоры на десяток». Первый множитель — сложное число— разбиваем на разряды, каждый из которых умножаем на второй множитель. А затем суммируем полученные результаты. Например, требуется 467 умножить на 5. Переходим к вычислениям: 467*5=(400+60+7)*5=(400*5)+(60*5)+(7*5)=2000+300+35= 2335.
2. Умножение двузначных чисел. Все то же самое, только с большей загрузкой памяти. Умножаем 28 на 35. Второй множитель разделяем на разряды: 28*(30+5)=(28*30)+(28*5)=(20*30+8*30)+(20*5+8*5)=600+240+100+40=980. Другой пример, где 56 надо умножить на 37. Это значит, что 56 нужно «взять» 37 раз. 
3. Умножение на 11. Для решения примера надо два составляющих первого множителя сложить друг с другом, а затем вписать сумму между ними. В ответе будет трехзначное число. Например, разберем пример 15 умножить на 11. Действуем по озвученному алгоритму: 1+5=6; 15*11=165.
4. Возведение числа в квадрат. Возведение в квадрат — это умножение числа само себя. Делимся приемом, который позволит произвести это действие быстро с двузначными числами. Результат вычисления начинается с произведения (умножения) первой цифры числа на следующее за ней по иерархии(n, n+1) и заканчивается квадратом последней (умножением саму на себя). Рассмотрим пример: 652=6*7 и 5*5= 4225.

Делим в уме

Мы на финишной прямой! Итак, деление — это действие, обратное умножению.

1. Деление на однозначное число. Если делитель (на которое делят) — однозначное число, то из делимого (которое делят) необходимо выделить часть (максимально большую), которую можно без труда разделить с помощью таблицы Пифагора. Например, 6144 надо разделить на 6. Упрощаем нашу задачу: 6144:6=(6000+144):6=1000+144:6=1000+(120+24):6=1000+20+4=1024
2. Деление на двузначное число. Здесь можно использовать технику «подбора». Обратите внимание на последнюю цифру составного числа. При умножении двух многозначных чисел последняя цифра произведения будет совпадать с последней цифрой результата умножения последних цифр этих чисел. Итак, у нас есть пример:  5586:42. Необходимо определить число, которое при умножении на 42 даст 5586. Используем метод подбора, но прежде анализируем. Произведение чисел 42 и — 4200. 5586-4200=1386. В числе «4200» 1386 может повториться не более 3 раз. Делимое 5586 заканчивается на 6. А делитель — на 2. Значит, на конце частного будет 3. Собираем все данные в кучу и получаем предполагаемое частное 133. То есть, 5586:42=133

Вуаля! Решение найдено.

Организуем себе тренировки

Мы разобрались со всеми математическими действиями. Пора приступать к тренировкам. Возникает резонный вопрос, где брать тренировки? Ответ прост. На сегодняшний день существует множество приложений для смартфона, которые предложат попрактиковать навыки устного счета. При выборе обратите внимание на настройки сложности, возможность программы собирать статистику.

Полезные советы

Подведем итог и приведем несколько полезных рекомендаций:

• практикуйтесь ежедневно, и успех не заставит себя ждать;
• не бросайте тренировки в случае первой неудачи;
• используйте различные методики счета, изучайте литературу по теме.

Устный счет развивает память, внимание, умение выполнять несколько задач одновременно и быстро переключаться между процессами. А сколько времени это умение сэкономит на важных контрольных работах! Ну а если что-то не выходит — не расстраивайтесь, а срочно звоните в Феникс.Хелп – там помогут решить проблемы с учебой.