Решение задач на силу упругости

Любое тело перестает падать вниз, если его подвесить на крепкий шнурок. На него по-прежнему действует сила тяжести. Но она уравновешивается еще одной величиной – силой упругости шнурка. Как она действует на тело, что нужно для ее преодоления, — вопросы, ответы на которые найдете в материале.

Что такое сила упругости

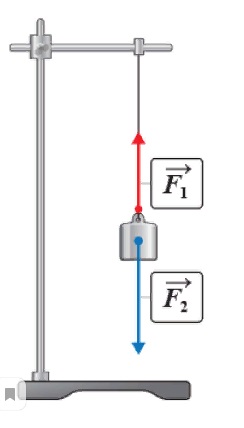
Любое тело, совершающее заданный полет, в конце концов падает на землю под действием собственной силы тяжести. Исключение составляют предметы, подвешенные кверху либо располагающиеся на опоре. Их падение становится невозможным, поскольку силу тяжести компенсирует упругость подвеса. Опытным путем еще в школьной программе демонстрируется момент: когда две силы равны, предмет «замирает» в воздухе. При этом их направления действия строго противоположны. Явление, препятствующее падению подвешенных либо размещенных на опоре предметов, обусловлено проявлением силы упругости.

Чем сильнее растягивается нить, на которой подвешен предмет, и чем больше прогибается доска под грузом, тем значительнее сила упругости, которая в них возникает.

Нить стремится растягиваться до тех пор, пока две величины не уравновесятся.

Растяжение нити аналогично, например, следующим явлениям:

• изменению формы мяча при ударе по нему ногой (начинает действовать сила сжатия);
• противостоянию каната при закручивании его вокруг своей оси (сила кручения);
• сдвиганию частей одного предмета друг относительно друга (сила сдвига);
• сложностям согнуть прут в дугу или окружность (сила кручения).

Во всех случаях внешней силе, действующей в определенном направлении, начинает препятствовать другая величина, направленная противоположно и стремящаяся компенсировать ее абсолютное значение.

К такому выводу впервые пришел английский ученый Роберт Гук в 1660 году, отметив, что интенсивность изменения длины тел при их растягивании прямо пропорционально зависит от значения силы упругости.

Его открытие приобрело статус закона Гука, формула которого выглядит следующим образом:

\(Fупр=k*Δl\)

\(k\) – коэффициент пропорциональности, имеющий специальное название «жесткость»;

\(Δl\) – величина, характеризующая изменение длины тела.

K зависит от свойств материала изготовления тела, его параметров и форм.

Выражение закона Гука возможно и через другую формулу:

\(\xi\;=\;x⁄l\)

где \(\xi\;\) — относительная деформация, 

\(\sigma=F⁄S\)

где \(\sigma\) — напряжение, возникающее в материале,

\(S\) — площадь поперечного сечения тела,

\(\varepsilon=1⁄E\sigma\)

В каких условиях применяется закон Гука

Универсальным вариантом для применения закона Гука является тонкий стержень. \(F\) в данном случае выражает ту силу, которая к нему прилагается. Зависит она от разницы длины до и после воздействия, а также коэффициента упругости материала.

\(F=k\ast\Delta l\)

Как было сказано выше, \(k\) зависит от качества материала и габаритов. Выражая названую зависимость через площадь сечения и длину, формула для коэффициента получает следующий вид: \(F=ES/L\). Буквой \(Е\) здесь обозначается все тот же модуль Юнга – механические свойства материала. Далее следует ввести понятия относительного удлинения:

\(\xi=\Delta l/L\)

и напряжения в поперечном сечении:

\(\sigma=F/S\)

Конечная формула закона Гука может выглядеть и так:

\(\triangle l=FL/ES\)

Для понимания того, какие условия необходимы для функционирования закона Гука, достаточно рассмотреть два понятия: среда и сила. В таких средах, как газы, жидкости, особенно вязкие, механические особенности процессов упругости не действуют. В то же время даже очень интенсивная сила не будет работать в ряде сред.

Обязательные условия для ее проявления:

1. Незначительные изменения формы.
2. Достаточная упругость материала.
3. В материале ни при каком воздействии не происходит изменений линейного характера.

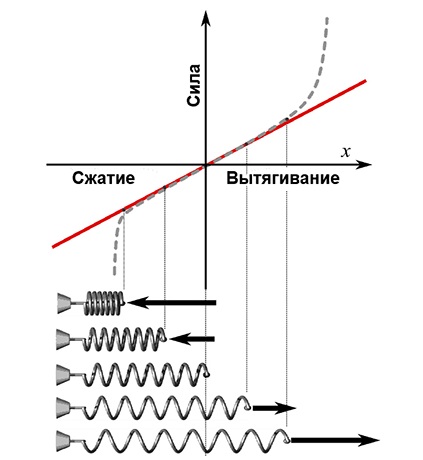
Рассмотрим график, отражающий зависимости:

Нижний левый квадрат демонстрирует линейную зависимость при не интенсивных растяжениях. Затем пунктирная линия демонстрирует потерю этой «линейности». Визуально это проявляется «непослушанием» пружины: она перестает принимать свой первоначальный вид при интенсивном растяжении. Если его вовсе не прекращать, может нарушиться природная структура материала, произойдет полный излом.

Аналогичная картина наблюдается при процессе сжатия. В правом верхнем квадрате отражены следующие особенности:

При небольшом сжатии – связь прямая (красная линия).

При увеличении силы зависимость теряет «линейность» — см. пунктир.

Сильное сжатие заставляет пружину нагреваться, она теряет первичные свойства. Происходит слипание витков и разрушение структуры материала.

Примеры решения задач на силу упругости

 Задания по определению силы упругости часто встречаются в экзаменационных работах и олимпиадах.

Задача 1

Для растяжения пружины прикладывают силу 30 Н (F₁). Тогда ее длина составляет 28 см. При ее сжатии с такой же F₂, длина уменьшается до 22 см. Найти начальную длину пружины, а также коэффициент ее жесткости.

Решать задачу следует по схеме:

\(F1=k(l1-l0)\)

\(F2=k(l0-l2)\)

Из этих формул вытекает: \(l1-l0=l0-l2\)

\(l0=(l1+l2)/2=(28+22)/2=25\)

Определение жесткости пружины нужно произвести по формуле:

\(k=F1/(l1-l0)=30/(28-25)*10^{-2 }=1000\)

Ответ: 25 см, 1000 Н/м

Задача 2

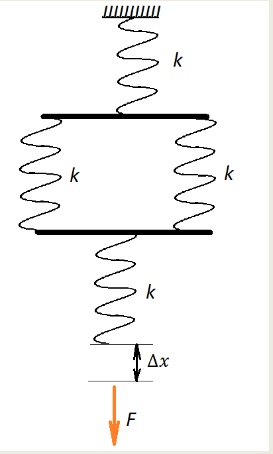
Пружины соединены способом, изображенным на схеме:

Жесткость каждой составляет 10 Н/м. Определить величину силы, которую нужно приложить ко всей системе, чтобы точка ее приложения стала ниже на 10 см.

Решение происходит по этапам:

1. Растяжение верхней и нижней пружин характеризуются формулой:

\(\triangle x2=F/k\)

2. Поскольку средние пружины подсоединены параллельно, их растяжение происходит в соответствии с формулой:

\(\triangle x2=F/2k\)

Каждая из пружин при этом растянется на: \(\triangle x1/2\)

Следовательно, справедливо математическое выражение: \(\triangle x2=\triangle x1/2\)

 Через промежуточные формулы:

\(2,5\triangle x1=\triangle x\)

\(\triangle x1=\triangle x/2,5\)

\(10/2,5=4\)

находим конечную формулу для решения задачи:

\(F=k\triangle x1=10\ast0,04=0,4\)

Ответ: сила равна 0,4 Н.

Задача 3

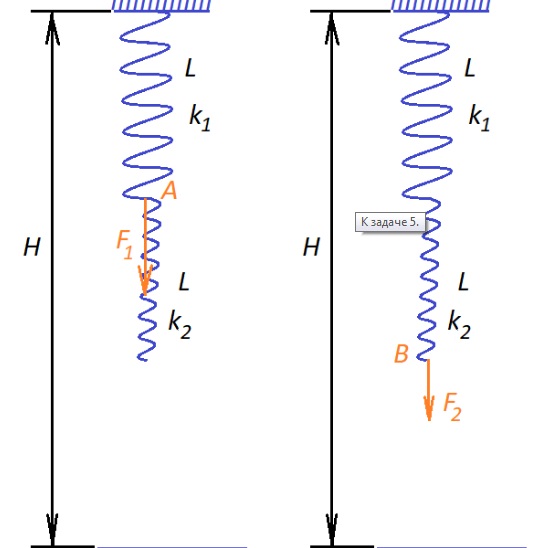
Один из тренажеров в спортивном зале высотой 2 м состоит из двух пружин, которые закреплены на потолке. Их длина одинакова (40 см), а жесткости обозначены k1, k2. При приложении к одной из пружин силы 360 Н (в точке А), нижняя ее часть пружина опустится до самого пола. Потянув в точке В и приложив силу 240 Н, коснется пола сама эта точка. Какова жесткость пружин?

Прикладывая усилия к точке А, вызываем растяжение только пружины сверху. Когда ее длина достигнет 1,6 м, нижняя коснется пола. Таким образом, верхняя удлинилась на 1,2 м.

\(L+\triangle l1=H-L\)

\(\triangle l1=H-2L=1,2\)

\(k1=F1/\triangle l1=360/1,2=300\)

Относительно точки В действуют формулы:

\(F2/k1+F2/k2=H-2L\)

\(240/300+240/k2=1,2\)

Значит \(k2=240/0.4=600\)

Ответ: коэффициенты пружин будут равны 300 и 600 Н/м.

Задача 4

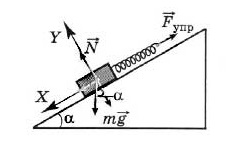
Пружина массой 5 кг прикреплена к бруску, который лежит неподвижно на поверхности. Как изменится сила ее натяжения, если угол наклона будет увеличиваться от 30^о до 60^о?

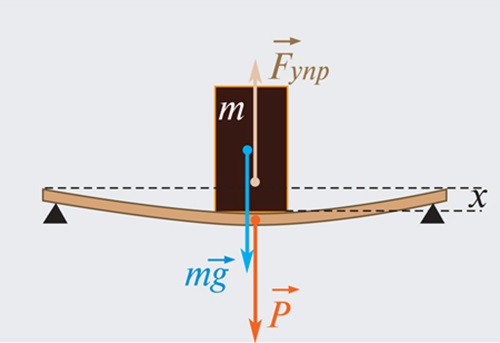
Как видно из рисунка, брусок испытывает влияние трех сил: тяжести, натяжения пружины, реакции опоры.

Для равновесия бруска необходимо равенство величин:\(mg=Fупр=N=0\)

Откладывая величины на осях координат, выходим на формулы:

\(mg\sin\alpha-\;\;Fупр=0\)

\(N\;-\;mg\;\cos\alpha\;=\;0\)

Из первого уравнения следует: 

\(Fупр=m\ast g\ast\sin\alpha\)

Учитывая, что угол наклона поверхности, на которой расположен брусок, меняется, ΔF_yпp можно определить по формуле:

\(\Delta Fyпp\;=\;mg(\sin\alpha2\;-\;\sin\alpha1)\;\)

Подставляя в формулу значения, высчитывают значение искомой силы:

ΔF_yпp=5 * 10 * (0,866 - 0,5) = 18,3 Н

Те, кому нужна практическая или теоретическая помощь в освоении темы по силе упругости, могут обратиться на Феникс.Хелп. Вам всегда помогут.