Спин и момент импульса: просто о сложном
Рассказываем, что такое спин с точки зрения физики и как он проявляется в бозонах и фермионах.
Что такое момент импульса?
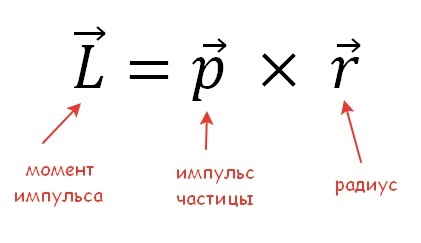
Теоретическая физика разделяет классическую и квантовую механику. Момент импульса в привычном определении ньютоновской механики — физическая величина, которая характеризует количество вращательного движения, а сама формула выглядит так:
Т.е. момент импульса может быть определен относительно точки в пространстве и оси объекта.
В квантовой механике, объясняющей взаимодействия и свойства частиц, такая величина тоже есть. Как и объекты макромира, частицы могут вращаться вокруг точки в пространстве и своей оси, а значит, иметь орбитальный момент импульса.
А что такое спин?
Спин — еще одна величина, которая объяснима только в рамках квантовой механики. Это собственный момент импульса, характеризующий внутреннее вращательное состояние частицы, не зависящее от внешних условий.
Увидеть и объяснить, что именно происходит внутри частицы, невозможно (по крайней мере, на данный момент). Ученые предположили существование спина на основании математических вычислений.
Спиновое квантовое число
Для того чтобы охарактеризовать собственный момент импульса частицы, теоретики ввели еще одно понятие — спиновое квантовое число J (иногда его тоже сокращенно называют «спин», но это не совсем точно). Его значение пропорционально приведенной постоянной Планка:
У каждой частицы свое спиновое число. Например, у бозонов (читали нашу статью о поисках бозона Хиггса?) — целый спин, а у фермионов — полуцелый.
Бозоны vs фермионы
Эти частицы — неотъемлемые составляющие Стандартной модели. К бозонам относятся фотон, глюон, бозон Хиггса. Они подчиняются статистике Бозе-Эйнштейна, допускающей, что в одном квантовом состоянии может находиться неограниченное количество одинаковых частиц.
Фермионы — электрон, лептон, кварк — подчиняются статистике Ферми-Дирака, т.е. в одном квантовом состоянии может находиться не более одной частицы.
Понять, что именно стоит за этими пространными определениями, можно, представив отличия бозонов и фермионов на примерах объектов из макромира.
Допустим, спин объекта А равен 0 — представим его в виде точки. При вращении А мы не увидим изменений.
Спин объекта B (пусть это будет карандаш, заточенный с одной стороны) равен 1. В таком случае В будет выглядеть с разных сторон по-разному. Нам придется повернуть его на 360˚, чтобы увидеть таким же, как в исходной точке.
Спин объекта C (одинаково заточенный с двух сторон карандаш) равен 2. Такой предмет достаточно повернуть на 180˚, чтобы получить такое же изображение, какое мы могли наблюдать в исходной точке.
Полуцелый спин ½ будет у объекта, который для повтора изображения нужно повернуть на 720˚. Например, точка, движущаяся по ленте Мёбиуса.
Надеемся, что мы помогли разобраться в том, что такое спин и какое значение он имеет в квантовой механике. А если этой информации оказалось недостаточно, не стесняйтесь обращаться за более подробной консультацией к специалистам Феникс.Хэлп.
Понравилась статья?
Подпишитесь на наш блог и получайте наши статьи первым!
Или подписывайтесь на нас в соцсетях:
Заметили ошибку? Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так

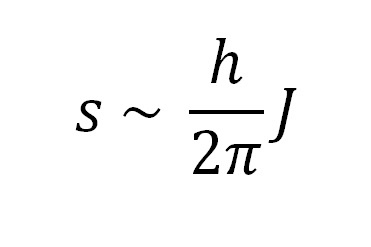

Бесплатно отвечаем на ваши вопросы. Задайте свой вопрос и получите ответ от профессионального преподавателя. Выберите лучший ответ.
Вопросы могут задавать только авторизованные пользователи. Войти