Производная функции: суть, решение с примерами
Производная функции – одно из фундаментальных понятий в математике, без понимания которого становится невозможным решение большинства математических и физических задач. Что же это такое?
Производная функции — краткое описание, суть
Если совсем просто, то:
Производная – это скорость изменения функции в данной точке.
Выражаясь математическим языком, это предел отношения приращения функции к приращению её аргумента при стремлении приращения аргумента к нулю. Формула:
Она понимается в двух смыслах: геометрическом и физическом.
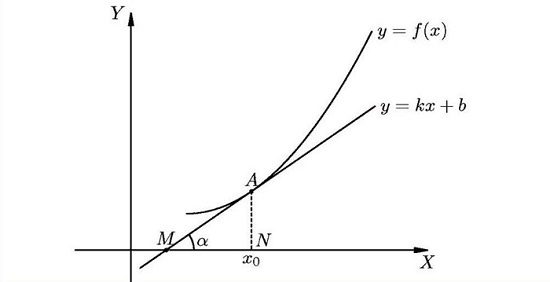
Геометрический смысл: производная от функции в точке равна тангенсу угла между осью OX и касательной к графику функции в данной точке.
Физический смысл: производная пути по времени равна скорости прямолинейного движения. Таким образом, значение скорости в определённый момент времени t0 определяется по формуле:
Вычисление производной называется дифференцированием. Обратный процесс – интегрированием.
Основные правила нахождения производных
Дифференцирование строится на следующих правилах.
Правило №1: производная от произведения числа на функцию равна
(c * f (x))' = c * f' (x),
где с – любое число.
Правило №2: производная от суммы функций равна
(f (x) + g (x))' = f ' (x) + g' (x).
Правило №3: производная от разности функций равна
(f (x) – g (x))' = f ' (x) – g' (x).
Правило №4: производная от произведения двух функций равна
(f (x) g (x))' = f ' (x) g (x) + f (x) g' (x).
Правило №5: производная от дроби равна
Существует и так называемая сложная функция (композиция функции) вида f (g(x)). В данном случае f (x) считается внешней функцией, g (x) – внутренней.
Правило дифференцирования сложной функции
Производная сложной функции вычисляется по формуле:
[ f (g (x))]' = f ' (g (x)) g' (x).
Пример нахождения
Задача: продифференцировать (x+2)¹⁰. Обозначим её как u=x+2.
Решение: так как (x¹⁰)'=10x⁹,
то ((x+2) ¹⁰)'=(u¹⁰)'=10u⁹⋅u'=10(x+2) ⁹⋅1=10(x+2) ⁹.
Ответ: 10(x+2) ⁹.
Логарифмическая производная
Логарифмическая производная — это производная от натурального логарифма функции.
Вычисляется по формуле:
Часто применяется для упрощения дифференцирования некоторых функций.
Пример поиска производной
Пусть y = y(x).
Для удобства прологарифмируем данную функцию:
ln y = ln y(x).
Теперь вычислим производную по правилу дифференцирования сложной функции:
Из этого следует, что
Тогда ответ:
Производная обратной функции
Теорема: для дифференцируемой функции с производной, не равной нулю, производная обратной функции равная обратной величине производной данной функции.
Общая формула:
Формулы и пример решения
Производные обратных тригонометрических функций:
Задача: продифференцировать y=x²-7lnx.
Решение: находим по формуле
отсюда
Производная функции, заданной параметрически
Пусть функция задана параметрическим уравнением:
Тогда производная равна:
Формулировка, решение примеров
Задача: продифференцировать функцию.
Решение: (при записи производной всегда необходимо писать t в нижнем индексе)
Подставляем в формулу:
Ответ:
В ответе составляется система, в которой кроме полученной производной необходимо писать х = t – 4.
Производная неявной функции
Если функция у = у(х) задана уравнением F (x; y(x)) = 0 то говорят, что она задана неявно.
Теоретическое обоснование
Для нахождения производной неявной функции нужно:
- Продифференцировать обе части уравнения по независимой переменной х предполагая, что у – это дифференцируемая по х функция.
- Решить полученное уравнение относительно производной у' (х).
Решение в примерах
Задача: решить функцию , заданную неявно:
Решение:
1) перенесём 3у -1 в левую часть и дифференцируем обе части равенства
Получим
Считая, что у – это функция от х, находим производную как от сложной функции:
Тогда
Для заданной функции имеем:
2) Решаем полученное уравнение относительно у':
Ответ:
Полная таблица производных
Приводим табличную форму, которая существенно облегчает вычисления:
Формул из этого списка достаточно для дифференцирования любой элементарной функции.
Решение элементарных производных, примеры
Задача№1: найти производную функции
Решение: данная функция является сложной, поэтому
Ответ:
Задача №2: найти производную функции
Решение:
Ответ:
Изучение производных и интегралов занимает большое количество времени. ФениксХэлп может помочь вам в решении контрольных и самостоятельных работ по этой теме и многим другим.
Понравилась статья?
Подпишитесь на наш блог и получайте наши статьи первым!
Или подписывайтесь на нас в соцсетях:
Заметили ошибку? Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так

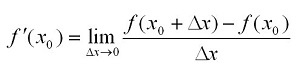
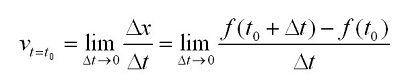
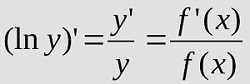
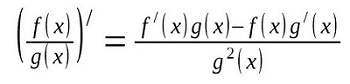
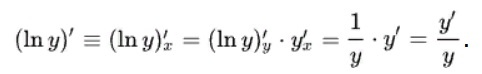
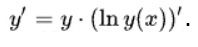
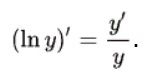
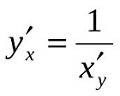
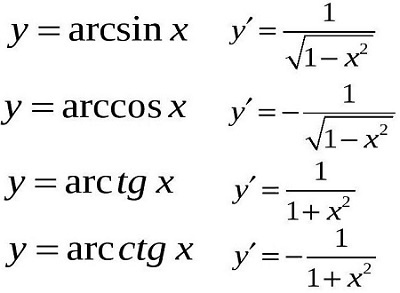
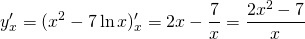
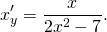
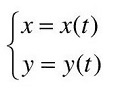

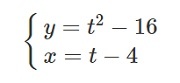
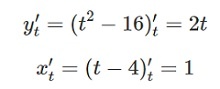
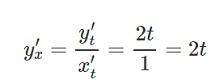
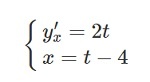
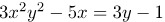
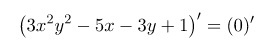
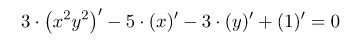
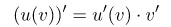
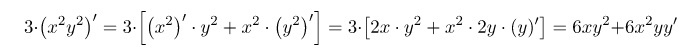
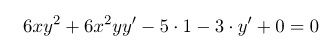
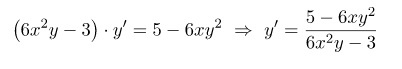
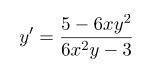
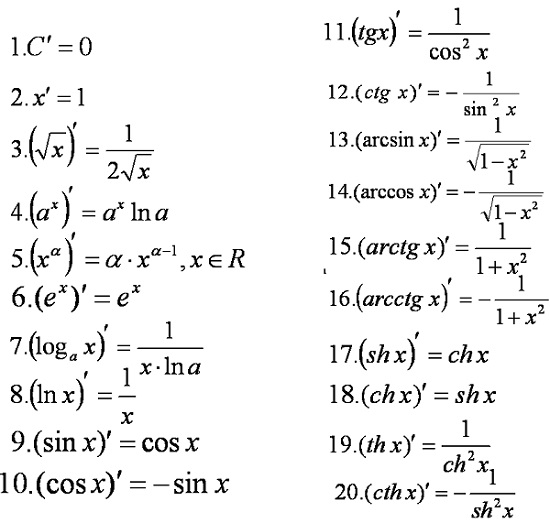
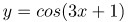
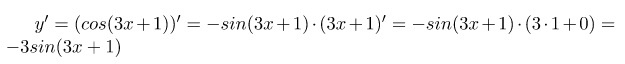
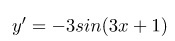

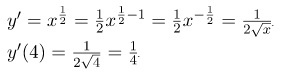
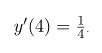
Бесплатно отвечаем на ваши вопросы. Задайте свой вопрос и получите ответ от профессионального преподавателя. Выберите лучший ответ.
Вопросы могут задавать только авторизованные пользователи. Войти