Решение дифференциальных уравнений
Уравнения встречаются повсеместно. С помощью формул и их систем рассчитывают разные величины и описывают физические процессы. С древних времен сферы применения уравнений только увеличиваются. К примеру, дифференциальные уравнения необходимы для освоения информатики, компьютерных технологий, физики.
Решение дифференциальных уравнений
Дифференциальные уравнения решают с помощью производных, которые являются пределами отношений приращения функций к приращению аргумента, при том, что приращение аргумента приближается к нулевому значению. Порядок таких уравнений соответствует наивысшему порядку производной, которая включена в уравнения. Степень определяется максимальной степенью, возведенной производной наивысшего порядка.
Решить дифференциальное уравнение — значит, найти множество всех функций, удовлетворяющих данному уравнению.
Такие множества записывают в следующем виде:
\(y = f(x;C)\)
где С представляет собой произвольную постоянную.
Общее решение дифференциального уравнения n-го порядка является некой функцией, которая зависит от аргумента x и n-го числа независимых произвольных постоянных.
Основные способы решения системы
При наличии навыков решения однородных уравнений второго порядка и неоднородных уравнений второго порядка, в состав которых включены постоянные коэффициенты, справиться с системами дифференциальных уравнений достаточно просто. Выделяют ключевые типы СДУ:
- линейные однородные;
- линейные неоднородные.
Решают системы дифференциальных уравнений несколькими методами:
- метод исключения, с помощью преобразования системы к одному дифференциальному уравнению;
- по средствам характеристического уравнения или способом Эйлера.
Линейные однородные системы дифференциальных уравнений
В качестве максимально простой однородной системы дифференциальных уравнений можно рассмотреть такую:
k, l, m, n являются числовыми коэффициентами, которые в большинстве случаев обладают ненулевыми значениями;
x(t), y(t) — функциональные значения, которые нужно найти;
t — самостоятельная переменная;
\(x',\;y'\) — первичные производные находимых значений вышеупомянутых функций.
В качестве примера можно решить систему дифференциальных уравнений, называемую задачей Коши:
Начальные условия будут следующими:
х (0) = 3
у (0) = 0
В данном случае целесообразно воспользоваться методом исключения. Способ состоит в том, чтобы преобразовать систему в одно дифференциальное уравнение.
В первую очередь следует функцию \(\ y(t)\) выразить с помощью функции \(\ x(t)\) и ее производной:
\( \ \frac{d x}{d t}=x^{\prime}(t)=-2 x+4 y \Rightarrow 4 y=x^{\prime}+2 x \Rightarrow y=\frac{x^{\prime}+2 x}{4}=\frac{x^{\prime}}{4}+\frac{x}{2}\)
Далее нужно определить производную функции \(\ y(t)\):
\(\ y^{\prime}=\left(\frac{x^{\prime}}{4}+\frac{x}{2}\right)^{\prime}=\frac{x^{\prime \prime}}{4}+\frac{x^{\prime}}{2}\)
Выполним преобразования путем подстановки выражений функции \(\ y(t)\) и ее производной во второе уравнение заданной системы. Получим следующее уравнение:
\(\ \frac{x^{\prime \prime}}{4}+\frac{x^{\prime}}{2}=-x+3 \cdot\left(\frac{x^{\prime}}{4}+\frac{x}{2}\right)\)
Если раскрыть скобки и свести подобные, то получим:
\(\ \frac{x^{\prime \prime}}{4}+\frac{x^{\prime}}{2}=-x+\frac{3 x^{\prime}}{4}+\frac{3 x}{2} \Rightarrow \frac{x^{\prime \prime}}{4}-\frac{x^{\prime}}{4}-\frac{x}{2}=0\)
Затем следует умножить обе части на 4:
\(\ \frac{x^{\prime \prime}}{4}+\frac{x^{\prime}}{2}=-x+\frac{3 x^{\prime}}{4}+\frac{3 x}{2} \Rightarrow \frac{x^{\prime \prime}}{4}-\frac{x^{\prime}}{4}-\frac{x}{2}=0\)
Таким образом, получилось однородное дифференциальное уравнение второго порядка относительно неизвестной функции:
\(\ x^{\prime \prime}-x^{\prime}-2 x=0 \)
Требуется найти его решение. Можно записать соответствующее характеристическое уравнение такого вида
\(\ x(t)\), корни которого \(\ k^{2}-k-2=0\)
В таком случае:
\(\ k_{1}=-1, \ k_{2}=2\)
Найти вторую неизвестную функцию:
\(\ x(t)=C_{1} e^{k_{1} t}+C_{2} e^{k_{2} t}=C_{1} e^{-t}+C_{2} e^{2 t} \)
Можно с помощью полученного выражения:
\(\ y(t): \ y=\frac{x^{\prime}}{4}+\frac{x}{2}\)
Таким образом, искомым решением системы является:
\(\ y(t)=\frac{1}{4}\left(C_{1} e^{-t}+C_{2} e^{2 t}\right)^{\prime}+\frac{1}{2}\left(C_{1} e^{-t}+C_{2} e^{2 t}\right)==\frac{1}{4}\left(-C_{1} e^{-t}+2 C_{2} e^{2 t}\right)+\frac{1}{2}\left(C_{1} e^{-t}+C_{2} e^{2 t}\right) =-\frac{C_{1} e^{-t}}{4}+\frac{C_{2} e^{2 t}}{2}+\frac{C_{1} e^{-t}}{2}+\frac{C_{2} e^{2 t}}{2}=\frac{C_{1} e^{-t}}{4}+C_{2} e^{2 t}\)
Для поиска частного решения рассматриваемой системы нужно подставить соответствующие значения в систему и определить константы:
Получим частное решение системы в виде:
Линейные неоднородные системы
Данный тип уравнений, как правило, имеет вид:
где \(f(t)\), \(g(t)\) — заданные функции переменной \(t\), непрерывные на \(\left[a,b\right]\).
В качестве примера можно рассмотреть решение следующей системы дифференциальных уравнений:
Используем значения из первого уравнения системы:
\(y=\frac15(-\frac{\operatorname dx}{\operatorname dt}+2x+3)\\\)
Дифференцируем по t все составляющие:
\(\frac{\operatorname dy}{\operatorname dt}=\frac15\left(-\frac{\mathrm d^2x}{\mathrm dt^2}+2\frac{\operatorname dx}{\operatorname dt}\right)\\\)
Подставим \(y=\frac15\left(-\frac{\operatorname dx}{\operatorname dt}+2x+3\right)\\\) и \(\frac{\operatorname dy}{\operatorname dt}=\frac15\left(-\frac{\mathrm d^2x}{\mathrm dt^2}+2\frac{\operatorname dx}{\operatorname dt}\right)\\\).
Получим:
\(\frac15\left(-\frac{\mathrm d^2x}{\mathrm dt^2}+2\frac{\operatorname dx}{\operatorname dt}\right)=5x-6\cdot\frac15\left(-\frac{\operatorname dx}{\operatorname dt}+2x+3\right)+1\\\)
Чтобы сократить дроби, нужно все части уравнения умножить на 5:
\(-\frac{\mathrm d^2x}{\mathrm dt^2}+2\frac{\operatorname dx}{\operatorname dt}=25x-6\cdot\left(-\frac{\operatorname dx}{\operatorname dt}+2x+3\right)+5\\\)
Далее упростим выражение:
\(-\frac{\mathrm d^2x}{\mathrm dt^2}+2\frac{\operatorname dx}{\operatorname dt}=25x+6\frac{\operatorname dx}{\operatorname dt}-12x-18+5\\\frac{\mathrm d^2x}{\mathrm dt^2}+4\frac{\operatorname dx}{\operatorname dt}+13x=13\\\)
В результате получилось линейное неоднородное уравнение второго порядка с постоянными коэффициентами. Следует найти общее решение уравнения:
\(\frac{\mathrm d^2x}{\mathrm dt^2}+4\frac{\operatorname dx}{\operatorname dt}+13x=0\\\)
Необходимо разобрать характеристическое уравнение:
\(\lambda^2+4\lambda+13=0\\D=16-52=-36\\\lambda_{1,2}=\frac{-4\pm6i}2\\\lambda_{1,2}=-2\pm3i \)
Таким образом, найдены сопряженные комплексные корни. В результате:
\(X=e^{-2t}\left(C_1\cos\left(3t\right)+C_2\sin\left(3t\right)\right)\)
Неоднородное уравнение:
\(\widetilde x=A\)
Рассчитываем значение первой и второй производных:
\(\widetilde x'=0\\\widetilde x''=0\)
Подставляем \(\widetilde x,\;\widetilde x',\widetilde x''\) в левую часть неоднородного уравнения:
\(0+4\cdot0+13A=13\\13A=13\\A=1\\\)
Получаем:
\(\widetilde x=1\)
Таким образом:
\(x(t)=X+\widetilde x=e^{-2t}\left(C_1\cos\left(3t\right)+C_2\sin\left(3t\right)\right)+1\)
Необходимо найти функцию \(y(t)\). Для этого нужно определить производную от уже найденной функции \(x(t)\):
\(x'(t)=\left(e^{-2t}\left(C_1\cos\left(3t\right)+C_2\sin\left(3t\right)+1\right)\right)'=\left(e^{-2t}\right)'\left(C_1\cos\left(3t\right)+C_2\sin\left(3t\right)\right)+e^{-2t}\left(C_1\cos\left(3t\right)+C_2\sin\left(3t\right)\right)'+0=\\=-2e^{-2t}\left(C_1\cos\left(3t\right)+C_2\sin\left(3t\right)\right)+e^{-2t}\left(-3C_1\sin\left(3t\right)+3C_2\cos\left(3t\right)\right)=e^{-2t}\left(-2C_1\cos\left(3t\right)-2C_2\sin\left(3t\right)-3C_1\sin\left(3t\right)+3C_2\cos\left(3t\right)\right)=\\=e^{-2t}\left(\left(-2C_1+3C_2\right)\cos\left(3t\right)+\left(-3C_1-2C_2\right)\sin\left(3t\right)\right)\)
Подставим \(x(t)=e^{-2t}\left(C_1\cos\left(3t\right)+C_2\sin\left(3t\right)\right)+1\) и \(x'(t)=e^{-2t}\left(\left(-2C_1+3C_2\right)\cos\left(3t\right)+\left(-3C_1-2C_2\right)\sin\left(3t\right)\right)\) в уравнение \(y=\frac15\left(-\frac{\operatorname dx}{\operatorname dt}+2x+3\right)\)
Получим:
\(y=\frac15\left(-e^{-2t}\left(\left(-2C_1+3C_2\right)\cos\left(3t\right)+\left(-3C_1-2C_2\right)\sin\left(3t\right)\right)+2\left(e^{-2t}\left(C_1\cos\left(3t\right)+C_2\sin\left(3t\right)\right)+1\right)+3\right)=\\=\frac15\left(e^{-2t}\left(\left(2C_1-3C_2\right)\cos\left(3t\right)+\left(3C_1+2C_2\right)\sin\left(3t\right)\right)+e^{-2t}\left(2C_1\cos\left(3t\right)+2C_2\sin\left(3t\right)\right)+2+3\right)=\\=\frac15\left(e^{-2t}\left(\left(2C_1-3C_2\right)\cos\left(3t\right)+\left(3C_1+2C_2\right)\sin\left(3t\right)+2C_1\cos\left(3t\right)+2C_2\sin\left(3t\right)\right)+5\right)=\\=\frac15\left(e^{-2t}\left(\left(2C_1-3C_2+2C_1\right)\cos\left(3t\right)+\left(3C_1+2C_2+2C_2\right)\sin\left(3t\right)\right)+5\right)=\\=e^{-2t}\left(\left(\frac{4C_1-3C_2}5\right)\cos\left(3t\right)+\left(\frac{3C_1+4C_2}5\right)\sin\left(3t\right)\right)+1\)
Общее решение системы будет иметь вид:
Приступаем к поиску частного решения, исходя из условий задачи:
Можно записать окончательный ответ:
Метод характеристического уравнения (метод Эйлера)
Данный способ применяется крайне редко. Целесообразно рассмотреть алгоритм метода Эйлера или характеристического уравнения на конкретном примере. Пусть дана линейная однородная система дифференциальных уравнений:
Следует записать матрицу, которая будет включать коэффициенты при неизвестных функциях в правых частях уравнений системы:
\(\ A=\left(\begin{array}{ll}{-1} & {-5} \\ {-7} & {-3}\end{array}\right)\)
Далее необходимо рассчитать собственные значения записанной матрицы с помощью характеристического уравнения и его корней:
\(\ |A-\lambda E|=0 \Rightarrow\left|\left(\begin{array}{cc}{-1} & {-5} \\ {-7} & {-3}\end{array}\right)-\lambda \cdot\left(\begin{array}{cc}{1} & {0} \\ {0} & {1}\end{array}\right)\right|\)
\(\left|\begin{array}{cc}{-1-\lambda} & {-5} \\ {-7} & {-3-\lambda}\end{array}\right|\)
\((-1-\lambda)(-3-\lambda)-(-7) \cdot(-5)\)
\(\lambda^{2}+4 \lambda-32=0\)
\({\lambda_{1}=-8}\)
\({\lambda_{2}=4}\)
Далее нужно определить собственные векторы, соответствующие полученным собственным значениям.
Если \(\ \lambda_{1}=-8\), то в этом случае определить координаты собственного вектора можно с помощью системы, кторая эквивалентна уравнению
\(\ 7 x_{1}-5 x_{2}=0 \Rightarrow x_{1}=\frac{5 x_{2}}{7} \)
При \(\ x_{2}=7\) получаем, что \(\ x_{1}=5\). Тогда первый собственный вектор \(\ \overline{x}_{1}=(5 ; 7).\)
\(\ \lambda_{2}=4\)
\(\Rightarrow\left(A-\lambda_{2} E\right) \overline{x}_{2}=\overline{0}\)
\(\Rightarrow x_{1}+x_{2}=0, \Rightarrow x_{1}=-x_{2}\)
Для \(\ x_{2}=1\) получаем второй собственный вектор \(\ \overline{x}_{2}=(-1 ; 1).\)
Тогда общее решение исконной системы дифференциальных уравнений
\(C_{1} e^{\lambda_{1} t} \overline{x}_{1}+C_{2} e^{\lambda_{2} t} \overline{x}_{2}\)
\(C_{1} \cdot e^{-8 t} \cdot\left(\begin{array}{c}{5} \\ {7}\end{array}\right)+C_{2} \cdot e^{4 t} \cdot\left(\begin{array}{c}{-1} \\ {1}\end{array}\right)\)
\(\left(\begin{array}{c}{5 C_{1} e^{-8 t}} \\ {7 C_{1} e^{-8 t}}\end{array}\right)+\left(\begin{array}{c}{-C_{2} e^{4 t}} \\ {C_{2} e^{4 t}}\end{array}\right)\)
\(\left(\begin{array}{c}{5 C_{1} e^{-8 t}-C_{2} e^{4 t}} \\ {7 C_{1} e^{-8 t}+C_{2} e^{4 t}}\end{array}\right) \)
Можно записать окончательный ответ:
С системами дифференциальных уравнений работать гораздо проще, если освоить основные приемы решений. В том случае, когда по данной теме или любой другой возникают какие-либо сложности, всегда можно обратиться за помощью к сервису Феникс.Хелп.
Понравилась статья?
Подпишитесь на наш блог и получайте наши статьи первым!
Или подписывайтесь на нас в соцсетях:
Заметили ошибку? Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так

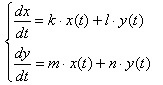
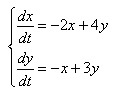

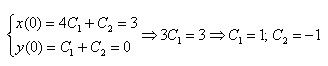
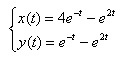
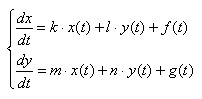
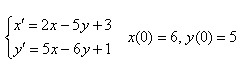

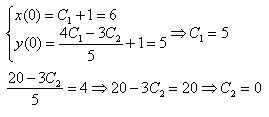
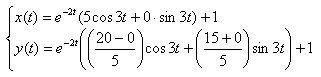
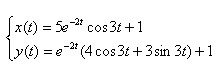
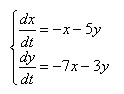
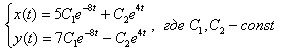

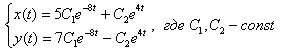

Бесплатно отвечаем на ваши вопросы. Задайте свой вопрос и получите ответ от профессионального преподавателя. Выберите лучший ответ.
Вопросы могут задавать только авторизованные пользователи. Войти