Качественные задачи по теме "Электростатика"

Разбираемся с физическим понятием электростатики и учимся применять формулы в решении задач.

Электростатика — что это за раздел физики

Электростатика — это раздел электродинамики, который изучает электрически заряженные тела, находящиеся в покое, и их взаимодействие друг с другом.

Вы уже знакомы со многими электростатическими явлениями, хотя и не подозреваете об этом. Например, притяжение воздушного шарика к шерстяному свитеру или смешная прическа после зимней шапки — это и есть явления электростатики.

Они возникают вследствие взаимодействия электрических зарядов. Сила, образованная подобным взаимодействием, определена законом Кулона. Звучит он так:

Сила взаимодействия двух точечных зарядов в вакууме направлена вдоль прямой, соединяющей эти заряды, пропорциональна их величинам и обратно пропорциональна квадрату расстояния между ними. Она является силой притяжения, если знаки зарядов разные, и силой отталкивания, если эти знаки одинаковы.

Выраженный в формуле, закон Кулона выглядит следующим образом:

\(F=k\cdot\frac{q_1\cdot q_2}{r^2}\)

где \(q_1\) и \(q_2\) — точечные заряды, \(r\) — расстояние между зарядами, \(k\) — коэффициент пропорциональности, который в системе СИ: \(k=\frac1{4\pi\varepsilon_0}=9\cdot10^{-18}\frac{Н\cdot м^2}{Кл^2}. \) 

\(\varepsilon_0 \)— электрическая постоянная, \(\varepsilon_0=8,85\cdot10^{-12}\) \(\frac{Ф}{м}\).

В векторной форме закон Кулона выглядит так:

\(\overrightarrow F=k\cdot\frac{q_1\cdot q_2}{r^2}\cdot\overrightarrow{e_r}\)

где \(\overrightarrow{e_r}\) — единичный вектор, направленный от заряда \(q_1\) к \(q_2.\)

Сначала может показаться, что эти силы довольно слабы. Но на самом деле, такое взаимодействие, как у протона и электрона в атоме водорода, на 36 порядков больше, чем гравитация между ними же. Эффект от этих электростатических сил тоже может оказаться колоссальным и непредсказуемым. Например, электризация зерна в зернохранилищах может привести к спонтанному возгоранию и печальным последствиям.

Качественные задачи по электростатике

Без решения задач и применения теории на практике нам не обойтись. Поэтому разберемся с примерами решения задач на электростатику.

Задача 1

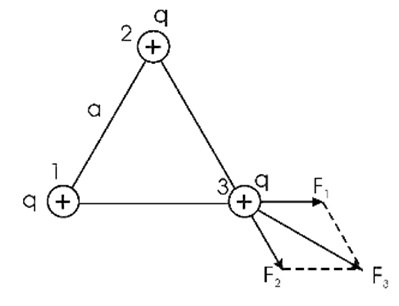
Даны три одинаковых равных заряда \(q_1=q_2=q_3=2\)нКл. Они находятся на вершинах равностороннего треугольника со сторонами a=10см. Нужно определить модуль и направление силы F, которая действует на один из зарядов со стороны двух других.

Решение:

Для наглядности, нарисуем:

Для решения этой задачи нужно применить закон Кулона. Сила, с которой взаимодействуют заряды 1 и 2 равна. Формула выглядит так:

\(F_1=\frac1{4\pi\varepsilon\varepsilon_0}\cdot\frac{\left|q_1\right|\cdot\left|q_2\right|}{a^2}\)

Известно, что заряды равны. Поэтому:

\(F_1=F_2=\frac1{4\pi\varepsilon\varepsilon_0}\cdot\frac{q^2}{a^2}.\)

Так как наш треугольник равносторонний, все его углы равны \(60^\circ\). Сила, которую мы ищем, направлена по биссектрисе угла. Используем формулу:

\(F=F_3=2F_1\cdot\cos\left(30\right)=\frac1{2\pi\varepsilon\varepsilon_0}\cdot\frac{q^2}{a^2}\cdot\cos\left(30\right)\)

Подставим сюда известные значения и получаем:

\(F=2\cdot9\cdot10^9\cdot\frac{4\cdot10^{-18}}{0,01}\cdot\cos\left(30\right)=6,2\) мкН

Ответ: 6,2 мкН.

Задача 2

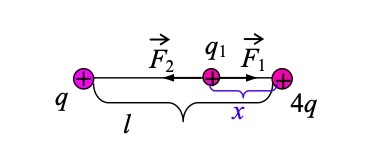
Даны два положительных точечных заряда \(q\) и \(4q\), которые закреплены на расстоянии l=60 см друг от друга. Нужно вычислить, в какой точке на прямой между двумя этими зарядами нужно поместить третий \(q_1\) так, чтобы он находился в равновесии. Также нужно определить, какой должен быть знак у данного заряда, чтобы равновесие было устойчивым, при условии, что перемещения заряда доступны только вдоль прямой, проходящей через два закрепленных заряда.

Решение:

Поместим заряд \(q_1\) на некотором расстоянии от заряда \(4q\) и расставим силы Кулона \(F_1\) и \(F_2\), которые действуют на него. Чтобы заряды были в равновесии, нужно, чтобы сила \(F_1\), которая действует от \(q\) на \(q_1\), была равна силе \(F_2\), которая действует от \(4q\) на \(q_1\).

Распишем все в виде формул:

\(F_1=F_2\)

\(\frac1{4\pi\varepsilon_0}\cdot\frac{q\cdot q_1}{{(l-x)}^2}=\frac1{4\pi\varepsilon_0}\cdot\frac{4q\cdot q_1}{x^2}\)

\(\frac1{{(l-x)}^2}=\frac4{x^2}\)

\(x^2-4l^2+8lx-4x^2=0\)

\(-3x^2+8lx-4l^2=0\)

\(D=64l^2-4\cdot3\cdot4l^2=16l^2\)

\(x_1=\frac{-8l-4l}{-6}=2l,\;x_2=\frac{-8l+4l}{-6}=\frac23l\), а так как мы понимаем, что \(x\) не может быть больше \(l\), то \(x=\frac23l=\frac23\cdot60=40\) см.

Ответ: 1) 40 см.

2) Так, для устойчивого состояния равновесия \(q_1\) должен быть положительным. Если он сместится ближе к \(4q\), то будет сильнее отталкиваться от него, а со стороны заряда \(q\) сила отталкивания станет меньше. Это значит, что \(q_1\) вернется на свое место.

Задача 3

Определить силу, с которой будут притягиваться два одинаковых свинцовых шарика радиусом r=1см, которые расположены на расстоянии R=1м, если у каждого атома первого шарика отнять по одному электрону и все отнятые электроны перенести на второй шарик. Известно, что молярная масса свинца \(М=207\cdot10^{-3}\)кг/моль, а плотность \(\rho=11,3г/см^3\).

Решение:

Так как электроны отняты у одного шарика и перенесены на другой, шарики приобретают равные и противоположные по знаку заряды. Если они находятся в вакууме, то сила притяжения выражается:

\(F=\frac{q^2}{4\pi\varepsilon_0R^2}\)

Где \(R\) — расстояние межу центрами шариков.

Заряд \(q\) же определяется как:

\(q=e\cdot\frac mM\cdot N_A=e\cdot\frac{\rho V}M\cdot N_A=\frac4{3M}\varepsilon\rho\pi r^3N_A\)

где \(N_A=6,02\cdot10^{23}моль^{-1}\) — число Авогадро

Таким образом:

\(F=\frac1{4\pi\varepsilon_0}\cdot\frac{{\displaystyle\frac4{3M}}e\rho\pi r^3N_A}{R^2}=\frac49\cdot\frac{\pi{N^2}_Ar^6\rho^2e^2}{\varepsilon_0M^2R^2}=4,38\cdot10^{18}H\)

Ответ: \(4,38\cdot10^{18}H\)

Если все равно ничего не понятно, а контрольная уже на носу, пиши специалистам из ФениксХелп. Они помогут с задачами любой сложности.