Как решать типовые задачи по физике

Обучаясь в школе, каждый сталкивается с решением задач по физике. Не всем дисциплина дается легко.

Бытует мнение, что для успешного решения задач по этому предмету, нужно досконально разбираться в физических процессах. Это не совсем так. Мы считаем, что достаточно использовать определенный алгоритм, чтобы добиться значительных успехов. Спешим поделиться с вами ценной информацией!

Как решать задачи по физике

Итак, чтобы задачи по физике давались легко, предлагаем придерживаться следующей системы:

1. Внимательно прочитайте условия задачи, при необходимости, несколько раз; вникнете в то, о чем говорится в тексте.
2. Запишите условия. Все известные в задаче данные нужно записать в столбик под названием «Дано». Обратите внимание, во многих задачах по физике, данными для решения являются и названия вещества. Например, дана задача: «Сколько понадобится железнодорожных цистерн для перевозки 1000 тонн нефти, если вместимость каждой цистерны 50 \(м^3\)?». Известными данными в ней будут: масса (m), равная 1000 тонн, объем цистерны (V), равный 50 \(м^3\) и плотность (p) нефти, по таблице плотностей равная 800 \(кг/м^3\). Также не забывайте про постоянные величины, например, ускорение свободного падения. В задачах на свободное падение о нем может быть не сказано ни слова, но оно предполагается в условиях и необходимо, чтобы их решить. Подумайте об этом, когда записываете все известные данные.
3. С столбце «СИ» приведите все данные в задаче к международным единицам измерения. Так как в международной системе основными единицами измерения массы считаются килограммы (кг), массу из приведенной выше задачи необходимо привести в нужное значение: 1 000 тонн = 1 000 000 кг. 
4. Нарисуйте схематичный рисунок. Он нужен не для всех задач. Но в тех, где упоминаются действующие на тело силы и векторы скоростей, изображение может существенно облегчить понимание процесса и натолкнуть на правильное решение.
5. Определите неизвестную величину, ту, что необходимо узнать, решив задание. Написав в столбике все, что известно в задаче, проведите черту под известными данными и пропишите ту величину, которую будете искать.
6. Подберите формулы. Это самый важный пункт в нашем алгоритме! Решение задачи после выбора формулы будет заключаться в математических вычислениях, которые имеют к физике лишь опосредованное отношение. На черновике выпишите те формулы, которые могут подойти для конкретной задачи и выберите ту, которая будет способствовать решению.
7. Математические вычисления. Остальное решение задачи сводится к математике. Нужно сделать необходимые преобразования и сокращения, если они нужны. Затем составить уравнение или систему уравнений. Остается только их решить и найти все неизвестные, а в конце искомую величину. Ответ обведите в прямоугольник. 

Примеры решения типовых задач по разделам

Рассмотрим подробнее решение задач из разных разделов физики по предложенному алгоритму. И дадим все необходимые объяснения к каждой из них.

Кинематика

Кинематика — это раздел механики, который изучает математическое описание движения тел. 

Данный раздел охватывает следующие темы:

• равномерное и равноускоренное движение тел;
• движение тела по окружности;
• относительность движения;
• свободное падение тел.

Рассмотрим типовые задачи на каждую из этих тем.

Равномерное и равноускоренное движение тел

Для решения задач по этой теме нужно знать уравнение движения тела, понимать, что такое средняя, постоянная скорости и ускорение, уметь выяснять их векторное направление в конкретной задаче.

Как правило, в задачах на равномерное и равноускоренное движение необходимо найти или пройденный путь (S), или скорость движения (V), или время (t).

Задача:

Поезд длиной 240 метров, двигаясь равномерно, прошел мост за 2 минуты. Какова была скорость поезда, если длина моста равна 360 метрам?

Решение:

1. Записываем известные нам данные:\( l_1=240\) м., \(l_2=360\) м., \(t=2\) мин., \(V\)=?
2. Проводим необходимые преобразования времени до принятых в мире единиц измерения — секунд: 2 минуты = 120 секунд.
3. Мы знаем, что скорость равномерного движения определяется по формуле: \(V=\frac st\) 
4. Время нам известно, для того, чтобы найти скорость, нужно сначала определить путь пройденный поездом. Если мы схематично изобразим перемещение поезда по мосту, то увидим, что путь, пройденный поездом, равен длине самого поезда плюс длине самого моста, т.е. \(s=l_1+l_2\).
5. Переходим к математическим вычислениям: \(s=240+360=600\) метров.
6. \(V=600/120= 5\) м/с.

Задача:

При равноускоренном движении с начальной скоростью 5 м/с тело за 3 секунды прошло 20 метров. С каким ускорением двигалось тело? Какова его скорость в конце третьей секунды?

Решение:

1. Фиксируем данные известных нам величин: \(V_1=5 \) м/с, \(t=3\) с, s=20 м., \(a=?\) ,\(V_2=?\) В условиях все величины даны в международных единицах, ничего переводить не нужно. 
2. Мы знаем формулу нахождения пути при равноускоренном движении: \(S=V_1\times t+\frac{at^2}2\) 
3. Из нее выводим уравнение для вычисления ускорения: \(a=\frac{2x\left(s-v_1\times t\right)}{t^2}\)
4. Подставляем известные данные и получаем ускорение, равное приблизительно \(1,1 м/с^2.\)
5. Нам известна формула для определения скорости при равноускоренном движении: \(V_2=V_1+a\times t\)
6. Все данные у нас для вычисления скорости есть, подставляем их в формулу и получаем скорость, равную \(8,3\) м/с.

Движение тела по окружности

Чтобы успешно решать задачи по этой теме, необходимо знать формулы, характеризующие движение тел по окружности. В задачах на движение тела по окружности обычно необходимо вычислить скорость, центростремительное ускорение, радиус или длину окружности.

Задача:

Каково центростремительное ускорение поезда, который движется по закругленной железной дороге радиусом 800 метров со скоростью 72 км/ч?

Решение:

1. Записываем вводные данные: \(R=800 м\), \(V=72\) км/ч, \(a\)=?
2. Переводим скорость из км/ч в м/с, получаем 20 м/с.
3. Мы знаем формулу, по которой можно определить центростремительное ускорение: \(a=\frac{V^2}R\)
4. Все данные нам известны, подставляем числовые значения в формулу и получаем искомую нами величину, равную \(0,5 м/с^2\)

Свободное падение тел

Для решения задач по этой теме нужно знать закон движения при свободном падении и закономерность изменения скорости тела со временем, а также помнить про постоянную величину — коэффициент силы тяжести.

В задачах на свободное падение тел может быть предложено найти скорость движения тела, высоту, с которой оно падало или время его движения.

Задача:

Камень брошен вниз с высоты \(85\) метров. Он летит со скоростью \(8\) м/с. С какой скоростью он ударяется о землю?

Решение:

1. Определяем известные и неизвестные нам данные: \(h=85\) метров, \(V_1=8\) м/с., \(V_2=?\) Мы помним, что на любое падающее тело воздействует коэффициент силы тяжести, равный \(9,8\) Н/кг.
2. У нас есть все вводные для определения конечной скорости по формуле: \(V_2=V_1+g\times t\)
3. Подставляем числовые значения в уравнение и получаем скорость тела в момент удара о землю, равную \(41,3\) м/с.

Относительность движения

Задачи на относительность движения всегда требует выбрать неподвижную систему координат, относительно которой и будут производиться все расчеты. В таких заданиях ученикам обычно предлагают найти относительную скорость объекта, минимальное время, продолжительность пути или длину объекта.

Задача:

Два поезда движутся навстречу друг другу по параллельным ж/д путям. Один — со скоростью 72 км/ч, другой — со скоростью 54 км/ч. Пассажир первого поезда отмечает, что второй проходит мимо него в течение 10 секунд. Определите длину второго поезда.

Решение:

1. Записываем известные нам данные: \(V_1=72\) км/ч, \(V_2=54\) км/ч, \(t=10\) с, \(l_2=?\)
2. Переводим км/ч в м/с: \(V_1= 20\) м/с, \(V_2=15\) м/с.
3. Определяем систему координат, от которой будем отталкиваться при вычислении искомой величины. Логично будет, если такой системой станет линейная система координат, связанная с первым поездом и направленная по ходу его движения. Получается, что второй поезд двигается со скоростью \(V_2=15\) м/с в направлении со скоростью \(V_1=20\) м/с.
4. Находим общую скорость движения по формуле: \(V=V_1+V_2\) 
5. Она равна \(35\) м/с.
6. Определяем длину поезда по формуле: \(l_2=V\times t\)
7. Получаем длину поезда, равную \(350\) метрам.

Динамика

Динамика — это раздел физической дисциплины, который изучает взаимодействие тел друг другом, причины изменения движения тел и силы, воздействующие на тело в тот или иной момент времени.

Этот раздел механики охватывает следующие темы:

• законы Ньютона; 
• неподвижный блок и наклонная поверхность; 
• закон всемирного тяготения;
• сила упругости, упругий и неупругий удар; 
• работа, энергия, мощность;
• закон сохранения энергии и импульса.

Для выполнения заданий по динамике необходимо знать законы Исаака Ньютона, силы, воздействующие на тела, закон сохранения импульса и уметь рисовать несложные рисунки, иллюстрирующие движение и взаимодействие тел.

Законы Ньютона

Задача: 

Велосипедист катится с горы с ускорением, равным \(0,8 м/с^2\), масса велосипедиста вместе с велосипедом составляет \(50\) кг. Определите силу, под воздействием которой велосипедист осуществляет движение.

Решение:

1. Записываем известные и неизвестные вводные: \(a=0,8 м/с^2\), \(m=50\) кг, \(F=?\)
2. По второму закону Ньютона: \(F=m\times a\)
3. Подставляем числовые значения в формулу и получаем, значение силы, действующей на велосипедиста, равное \(40\) Н.

Неподвижный блок и наклонная поверхность

Закон всемирного тяготения

Задача:

Две книги массой 600 грамм каждая лежат на расстоянии 1 метра друг от друга. Определите силу, с которой оба предмета притягиваются друг другу?

Решение:

1. Записываем известные данные: m_1=600 г, \(m_2=600\) г, \(r=1\) м, \(F=?\) Не забываем про гравитационную постоянную \(G\), которая равна \(6,67х10^-11 Нхм^2/кг^2\)
2. Переводим граммы в килограммы. Каждая книга получается по \(0,6\) кг.
3. По формуле закона всемирного тяготения: \(F=G\times\frac{m_1\times m_2}{r^2}\) вычисляем силу притяжения между книгами.
4. Произведя математические вычисления получаем ответ: книги притягиваются друг к другу с силой приблизительно равной \(2,4\) Н.

Сила упругости

Задача: 

К покоящейся на горизонтальной поверхности системе, которая состоит из куба массой 1 кг и 2-х пружин, приложена постоянная горизонтальная сила величиной 25 Ньютонов. Между кубом и поверхностью трения нет. Жесткость первой пружины составляет  \(450 Н/м\), жесткость второй пружины \(550 Н/м\). Определите удлинение пружин.

Решение:

1. Записываем в столбце «Дано» данные, которые нам известны: \(m=1\) кг,\( F=25\) Н, \(k_1=450\) Н/м, \(k_2=550\) Н/м, \(\Delta l_1=?\), \(\Delta l_2=? \) 
2. Согласно 3-му закону Ньютона \(F=F_упр\)
3. По закону Гука \(F_упр=F=k\times\Delta l\) отсюда выводим формулы для нахождения удлинения пружин: \(\Delta l_1=\frac F{k_1}\) и \(\Delta l_2=\frac F{k_2}\)
4. Подставляем известные нам числовые значения в формулы и получаем ответ: \(6 см\) — удлинение первой пружины, \(5 см\) — удлинение второй пружины.

Работа, энергия, мощность

Задача:

С плотины с высоты 20 м каждую минуту падает \(18000 м^3\) воды. Какая при этом выполняется работа.

Решение:

1. Запишем известные нам условия: \(h= 20 м\), \(V=18000 м^3\), \(t=1\) мин, \(A=?\) Также из условий задачи мы знаем вещество — воду, а значит по таблице плотности веществ, находим значение плотности воды: \( p=1000 кг/м^3\). А так как вода падает с высоты вертикально вниз, в процессе участвует ускорение свободного падения \(g=9,8 м/с^2.\)
2. Переводим минуты в часы: \(1\) минута=\(60\) секунд.
3. Найти работу можно по формуле: \(A=F\times S\)
4. В данных условиях \(S=h\), а \(F=g\times m\)
5. В условиях задачи нет значения массы тела, но мы помним, что массу можно найти по формуле: \(m=p\times V\)
6. Формула нахождения работы приобретает следующий вид: \(A=p\times V\times g\times h\)
7. Подставляем известные числовые значения в формулу и получаем ответ: работа = 3 528 000 000 Дж = 3 528 МДж. 

Закон сохранения энергии и импульса

Задача:

Тепловоз массой 130 тонн приближается со скоростью 2 м/с к неподвижному составу массой 1170 тонн. С какой скоростью будет двигаться состав после сцепления с тепловозом? 

Решение:

1. Записываем известные нам данные: \(m_1=130\) тонн, \(V_1=2\) м/с, \(m_2=1170\) тонн,  \(V_2=0\) м/с, V=?
2. Согласно закону сохранения импульса \(m_1\times V_1+m_2\times V_2=m_3\times V_3\)
3. Из этой формулы получаем уравнение для нахождения скорости состава после сцепления: \(V_3=\frac{m_1\times V_1}{m_1+m_2}\)
4. Подставляем известные нам значения в формулу и получаем искомую скорость, равную \(0,2\) м/с.

Статика

Статика — третий раздел механики, который изучает механические системы в условиях равновесия и действие приложенных к ним сил.

Для решения задач по статике необходимо обязательно рисовать схемы, иллюстрирующие заданные процессы, определять модули и направления сил, пользоваться законами сопротивления материалов.

Статика включает в себя следующие разделы:

• равновесие тел;
• давление в жидкостях и газе;
• закон Архимеда.

Равновесие тел

Давление в жидкостях и газе

Задача:

Водолаз в жестком скафандре может погружаться на глубину 250 метров, искусный ныряльщик — на 20 метров. Определите давление воды в море на этих глубинах.

Решение:

1. Записываем известные нам данные из условия задачи: \(h_1\)=250 м, \(h_2\) =20 м, \(p=1030 кг/м^3\), \(g=9,8\) Н/кг, \(p_1=?,\) \(p_2=?\)
2. По формуле \(P_1=p\times g\times h_1\) определяем давление воды для водолаза, оно будет равно примерно 2524 кПа.
3. По формуле \(P_2=p\times g\times h_2\) определяем давление воды для ныряльщика, получаем величину, равную 202 кПа.

Закон Архимеда

Задача:

Сила Архимеда, которая действует на полностью погруженное в керосин тело, равна 1,6 Н. Найдите объём этого тела.

Решение:

1. Фиксируем вводные: \(F_а=1,6\) Н, \(p=800 кг/м^3\), \(g=9,8\) Н/кг, \(V=?\)
2. Из формулы: \(F_а=p\times g\times V\) выводим формулу для вычисления объема: \(V=\frac F{p\times g}\)
3. Подставляем числовые значения в формулу и считаем объем, получается примерно \(0,0002 м^3.\)

Молекулярная физика

Молекулярная физика — это один из разделов физики, описывающий физические свойства объектов путем изучения их молекулярного строения.

В основе всех задач по молекулярной физике лежит уравнение молекулярно-кинетической теории: \(P=\frac13\times m_0\times n\times V_2\)

Термодинамика

Термодинамика — физический раздел, который изучает общие свойства макроскопических систем, способы передачи и превращения энергии в них.

В раздел термодинамики входят следующие темы:

• теплота сгорания топлива; 
• изменение внутренней энергии тела при совершении работы; 
• внутренняя энергия идеального газа;
• первый закон термодинамики;
• КПД теплового двигателя.

Теплота сгорания топлива

При решении задач на сгорание топлива, важно помнить про удельную теплоту сгорания каждого вида топлива.

Задача:

Чему будет равно количество теплоты, которое выделится при полном сгорании пороха массой 25 грамм?

Решение:

1. Записываем исходные данные: \(m=25\) г, удельная теплота сгорания пороха \(q=0,38\times10^7\) Дж/кг, \(Q=?\)
2. По формуле \(Q=q\times m\) определяем теплоту сгорания и получаем 95 кДж.

Изменение внутренней энергии тела при совершении работы

Задача:

Вычислите внутреннюю энергию 1 килограмма воды при ее нагревании на 2 Кельвина.

Решение:

1. Записываем известные и неизвестные величины из условий задачи: \(m=1\)  кг, \(T=2\)К, \(U=?\), не забываем про удельную теплоемкость воды \(c=4200\) Дж/кгхК.
2. Количество теплоты, которое получит вода, будет затрачено на изменение ее внутренней энергии, т.е. \(U=Q\).
3. \(Q=c\times m\times T\) следовательно, \(U=c\times m\times T\)
4. Подставляем числовые значения в формулу и получаем ответ: 8400 Дж.

Внутренняя энергия идеального газа, первый закон термодинамики

При решении таких задач важно помнить про молярную массу вещества и универсальную газовую постоянную.

Задача:

Чему будет равна внутренняя энергия гелия массой 200 грамм при условии, что температура будет увеличена на 20 Кельвинов? 

Решение:

1. Фиксируем известные величины: \(m=200\) г, \(\Delta T= 20\) К., молярная масса гелия \(M=0,004\) кг/моль, мольная теплоемкость для одноатомного газа \(R=8,31\) Дж х моль/К,  \(\Delta Q=?\)
2. Согласно первому закону термодинамики, рассчитываем изменение внутренней энергии по следующей формуле: \(\Delta Q=\frac{3m}{2M}\times R\times \Delta T\)
3. Путем математических вычислений получаем ответ: 12,5 кДж.

КПД теплового двигателя

Задача:

Определите КПД нагревающего устройства, которое расходует 80 грамм керосина при нагревании 3 литров воды на 90 Кельвинов.

Решение:

1. Зафиксируем известные нам данные: \(m_2=80\) г, \(V_1=3\) л, \(T=90\) К, \(\eta=?\) Из условий задачи мы также знаем удельную теплоемкость воды \(c_1=4200\) Дж/кгхК, плотность воды \(p_1=1000 кг/м^3\), удельную теплоту сгорания керосина \(q=43\) МДж/кг.
2. Приводим данные величины к международным единицам измерения: массу — в килограммы, объем — в \(м^3\).
3. Коэффициент полезного действия определяется по формуле: \(\eta=\frac{A_п}{A_з}\)
4. \(A_п\) равна количеству теплоты (\(Q\)), которое необходимо для изменения температуры воды. \(A_п=Q=c\times m\times T.\) Массу воды найдем по формуле: \(m_1=p_1\times V_1\)
5. \(A_з\) равна количеству теплоты, выделенному при сгорании керосина массой 80 грамм, следовательно, \(A_з=q\times m_2\)
6. Подставив все известные величины в формулу, получаем ответ: КПД = 0,33.

Электростатика

Электростатика — это раздел физики об электричестве, который изучает взаимодействие электрических зарядов, находящихся в неподвижности.

К задачам по электростатике относятся задачи на :

• закон Кулона; 
• напряженность и работу электростатического поля; 
• электроемкость.

Закон Кулона

Задача:

Определите силу взаимодействия двух одинаковых точечных зарядов по 1 микро кулону, которые находятся на расстоянии 30 сантиметров друг от друга. 

Решение:

1. Запишем исходные данные: \(Q_1=1\) мкКл, \(Q_2=1\) мкКл, \(r=30\) см, \(F=?\) Не забываем про коэффициент пропорциональности \(k=9х10^9 Нхм^2/Кл^2\).
2. Переведем микро кулоны в кулоны, сантиметры — в метры.
3. Силу находим по формуле: \(F=\frac{q_1\times q_2}{r^2}\)
4. Подставляем числовые значения в формулу и получаем ответ: 0,1 Н.

Напряженность электростатического поля

Задача:

На заряд \( 2,7х10^-6\) Кл в некоторой точке электрического поля действует сила 0,015 Ньютонов. Определите напряженность поля в этой точке.

Решение:

1. Записываем условия: \(q=2,7х10^-6\) Кл, \(F=0,015\) Н, \(E=?\)
2. Формула для определения напряженности электрического поля: \(E=\frac Fq\)
3. Подставляем числовые значения в формулу и определяем напряженность: 6000 Н/Кл.

Электроемкость

Задача:

При напряжении 220 вольт заряд на конденсаторе составляет 30 мкКл. Какова электроемкость этого конденсатора?

Решение:

1. Записываем «Дано»: \(U=220\) В, \(q=30\) мкКл, C=?
2. Приводим единицы измерения к международным стандартам — кулонам: \(3\times10^{-6}\) Кл.
3. По формуле \(C=\frac qU\) определяем электроемкость и получаем величину, равную \(13,6\) мкФ.

Электродинамика

Электродинамика включает в себя два больших раздела:

1. Постоянный и переменный ток.
2. Магнитное поле.

Постоянный и переменный ток

К задачам на постоянный и переменный ток относятся задачи на:

• закон Ома для участка цепи; 
• закон Ома для полной цепи; 
• работа и мощность тока.

Задача на закон Ома:

По медному проводнику длиной 40 метров и площадью сечения 2 \(мм^2\) протекает ток 5 Ампер. Чему равно напряжение на концах этого проводника?

Решение:

1. Записываем известные и искомую величины:\( l=40м\), \(S=2 мм^2\), \(I=5A\), \(U=?\) Из условий мы также можем знать плотность меди \(p=0,017 Ом\) \( мм^2/м\).
2. Согласно закону Ома \(I=\frac UR\) отсюда \(U=U=I\times R\)
3. Сопротивление определяем по формуле: \(R=p\times\frac lS\)
4. Подставляем числовые данные, находим сопротивление. Оно равно 0,34 Ом.
5. Находим значение напряжения: 1,7 В.

Задача на работу и мощность тока:

Определите мощность и работу электродвигателя вентилятора за 10 минут, если при напряжении 220 Вольт сила тока в электродвигателе составила 1 Ампер.

Решение:

1. Записываем условия: \(t=10\) мин, \(U= 220\) В, \(I=1 А\), \(P=?\) \(A=?\)
2. Переводим минуты в секунды, получаем 600 секунд.
3. По формуле \(P=I\times U\) определяем мощность тока. Она равна 220 Вт.
4. По формуле \(A=P\times t\) находим работу, получаем 132000 Дж или 132 кДж.

Магнитное поле

К задачам раздела «Магнитное поле» относятся задания на:

• силу Ампера;
• силу Лоренца; 
• магнитный момент, индукцию и самоиндукцию, энергию магнитного поля.

Задача на силу Ампера:

Прямолинейный проводник имеет массу 2 килограмма и длину 0,5 метра. Его поместили в однородное магнитное поле, которое перпендикулярно линиям индукции 15 Тесла. Какой силы должен быть ток, проходящий по нему, чтобы этот проводник висел, а не падал?

Решение:

1. Записываем вводные: \(m=2\) кг, \(l=0,5\) м, \(B=15\) Тл, \(\alpha= 90\) градусов, \(g=10 м/с^2\), \(I=?\)
2. Формула для определения силы ампера: \(F=I\times B\times l\times\sin\alpha\) отсюда \(I=\frac F{B\times l\times\sin\alpha}\)
3. Находим \(F\) по формуле: \(F=m\times g\)
4. Соответственно, силу тока можно найти по формуле: \(I=\frac{m\times g}{B\times l\times\sin\alpha}\)
5. Производим математические вычисления и получаем ответ: 2,67 А.

Задача на силу Лоренца:

Чему равна сила Лоренца, которая действует на электрон, движущийся в магнитном поле по окружности радиусом 0,03 метров, если скорость электрона \(10х10^6 м/с\), а масса электрона \(9х10^-31\) килограмм?

Решение:

1. Записываем данные: \(r=0,03\) м, \(V=10х10^6 м/с\), \(m=9х10^-31\) кг, \(F_л=?\)
2. Сила Лоренца определяется по формуле: \(F_л=m\times a_ц\)
3. В свою очередь, \(a=\frac{V^2}R\)
4. Все данные известны, подставляем численные значения в формулу и получаем силу Лоренца, равную \(3х10^-15 Н\).

Задача на магнитный поток и ЭДС индукции:

Колебания и волны

В разделе физики «Колебания и волны» изучают следующие темы:

• механические гармонические колебания математических маятников;
• пружинный маятник; 
• энергия механических колебаний; 
• механические волны; 
• колебательный контур;
• электромагнитные волны.

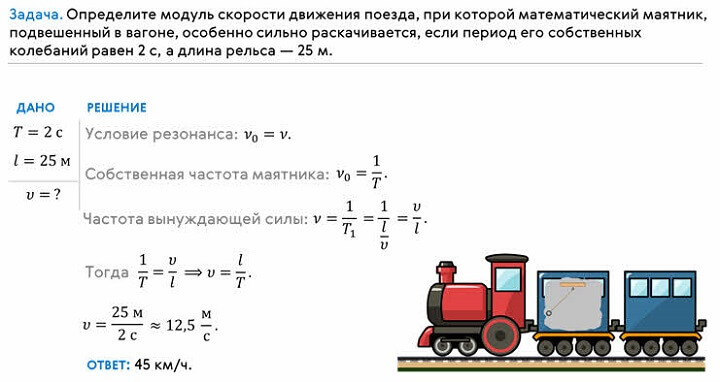
Задача на колебания математического маятника:

Задача на пружинный маятник:

Задача на колебательный контур:

Для того, чтобы задания по физике решались совсем легко, предмет нужно полюбить. Если это не про вас, не переживайте! Посвящайте свое время любимым дисциплинам и хобби, а физику оставьте для профессионалов Феникс.Хелп.