Задачи по физике на тему «механика» с решением

Все движущиеся тела подчиняются законам механики. Не составляет исключение параллельное взаимодействие с другими телами, а также изменение их положения во времени и пространстве. 

Что такое механика, какие области охватывает

Существует теоретическая сторона, которая затрагивает общие закономерности движения, включая планеты солнечной системы, а также характеристики полета, и дисциплины, изучающие частные моменты работы двигателей, механизмов, машин и их внутренних частей.

Исходя из этого, сформулировать предмет механики можно следующим образом:

• теоретическая сторона;
• механика сплошных сред;
• специальные разделы, такие как: механизмы и машины, гидравлические процессы, механика почв и т.п.

Почему возникла необходимость дифференциации на разделы? В ее основе лежат свойства времени, материи и нахождения в пространстве. Опираясь на такие характеристики, механика подразделяется на виды:

• классическую;
• релятивистскую;
• квантовую.

Изучая механические системы с учетом их степеней свобод, проводится обобщение импульсов и, при необходимости, наложение их на систему координат. Сама механическая система может являться замкнутой (изолированной от окружающих факторов) и незамкнутой (открытой). Вторая классификация оценивает характеристику во времени: статические и динамические. К динамическим системам, к примеру, относят математический, физический и крутильный маятники, твердое тело, неголономную систему, сплошную среду и др.

Общий курс школьной программы включает такие разделы, как механика, динамика, статика, кинематика. Решаются задачи в этих ключах, а также на законы сохранения.

Примеры решения задач по теоретической механике

Задача 1. Путь автомобиля ($S$) условно разделен на три части: первую, вторую и третью. Какой будет средняя скорость его движения на первой части ($V_1$), если средняя скорость ($V$) равна 37,5 км/ч, а скорость на второй и третьей частях пути ($V_2$) была равна 50 км/ч?

Решение:

Обозначим время, затраченное на первой трети пути $t_1$, на оставшихся двух третях — $t_2$.Тогда:

$t_1+t_2=S\div3V_1+2S\div3V_2$

$t_1+t_2=S\div V$

$V_1=VV_2\div(3V_2-2V)=$25 км/ч

Задача 2. Моторная лодка за 3 часа переплывает по реке из точки А в точку Б. На возвращение она тратит 5 часов. Зная, что скорость движения лодки одинаково туда и обратно, определите, сколько времени займет движение из точки А в точку Б у плота.

Если скорость теплохода $V_1$, а течения — $V_2$, то время, затраченное на весь путь от А до Б, составляет:

$t_1=S\div(V_1+V_2)$.

Путь от Б до А лодка прошла за:

$t_2=S\div(V_1-V_2).$

Выразим $S$ через $t$ и $V$, приравняв математические выражения пути через эти категории:

 $t_1(V_1+V_2)=t_2(V_1-V_2)$. 

Применив стандартные действия сложения, получаем: 

$V_1=4V_2$

В итоге отмечаем, что лодка без учета скорости течения пройдет путь за 4 часа. Ее скорость, когда она плывет против течения, в 3 раза превышает скорость реки.

Ответ: плот сможет преодолеть расстояние от А до Б за 15 часов.

Задача 3. Мужчина едет в поезде со скоростью 80 км/ч. Навстречу идет товарный поезд со скоростью 40 км/ч. Длина встречного состава — 1 км. На протяжение какого времени мужчина будет наблюдать из окна за движущимся встречным поездом?

Решение задачи можно провести двумя методами.

Метод 1. Если относительно Земли мужчина находился в точке с координатой $Х=О$, то окончание товарного поезда было от него удалено на 1 км ($Х_т=1$км). Координата первой точки $Х$ находится на расстоянии, определяемом по формуле $V_1t$, второй — $Х_т-V_2t$.

Когда хвост встречного поезда был на уровне мужчины-пассажира, $Х_1=Х_2$ или $V_1t=X_тt–V_2t$.

Отсюда $t=X_T\div(V_1+V_2)$

Метод 2. Если рассматривать положение мужчины относительно товарного поезда, его скорость будет равна $V_0=V_1+V_2$. Учитывая, что длина поезда 1000 м, мимо мужчины будут следовать его вагоны в течение времени:

$t=l\div(V_1+V_2)$

Подставив значение, получаем, что $t=20$ сек.

Задача 4. Тело подвесили на полуметровой нити. Она невесома и нерастяжима. Требуется определить минимальную скорость в горизонтальном направлении, которую надо сообщить телу, чтобы оно совершило полный оборот по вертикальной плоскости.

Алгоритм решения следующий. Согласно закону сохранения энергии для тела, переходящего из нижнего положения в верхнее, характерно:

$M{V_0}^2\div2=mg+2L+MV^2\div2$  ($L$ — длина нити). 

Когда тело находится вверху, на него воздействуют силы тяжести и натяжения нити. Они суммарно передают ему центростремительное ускорение, которое направлено вниз — в направлении точки подвеса: 

$Mа_ц=Mg+T$

По условию задачи тело должно достичь верхней точки, следовательно, $Т=0$. Поэтому:

$MV^2\div l=Mg$, откуда $V^2=gl$.

Подставляем выражения друг в друга и получаем:

$M{V_0}^2\div2=2Mgl+Mgl\div2$

${V_0}²=g4l+gl=5gl$

$V_0=\surd(5\ast10\ast0,5)$=5 (м/с)

Примечание. При условии расположения тела на жестком стержне, вверху скорость тела будет равна 0. При этом
$M {V_0}^2\div2=Mg2l$, отсюда

${V_0}^2=4gl$

$V_0=\surd(4gl)=2\surd(gl)$

Подставив значения, получаем ответ задачи.

$V_0=2\ast\surd(10\ast0,5)$=4,47(м/с)

Задача 5. При катании на роликах два человека взялись за разные концы одной веревки. При движении один из них получает ускорение. Каково ускорение второго катающегося, если он весит в 1,5 раза меньше? Силу трения между землей и поверхностью роликов в расчет не брать.

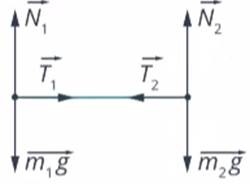
По материалам задачи понятно, что на катающихся действуют три силы:

• сила тяжести, измеряемая формулами m₁g и m₂g;
• реакция опоры N₁ и N_2;
• натяжение веревки между ними: T₁ и T₂.

Кроме того, катающиеся перекладывают друг на друга собственные силы, которые согласно третьему закону Ньютона равны по значениям, т.е. T₁=T₂=T. Направления этих сил указаны на рисунке.

Катающиеся получают ускорение, охарактеризовать которое можно по второму закону Ньютона. Поскольку между ними отсутствует жесткое соединение, эти значения могут отличаться.

Примечание. В объяснении к задаче следует учесть, что силу, с которой катающийся тянет веревку, не учитываем, поскольку задача направлена на анализ обратно направленной силы.

Решение:

По второму закону Ньютона, для каждого тела характерно:

m₁g+N₁+T₁=m₁a

m₂g+N₂+T₂=m₂a

Проведя проекции на ось Y, получается:

m₁g-N₁=0

m₂g-N₂=0

При проекции на ось Х:

T₁=m₁a₁

 -T₂=-m₂a₂ 

Если T₁=T₂=T, m₁=1,5m₂ (по условию задачи), то

T=1,5m₂a₁

T=m₂a₂

Проводя математические действия, выводим конечную формулу: a₂=1,5a₁

Ответ задачи: ускорение одного из катающихся в 1,5 раз больше, чем другого.

Задача 6. Обосновать расчетами, отличается ли сила тяжести, направленная на 2 литра воды от нее же, направленной на 2 литра ртути.

Формула силы тяжести: F=mg

Найти массу по формуле: $m=\rho V$,

где ρ-плотность вещества, а V — его объем.

Выводим итоговую формулу и, зная плотность и объем обоих веществ, подставляем значения:

$F_1=\rho_1{V_1}g$

$F_2=\rho_2V_2 g$

Тогда $F_1\div F_2=\rho_1V_1 g\div\rho_2 V_2 g$

Отсюда $F_1\div F_2=\rho_1V_1 \div\rho_2 V_2$

Находим табличные данные: ρ₁=1000 кг/м³; ρ₂=13540 кг/м³

Таким образом $F_1\div F_2$=0,07

Задача 7. Нужно определить показания механического динамометра, когда к нему будет подвешена гиря массой 0,8 кг. Каков в таком случае ее вес?

Поэтому: P=F=mg

Считая g=10 м/c², проводим вычисления:

P=F=0,8*10=8 Н

Задача 8. Зная, что возле поверхности Земли $g=9,81$м/с², необходимо определить величину ускорения на высоте $3R_z$.

Формула ускорения свободного падения, с учетом Закона всемирного тяготения, выглядит так:

$g=GM\div R^2$

$R$ — расстояние от тела до центра Земли.

Зная, что $R=R_z$, корректируем формулу:

$g=GM\div Rz^2$

G=6,67*10¹¹H*м² кг-2

Поскольку R=3R_z

$g=G\ast M\div Rz^2$

$g_2=G\ast M\div(3Rz)^2$

$g_2\div g=GM\div(3Rz)^2\div (GM\div R_z^2)=1/9$

$g_2=g\div9=1,09$ м/c²

Быстро и грамотно решить задачи на тему «Механика» помогут на сайте Феникс.Хелп. Обращайтесь, если катастрофически не хватает времени или вы не уверены в правильности собственных рассуждений. За решениями задержки не будет — здесь знают свое дело!