Правила решения интегралов для студентов
Интеграл является одним из наиболее важных понятий в математическом анализе. Его применяют в алгебре для расчета площади под кривой, преодоленного пути в процессе неравномерного движения, массы, которой обладает неоднородное тело и решения других подобных задач. С помощью интеграла вычисляют функцию по известной производной.
Интегралы для чайников — базовые понятия
Понятие интеграла в теории основано на нахождении непрерывной функции. Для начала следует ознакомиться с этим термином.
Непрерывная функция F(х) представляет собой первообразную функции f(х) на понятном промежутке х при условии, что F(х)=f(х).
Процедура поиска первообразной функции f(х) представляет собой операцию интегрирования в определенном порядке.
Интеграл в кратком смысле является аналогом суммы для бесконечного числа бесконечно малых слагаемых.
Неопределенный интеграл
Неопределенным интегралом называют комплекс всех первообразных функции f(х).
В легком виде формулу для расчета неопределенного интеграла можно записать в такой форме:
\(\int f(x)dx=F(x)+C\), где
- f(x) является подынтегральной функцией;
- F(x) представляет собой первообразную функцию функции f(x);
- dx определяется дифференциалом;
- C является численной константой интегрирования.
В неопределенный интеграл включен спектр первообразных, так как имеется постоянная интегрирования. Дифференциалом называют произвольное, бесконечно малое приращение переменной величины. Среди основных свойств неопределенного интеграла можно отметить такие пояснения:
Табличная форма неопределенных интегралов в виде \(\int f(x)dx=F(x)+C\) имеет вид:
Определенный интеграл
Определенным интегралом называют приращение одной из первообразных функции f(х), соответствующих отрезку [a;b].
В общем виде определенный интеграл можно записать таким образом:
\(\int_{a}^{b}{} f(x)dx\), где
- f(x) представляет собой подынтегральную функцию;
- a и b являются пределами интегрирования;
- dx соответствует дифференциалу.
Вычислить определенный интеграл можно с помощью уравнения Ньютона-Лейбница:
Свойства определенных интегралов:
- если определенный интеграл обладает одинаковыми пределами интегрирования, то его значение соответствует нулю;
- значение определенного интеграла является независимой от обозначения переменной интегрирования величиной;
- постоянный множитель допустимо выносить за знак определенного интеграла;
- определенный интеграл в случае алгебраической суммы конечного числа функций рассчитывается как алгебраическая сумма определенных интегралов;
- при разбивке отрезка интегрирования на части определенный интеграл в отношении всего отрезка соответствует сумме определенных интегралов его частей;
- перестановка пределов интегрирования не меняет абсолютную величину определенного интеграла, а изменяет его знак;
- определенный интеграл рассчитывается как произведение длины отрезка интегрирования и значения подынтегральной функции в какой-то точке х0 внутри него;
- в том случае, если верхний предел интегрирования больше, чем нижний, и подынтегральная функция соответствует неотрицательному или положительному значению, определенному интегралу будет соответствовать неотрицательная или положительная величина;
- когда верхний предел интегрирования больше, чем нижний, и функции f(х) и g(х) не прерываются, то допустимо почленно интегрировать неравенство f(x) >=g(x).
Таблица интегралов для студентов (основные формулы)
Существует несколько основных приемов решения задач с интегралами. Процесс заключается в интегрировании функции по переменной. В том случае, если интеграл обладает табличным видом, то проблем с поиском его значения не возникнет. Когда форма записи интеграла отлична от табличной, решение сводится к приведению интеграла к табличному виду.
Таблица первообразных для решения интегралов имеет следующий вид:
В первую очередь необходимо ознакомиться с основными свойствами интегралов:
С помощью данных понятий можно решать несложные интегралы. Но в большинстве случаев встречаются задачи с непростыми интегралами, для работы с которыми требуется прибегнуть к дополнительным приемам.
Правила вычисления интегралов, примеры решения
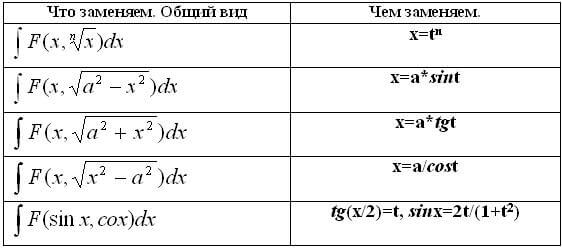
Специальные методики позволяют рассчитывать большую часть интегралов. Основными приемами для поиска решений являются:
- Замена переменной с применением навыков нахождения производных.
- Интегрирование по частям с помощью формулы: \(\int udv=uv-\int vdu\).
- Интегрирование дробно-рациональных функций:
- разложением дроби на простейшие \(\int F_{n}(x)/G_{m}(x)dx\);
- выделением полного квадрата \(\int dx/(ax^{2}+bx+c)\);
- созданием в числителе дифференциала знаменателя \(\int (mx+n)dx/(ax^{2}+bx+c)\).
- Интегрирование дробно-иррациональных функций:
- выделением под корнем полного квадрата \(\int dx/(\sqrt{ax^{2}+bx+c})\);
- созданием в числителе дифференциала подкоренного выражения \(\int (mx+n)dx/(\sqrt{ax^{2}+bx+c})\).
- Интегрирование тригонометрических функций:
- с помощью формул разложения для произведения \(\int \sin \alpha x*\cos \beta xdx\);
- с помощью создания \(d(cos x)\) при m-нечетном, n-любом для выражений вида \(\int \sin^{n}x*\cos^{m} xdx\) применимо тождество \(\sin^{2}+\cos^{2}=1\), где m, n являются четными, \(\sin^{2}x=(1-\cos^{2}x)/2$$ и $$ \cos^{2}x=(1+\cos^{2}x)/2\);
- Применение свойства \(\tan ^{2}x=1/\cos ^{2}x-1\) для выражения в виде \(\int tan^{n}xdx\).
Решать интегралы целесообразно с помощью данного алгоритма:
- Вникнуть в суть интегралов, включая базовые понятия и методы решения. Интеграл представляет собой сумму элементарных частей объекта интегрирования. В том случае, когда рассматривается интегрирование функции, следует идентифицировать интеграл как площадь фигуры между графиком функции, осью х и границами интегрирования. При неопределенном интеграле, то есть неизвестных границах интегрирования, решать задачу необходимо с помощью нахождения первообразной. В случае определенного интеграла в найденную функцию подставляют значения границ.
- Научиться пользоваться таблицей первообразных и основными свойствами интегралов. Множество функций уже определены первообразными, которые отмечены в таблице. Для интегралов, которые занесены в табличную форму, уже имеется готовое решение.
- Освоение способов и приобретение навыков решения интегралов. В том случае, когда в задаче имеется интеграл, не соответствующий табличной форме, его необходимо привести к этому виду. Данная операция выполняется с помощью применения основных свойств интегралов и приемов по их решению.
На первых этапах обучения следует проверять собственные решения задач на интегралы. Для этого можно дифференцировать полученное выражение и сравнить его с исходным интегралом.
Примеры решения интегралов:
Задача 1
Требуется решить интеграл:
\(\int (x^{5}+\frac{1}{\sqrt{x}})dx\)
Решение
Заметим, что по условию интеграл — неопределенный. Сначала необходимо найти первообразную. Для этого интеграл суммы можно разложить на сумму интегралов:
\(\int x^{5}dx+\frac{1}{\sqrt{x}}dx\)
Таким образом, каждый из интегралов преобразован в табличный вид. Решение можно найти с помощью таблицы:
\(\frac{x^{6}}{6}+2\sqrt{x}+С\)
Выполним проверку решения с помощью поиска производной:
\((\frac{x^{6}}{6}+2\sqrt{x})^{,}=x^{2}+\frac{1}{\sqrt{x}}\)
Ответ: \(\frac{x^{6}}{6}+2\sqrt{x}+С\)
Задача 2
Требуется решить интеграл:
\(\int \sqrt[5]{(x+5)}\)
Решение
Имеется неопределенный интеграл. Для начала необходимо найти первообразную. При сравнении с таблицей выяснилось, что подобное решение отсутствует. Способ разложения, исходя из свойств интеграла, не применим в данном случае. Следует обратиться к приемам. В этом случае целесообразно воспользоваться заменой переменной. Таким образом, выполним замену выражения \(х+5\) на \(t^{5}\).
\(t^{5}=x+5\)
После преобразований получим \(\int tdx.\)
Выражение dx также требуется заменить на t. В таком случае:
\(x=t^{5}-5\)
\(dx=(t^{5}-5)^{,}=5t^{4}\)
Выполним подстановку значений:
\(5\int t^{4}*tdt=5\int t^{5}dt\)
Интеграл соответствует табличной форме. Его можно посчитать \(\frac{5t^{6}}{6}\).
Далее необходимо заменить t на выражение \(\sqrt[5]{(x+5)}\).
Таким образом:
\(\int \sqrt[5]{(x+5)}=5/6\sqrt[5]{(x+5)^{6}}\)
Ответ: \(\int \sqrt[5]{(x+5)}=5/6\sqrt[5]{(x+5)^{6}}.\)
Задача 3
Необходимо найти решение интеграла:
\(\int \frac{dx}{\sqrt{4x^{2}+4x+5}}\)
Решение
В рамках данной задачи целесообразно выделить полный квадрат:
\(4x^{2}+4x+5=4x^{2}+4x+1+4=(2x+1)^{2}+1\)
\(\int \frac{dx}{\sqrt{4x^{2}+4x+5}}=\int \frac{dx}{\sqrt{(2x+1)^{2}+1}}=\frac{1}{2}\int \frac{d(2x+1}{\sqrt{(2x+1)^{2}+1}}\)
Результат преобразований соответствует табличному виду. Можно найти первообразную:
\(\int \frac{dx}{\sqrt{x^{2}+a^{2}}}=\ln \left|x+\sqrt{x^{2}+a^{2}} \right|+C\)
\(\int \frac{dx}{\sqrt{4x^{2}+4x+5}}=\ln \left|2x+1+\sqrt{(2x+2)^{2}+1} \right|+C\)
\((2x+1)^{2}+1=4x^{2}+4x+1\)
В результате получим:
\(\int \frac{dx}{\sqrt{4x^{2}+4x+5}}=\ln \left|2x+1+\sqrt{4x^{2}+4x+1} \right|+C\)
Ответ: \(\int \frac{dx}{\sqrt{4x^{2}+4x+5}}=\ln \left|2x+1+\sqrt{4x^{2}+4x+1} \right|+C\)
Математический анализ — достаточно сложная дисциплина. Одной из главных тем является решение интегралов. С подобными задачами часто сталкиваются учащиеся профильных вузов. Если в процессе обучения студент испытывает какие-либо трудности, правильное решение — обратиться к сервису Феникс.Хелп.
Понравилась статья?
Подпишитесь на наш блог и получайте наши статьи первым!
Или подписывайтесь на нас в соцсетях:
Заметили ошибку? Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так

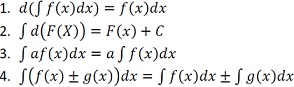



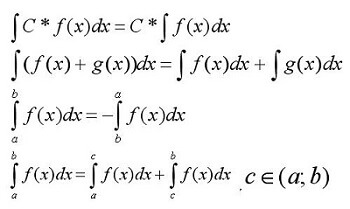


Бесплатно отвечаем на ваши вопросы. Задайте свой вопрос и получите ответ от профессионального преподавателя. Выберите лучший ответ.
Вопросы могут задавать только авторизованные пользователи. Войти