Решение задач с применением закона сохранения энергии

Многие явления, окружающие нас, объясняются с помощью законов физики. Одним из ключевых утверждений является закон сохранения энергии. Данный принцип взаимодействия разных типов энергии играют большую роль в развитии современной науки.

Что такое закон сохранения энергии

Закон сохранения энергии является универсальным утверждением. Для разных направлений науки физики оно может иметь неодинаковую формулировку, однако смысл тезиса остается неизменным. В рамках дисциплины классической механики рассматривают закон сохранения механической энергии.

В условиях замкнутой системы не наблюдается обмен энергией с окружающей средой. При этом ее собственная энергия сохраняет постоянство величины. Для такой системы характерны лишь внутренние силы и взаимодействие тел друг с другом. В системе потенциальная энергия превращается в кинетическую энергию и наоборот. Простейшим примером замкнутой системы является снайперская винтовка и пуля.

Разновидности сил в механике

Внутри механической системы действуют силы, которые могут быть консервативными и неконсервативными. К первому типу относят силы, для которых характерна работа, независящая от направления движения тела, на которое они воздействуют. Такие силы рассчитывают путем определения начального и конечного положения этого объекта. По-другому консервативные силы называют потенциальными. В условиях замкнутого контура их работа равна нулю. Примерами консервативной силы являются сила тяжести и сила упругости.

Остальные силы в системе относят к неконсервативным. Примерами таких сил являются сила трения и сила сопротивления. По-другому их называют диссипативными силами. Для них характерно отрицательное значение работы в условиях замкнутой механической системы при любых движениях объекта. При воздействии этих сил наблюдают убывание полной механической энергии системы. При этом энергия трансформируется в другие немеханические разновидности, к примеру, в тепло. Исходя из вышеизложенного, закон сохранения энергии в условиях замкнутой механической системы работает при отсутствии неконсервативных сил.

Полную механическую энергию системы можно представить как совокупность кинетической и потенциальной энергии, которые трансформируются друг в друга при определенных условиях.

Потенциальная энергия

Потенциальная энергия рассчитывается, исходя из взаимного расположения тел. На ее величину влияет расстояние между объектами. Расчет производится путем вычисления работы, которую необходимо совершить для транспортировки тела из точки отсчета в заданную точку в поле, для которого характерны консервативные силы.

Потенциальной энергией обладает любой физический объект, который находится в неподвижном положении на определенной высоте. В этом случае на тело воздействует сила тяжести, относящаяся к категории консервативных сил. Примерами тел, которые обладают такой энергией, являются вода на краю водопада или санки на вершине горы. Понять природу происхождения потенциальной энергии просто. В то время, когда объект поднимали до определенной высоты, была затрачена работа и энергия. Данная энергия осталась в запасе в поднятом теле и может быть использована для совершения работы.

Потенциальную энергию определяют высотой, на которой расположен объект, относительно начальной точки своего движения или другой точки, принятой за начало отсчета. В планетарном масштабе объекты, которые размещены на поверхности Земли, обладают нулевой потенциальной энергией. Но при подъеме на высоту \(h\), она увеличивается и становится равной:

\(E_П = mgh\)

где \(m\) обозначает массу объекта, \(g\) является ускорением свободного падения и равно 9,8 м/с², а \(h\) — это высота центра масс объекта относительно земной поверхности.

Если тело будет падать с высоты \(h_1\) до какой-то точки на высоте \(h_2\), можно наблюдать работу силы тяжести. Данная величина будет равна изменению потенциальной энергии и соответствует отрицательному значению. Это объясняется уменьшением потенциальной энергии при падении объекта.

\(A = - (E_{П2} – E_{П1}) = - Δ E_П\)

где \(E_{П1}\) является потенциальной энергией тела на высоте \(h_1\), а \(E_{П2}\) представляет собой потенциальную энергию объекта на \(h_2\).

В ситуации, когда объект поднимают на высоту, работа совершается против силы тяжести. Тогда ее величина будет положительной, а потенциальная энергия будет увеличиваться.

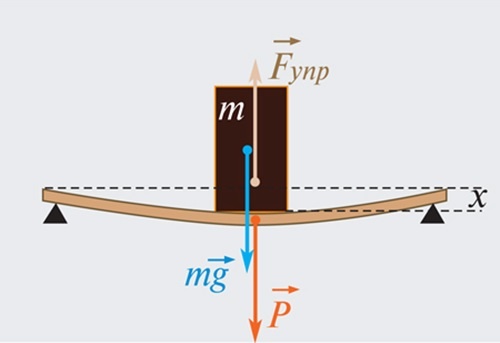
Наличие потенциальной энергии характерно и для упруго деформированного тела (к примеру, сжатой или растянутой пружины). Величина потенциальной энергии определяется жесткостью пружины и длиной ее сжатия или растяжения. Формула для расчета имеет следующий вид:

\(Е_П = k*(Δx)2/2\)

где \(k\) является коэффициентом жесткости, \(Δх\) — удлинением или сжатием объекта.

Потенциальная энергия пружины может совершать работу.

Кинетическая энергия

Величина кинетической энергии определяется скоростью движения объекта. Примерами тел, которые обладают кинетической энергией, являются:

• футбольный мяч, катящийся по полю;
• скатывающиеся с горы санки;
• стрела, выпущенная из лука, и др.

Покоящееся тело обладает нулевой кинетической энергией. При воздействии силы или нескольких сил оно приводится в движении. Во время перемещения объекта действующие на него силы совершают определенную работу. Данная величина изменяет скорость тела от нуля до значения \(V\) и называется кинетической энергией тела, масса которого равна \(m\). В случае, когда в начале временного отсчета объект уже двигался со скоростью \(V_1\), а в конечный момент приобрел скорость \(V_2\), работа, совершаемая силой или силами, оказывающими воздействие на объект, равна увеличению кинетической энергии этого тела.

\(ΔЕ_К = Е_{К2} – Е_{К1}\)

При совпадении векторов сил с направлением движения работа будет иметь положительное значение, а кинетическая энергия будет увеличиваться. В случае, когда сила противоположна движению объекта, будет совершаться отрицательная работа, а тело начнет отдавать кинетическую энергию.

Формул закона сохранения механической энергии

Любой объект, расположенный на высоте, обладает потенциальной энергией. Во время движения при уменьшении высоты данная энергия утрачивается, но не исчезает, а трансформируется в кинетическую энергию этого тела. Если представить груз, закрепленный на какой-то высоте, то в этой точке потенциальная энергия тела будет иметь максимальную величину. При падении груз будет совершать движение с определенной скоростью. Таким образом объект приобретает кинетическую энергию при одновременном уменьшении потенциальной энергии. В точке падения груз будет обладать максимальной кинетической энергией и нулевой потенциальной.

Примеры преобразования потенциальной энергии в кинетическую:

• мяч, сброшенный с высоты, приобретает кинетическую энергию и утрачивает потенциальную;
• во время нахождения санок на вершине горы их кинетическая энергия равна нулю, а при движении ее величина увеличивается, вместе с тем потенциальная энергия уменьшается, но суммарная энергия остается постоянной;
• яблоко, которое висит на дереве, обладает потенциальной энергией, трансформирующейся в кинетическую при его падении.

Данные примеры служат наглядным подтверждением закона сохранения энергии. Согласно справедливому утверждению, полная энергия механической системы — постоянная величина. Она не меняется при перемещении объекта, в то время как потенциальная энергия переходит в кинетическую и наоборот. При увеличении кинетической энергии на определенное значение на такую же величину будет уменьшена потенциальная энергия. Замкнутую систему физических тел можно описать следующей формулой:

\(E_{k1} + E_{п1} = E_{k2} + E_{п2}\)

где \(E_{k1}\), \(E_{п1}\) — значения кинетической и потенциальной энергии до какого-либо взаимодействия, а \(E_{k2}\) , \(E_{п2}\) — соответствующие энергии после взаимодействия.

Явление преобразования кинетической энергии в потенциальную и наоборот можно наблюдать на примере раскачивающегося маятника.

Достигая крайнего правого положения, маятник прекращает движение. В этой точке его высота над поверхностью отсчета будет иметь максимальное значение, как и его потенциальная энергия. Кинетическая энергия тела при этом равна нулю при отсутствии движения. Во время движения маятника вниз его скорость начинает прирастать. В нижней точке кинетическая энергия маятника достигнет максимального значения. Преодолев нижнюю отметку, объект начинает движение вверх в левую сторону. При этом можно наблюдать увеличение потенциальной энергии и уменьшение кинетической.

Исаак Ньютон, демонстрирую трансформацию энергий тела, изобрел механическую систему, которая носит название колыбели Ньютона или шаров Ньютона.

В данной системе при отпускании первого шара энергия и импульс, которыми он обладает, передаются последнему шару, проходя через три промежуточных шарообразных объекта. Данные тела сохраняют неподвижное положение. Последний шар при этом будет отклонен от исходной отметки с такой же скоростью и на такую же высоту, что и первое тело. После завершения движения последнего шара он передаст энергию и импульс с помощью промежуточных шаров первому объекту. Объяснить процесс можно следующим образом:

1. Шар, который отклонили в сторону и зафиксировали, характеризуется максимальной потенциальной энергией.
2. В начальной точке кинетическая энергия этого тела будет равна нулю.
3. Во время движения потенциальная энергия утрачивается, преобразуясь в кинетическую энергию.
4. В моменте столкновения первого шара со вторым его кинетическая энергия будет максимальной, а потенциальная — равна нулю.
5. Через промежуточные шары кинетическая энергия передается к пятому шару.
6. Получая объем кинетической энергии, последнее тело приводится в движение и начинает подъем вверх на высоту, соответствующую высоте, на которой находился первый шар в начальной точке движения.
7. Кинетическая энергия в верхней отметке полностью переходит в потенциальную.
8. При дальнейшем падении происходит передача энергии шарам в обратной последовательности.

Описанный опыт может продолжаться бесконечно при отсутствии неконсервативных сил, которые воздействуют на систему в реальных условиях. Под действием диссипативных сил шары будут утрачивать энергию. Скорость и амплитуда тел будут снижаться. В конце можно наблюдать полную остановку движения объектов. Данный процесс подтверждает справедливость утверждения о том, что закон сохранения энергии работает в условиях отсутствия неконсервативных сил.

Применение закона сохранения механической энергии

Утверждение о неизменности суммы нескольких энергий, которые характерны для определенной системы, актуально в настоящее время. Благодаря открытию закона сохранения энергии, физические дисциплины получили активное развитие, что послужило триггером для инноваций в области науки и техники. К примеру, единство живой природы было детально обосновано с помощью лабораторных практик в процессе исследований закона сохранения механической энергии. Понимание закономерности трансформации одной формы энергии в другую проливает свет на глубину внутренних связей между формами материи. Закон применим к любым явлениям, которые происходят в живой и неживой природе.

Вывод математической записи связи между разными типами движения является одной из важных тем стандартной школьной программы и включен в основы термодинамики. Применение данного соотношения служит ключом к решению распространенных задач единого государственного экзамена. Основные физические правила способны объяснить многие процессы, которые происходят в Солнечной системе и связаны с изменением положения тел в течение определенного промежутка времени. Механическое движение объектов изучают с помощью закона сохранения энергии. Математические исследования существенно упрощаются благодаря постоянству суммарной энергии механической системы.

Примеры разноуровневых задач от простых до сложных, алгоритм решения

Многие задания на закон сохранения энергии требует определения начального и конечного состояния системы. В первую очередь целесообразно представить равнение для начальной энергии системы и сравнить его с конечной. При этом нулевой уровень отсчета потенциальной энергии системы необходимо использовать при записи потенциальной энергии тела.

Задача 1

Необходимо определить высоту подъема тела, которое было подброшено вертикально вверх. Начальная скорость объекта составила 10 м/с. Сопротивление воздуха учитывать не нужно.

Решение

Согласно закону сохранения энергии, значения начальной кинетической энергии и максимальной потенциальной энергии в высшей точке подъема тела будут равны. Записать это утверждение в следующем виде:

\(\frac{mv^{2}}{2}=mgh\)

\(\frac{v^{2}}{2}=gh\)

\(h=\frac{v^{2}}{2g}=\frac{10^{2}}{2*9.81}=5.1\)

Ответ: высота подъема тела составит 5,1 метра.

Задача 2

При сжатии спусковой пружины на 5 см из игрушечного пистолета вылетел шарик. Масса шарика составляет 20 г, а его скорость достигла 2 м/с. Необходимо определить жесткость пружины.

Решение

Согласно закону сохранения энергии потенциальная энергия деформированной пружины преобразуется в кинетическую энергию выпущенного из пистолета шарика. Записать данный процесс можно таким образом:

\(\frac{mv^{2}}{2}=\frac{kx^{2}}{2}\)

\(mv^{2}=kx^{2}\)

\(k=\frac{mv^{2}}{x^{2}}=\frac{0.02*2^{2}}{0.05^{2}}=32H/m\)

Ответ: жесткость пружины составляет 32 Ньютон на метр.

Задача 3

В процессе растяжения на 20 см пружина приобрела потенциальную энергию, характерную для упругодеформированного тела, равную 20 Дж. Необходимо рассчитать жесткость пружины.

Решение

Исходя из формулы, выражающей потенциальную энергию упругодеформированного тела, можно определить жесткость пружины:

\(E=\frac{kx^{2}}{2}\)

\(2E=kx^{2}\)

\(k=\frac{2E}{x^{2}}=\frac{2*20}{(0.2)^{2}}=1000 H/m\)

Ответ: жесткость пружины составляет 1000 Ньютон на метр.

Решение задач по физике любой сложности по силам не только студенту, но и школьнику. Если в процессе обучения все же возникают проблемы, всегда можно обратиться за помощью к Феникс.Хелп.