Уравнение Шредингера для стационарных состояний

Ключевое уравнение квантовой механики предложил Э. Шредингер в 1926 году. Важность данной закономерности сравнима со значением уравнения движения И. Ньютона. Уравнение Шредингера является постулатом. Его справедливость подтверждена результатами реальных экспериментов, проводимых в рамках атомной и ядерной физики.

Стационарное уравнение Шредингера для свободной частицы

Основное положение, выдвинутое ученым, имеет определенный вид. Уравнение Шредингера записывают следующим образом:

\(-\frac{h}{i}\frac{d\Psi }{dt}=-\frac{h^{2}}{2m}\Delta \Psi +U\left(x,y,z,t \right)\Psi \left(1 \right)\)

где \(h=\frac{h}{2}=1.05*10^{-34}\) Дж*с – постоянная Планка,

\(m\) является массой частицы,

U (x, y, z, t) представляет собой потенциальную энергию частицы, которая движется в силовом поле,

\(\Delta =\frac{d^{2}}{dx^{2}}+\frac{d^{2}}{dy^{2}}+\frac{d^{2}}{dz^{2}}\) является оператором Лапласа,

\(\Psi =\Psi (x, y, z, t)\) определяет волновую функцию частицы,

\(i=\sqrt{-1}\) играет роль мнимой единицы.

Данная формула справедлива в отношении любой частицы, перемещающейся со скоростью, которая намного меньше, чем скорость света:

\(v\ll c\)

где с является скоростью света в вакуумной среде.

Существуют некоторые условия, дополняющие уравнение Шредингера, которые реплицируют на волновую функцию \(\Psi (x, y, z, t)\) К таким параметрам относят:

• конечность, непрерывность и однозначность данной функции;
• производные заданной функции \(\left(\frac{d\Psi }{dx},\frac{d\Psi }{dy},\frac{d\Psi }{dz},\frac{d\Psi }{dt} \right)\) отличаются непрерывностью;
• функция \(\left|\Psi \right|^{2}\) интегрируема, то есть ее интеграл должен быть конечным.

Смысл последнего условия заключается в нормировке вероятностей. Это означает, что не сама волновая функция обладает физическим смыслом, а \(\left|\Psi \right|^{2}\). Все перечисленные требования имеют большое значение, так как с их помощью без необходимости решения уравнения Шредингера представляется возможным сделать выводы об энергии и других характеристиках отдельно взятой частицы. В связи с наличием в основной формуле производной от волновой функции по времени, данное уравнение получило название временного.

Уравнения Шредингера для стационарных состояний

В микромире происходит огромное количество явлений. Для многих из этих процессов применима стационарная волновая функция, которая не определяется временем, а также уравнение Шредингера.

Формула справедлива в тех случаях, когда значение потенциальной энергии не определяется временем:

U = U (x, y, z)

Уравнение Шредингера для стационарных состояний будет иметь следующий вид:

\(\Delta \psi +\frac{2m}{h^{2}}\left(E-U \right)\times \psi =0\)

В данном случае для расчетов применяют полную энергию Е. Исходя из теории дифференциальных уравнений, существуют доказательства наличия бесчисленного множества решений вышеуказанной формулы, обладающих физическим смыслом при отборе способом наложения граничных условий. Параметры регулярности волновых функций служат такими условиями:

• волновые функции конечны;
• волновые функции однозначны, непрерывны, наряду с первыми производными.

Решения, определенные регулярными функциями \(\left|\psi \right|\) содержат реальный физический смысл. Они присущи не всем значениям Е, а только конкретным или собственным параметрам по условиям какой-то задачи.

Примеры решения задач для стационарных состояний

Задача 1

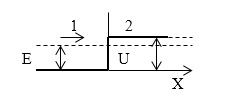
Электронный пучок с энергией Е сталкивается с препятствием в виде барьера высотой U (U > E). Схематично ситуация представлена на рисунке. Необходимо определить относительную вероятность нахождения электрона в области 2, удаленного на расстояние х от границы 1 и 2 областей.

Решение

Вначале необходимо определить, как плотность вероятности нахождения электрона в точке х относится к плотности вероятности его пребывания на границе областей. По условиям задачи предусмотрено наличие высокого потенциального барьера, ширина которого бесконечна. Заряженные частицы будут отражаться от его стенок. Наряду с этим, есть вероятность попадания электрона в область 2. Для того чтобы найти вероятность обнаружения электрона в этой области, следует обратиться к уравнению Шредингера, которое имеет следующий вид:

\(\Delta \psi +\frac{2m}{h^{2}}\left(E-U \right)\times \psi =0\)

В одномерном случае, согласно условиям задачи, уравнение будет преобразовано следующим образом:

\(\frac{d\Psi }{dx^{2}}-\frac{2m}{h^{2}}\left(E-U \right)\Psi =0\)

Решением такого уравнения является функция:

\(\Psi \left(x \right)=Ce^{kx}+De^{-kx}\)

где C и D являются постоянными.

Исходя из того, что при х, который стремится к бесконечности, Ψ тоже стремиться к бесконечности. Такие условия не допустимы, поэтому С = 0. Согласно этому выводу, формула будет иметь следующий вид:

\(\Psi \left(x \right)=De^{-kx}=De^{-\frac{\sqrt{2m(U-E)x}}{h}}\)

Плотность вероятности нахождения частицы в точке х будет рассчитываться следующим образом:

\(p=\left|\Psi \left(x \right) \right|^{2}=D^{2}e^{-\frac{\sqrt[2]{2m(U-E)x}}{h}}\)

На границе плотность вероятности будет следующая:

\(p_{0}=\left|\Psi \left(0 \right) \right|^{2}=D^{2}\)

При таких условиях, относительная вероятность равна:

\(\epsilon =\frac{\left|\Psi \left(x \right) \right|^{2}}{\left|\Psi \left(0 \right) \right|^{2}}=e^{-\frac{\sqrt[2]{2m(U-E)x}}{h}}\)

Ответ: относительная вероятность нахождения электрона в области 2, удаленного на расстояние х от границы 1 и 2 областей будет равна:

\(\epsilon =\frac{\left|\Psi \left(x \right) \right|^{2}}{\left|\Psi \left(0 \right) \right|^{2}}=e^{-\frac{\sqrt[2]{2m(U-E)x}}{h}}\)

Задача 2

Требуется записать уравнение Шредингера для заряженной частицы, которая находится в водородоподобном атоме.

Решение

Прежде чем записать искомое уравнение, необходимо представить формулу расчета потенциальной энергии, которой обладает заряженная частица, включенная в состав водородоподобного атома. Пусть электрон будет находиться на орбите радиуса r.

\(U=-\frac{Zq_{e}^{2}}{4\pi \varepsilon _{0}r}\)

В данном случае следует применить стационарное уравнение для электрона, которое будет записано в следующем виде:

\(\Delta \Psi +\frac{2m_{e}}{h^{2}}\left(E+\frac{Zq_{e}^{2}}{4\pi \varepsilon _{0}r} \right)=0\)

Ответ: уравнение Шредингера для электрона, который находится в водородоподобном атоме, имеет вид:

\(\Delta \Psi +\frac{2m_{e}}{h^{2}}\left(E+\frac{Zq_{e}^{2}}{4\pi \varepsilon _{0}r} \right)=0\)

Благодаря наблюдаемым волновым свойствам частиц, которые описывает уравнение Шредингера, удается исследовать движение микрочастиц в различных силовых полях. Австрийский физик-теоретик совершил настоящий прорыв в области квантовой механики. Студенты современных вузов изучают научные труды Э. Шредингера.

Волновая механика является достаточно сложной в освоении дисциплиной, поэтому, если в процессе обучения возникают трудности, целесообразно обратиться за помощью к сервису Феникс.Хелп.