Закон всемирного тяготения: 4 задачи с решением и ответами
Прошло уже более 300 лет с того времени, как Исаак Ньютон сформулировал этот фундаментальный закон природы. И все эти годы учащиеся разных стран постигали его глубину, упражняясь в решении задач. Предлагаем вашему вниманию 4 примера задач на закон всемирного тяготения.
Задача 1. Расчет расстояния между телами
В разных концах городской площади стоят 2 памятника из гранита. Известно, что масса каждого из них равна 20 тоннам. Также известна сила, с которой они притягиваются друг к другу F = 6,67 •10-5 Н. Найдите расстояние между памятниками.
Решение:
Перед нами классическая задача на применение закона тяготения:
- Даны 2 материальных тела.
- Известна сила, с которой они притягиваются друг к другу.
- Также известны массы этих тел.
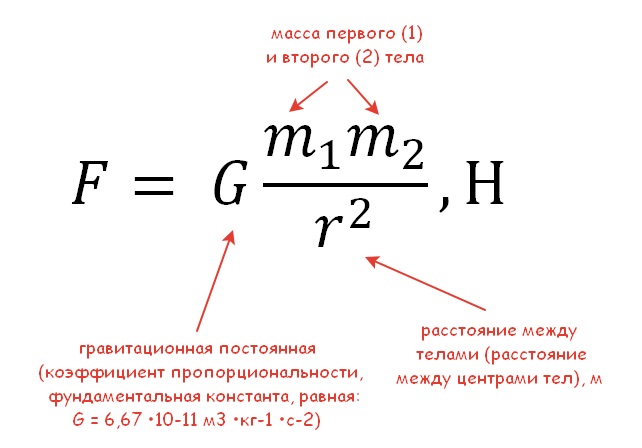
Запишем формулу для вычисления силы:
Преобразуем эту формулу, чтобы найти расстояние между телами:
Подставим числовые значения и получим результат:
Ответ: 20 метров.
Задача 2. Расчет величины ускорения свободного падения на Юпитере
Нужно рассчитать, каково будет ускорение свободного падения на планете Юпитер, если:
- Масса Юпитера равна 1,9 •1027 кг.
- Радиус Юпитера равен 6,9 •107 м.
Решение:
Величина ускорения свободного падения зависит от массы и радиуса планеты, на которой идут измерения. Если тело поднимается над поверхностью, то величина ускорения свободного падения уменьшается. Для каждой планеты она будет различной.
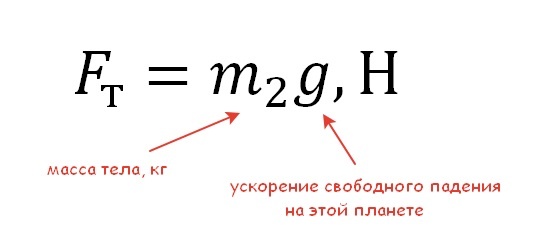
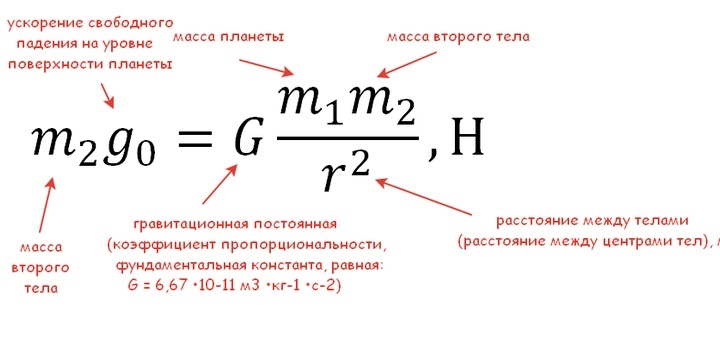
Формула закона всемирного тяготения приведена в первой задаче. С другой стороны, силу тяготения, действующую на какое-либо тело на выбранной планете, мы можем найти благодаря второму закону Ньютона:
Запишем данный факт в виде:
Сократим в левой и правой части m2 и получим:
Так выглядит формула для расчета ускорения свободного падения на рассматриваемой планете.
Подставим числовые значения и получим результат:
Ответ: 24,79 м/с2.
Задача 3. Первая космическая скорость для Марса
Нужно найти первую космическую скорость для Марса, если:
- Масса Марса равна 6,4 •1023 кг.
- Радиус Марса равен 3,4 •106 м.
Решение:
Если тело будет подниматься над поверхностью планеты и достигнет при этом первой космической скорости, то оно будет испытывать силу притяжения этой планеты, двигаться по орбите вокруг нее и не сможет улететь с этой орбиты, но и не упадет обратно на её поверхность. Такое тело становится спутником планеты. Чтобы тело смогло преодолеть силу притяжения планеты и улететь в межзвездное пространство, ему необходимо набрать более высокую скорость, называемую второй космической скоростью. Для планеты Земля значение первой космической скорости равно 7,91 км/с, а значение второй — 11,2 м/с.
Найдем значение первой космической скорости для Марса по формуле:
Подставим числовые значения и получим результат:
Ответ: 3,6 м/с.
Задача 4. Изменение ускорения свободного падения (УСП) в зависимости от высоты над поверхностью
Самолет поднимается на 6 км. На сколько изменится при этом величина УСП для тел, находящихся в самолете? Радиус Земли равен 6,371 •103 м, а УСП на уровне поверхности принять равным 9,81 м/с2.
Решение:
Как известно, УСП уменьшается по мере подъема над поверхностью планеты. И постепенно становится неизмеримо малым. Вычислить УСП на разных высотах поможет формула закона всемирного тяготения. Запишем эту формулу для двух случаев.
Первый случай — на уровне поверхности планеты с учетом второго закона Ньютона:
Второй случай — над поверхностью планеты на высоте «h»:
Где g1 — ускорение свободного падения над поверхностью планеты на высоте «h», м/с2.
Отсюда мы можем записать отношение:
Подставим числовые значения и получим результат:
То есть, величина УСП на высоте 6 км будет в 1,002 раза меньше, чем над поверхностью.
Тогда величина ускорения свободного падения на высоте 6 км будет равна:
Найдем разность ускорений свободного падения на разных высотах:
g0 – g1 = 9,81 – 9,79 = 0,02 м/с2.
Ответ: на высоте 6 км величина ускорения свободного падения уменьшится на 0,02 м/с2.
Наш разбор типовых задач на закон всемирного тяготения подошел к концу. Если ваше задание не подходит ни под один из примеров, рекомендуем обратиться к специалистам ФениксХелп: они найдут решение и с радостью помогут справиться с любой учебной работой.
Понравилась статья?
Подпишитесь на наш блог и получайте наши статьи первым!
Или подписывайтесь на нас в соцсетях:
Заметили ошибку? Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так

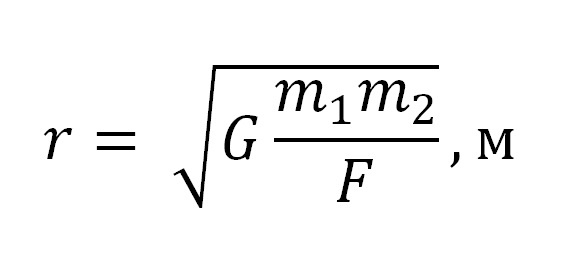
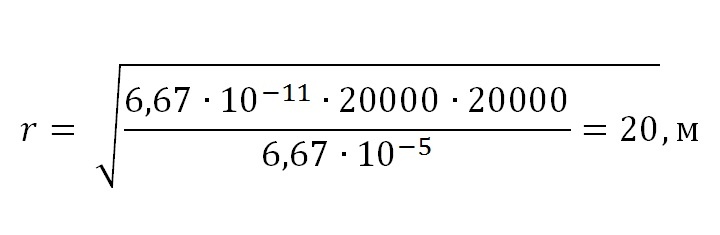
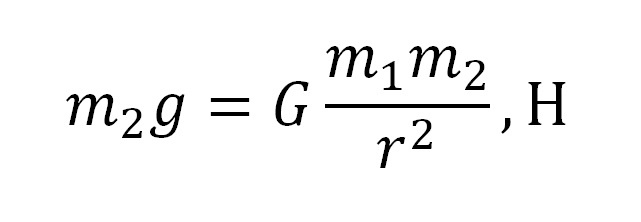
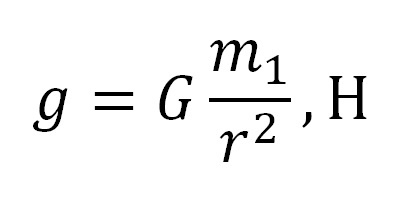
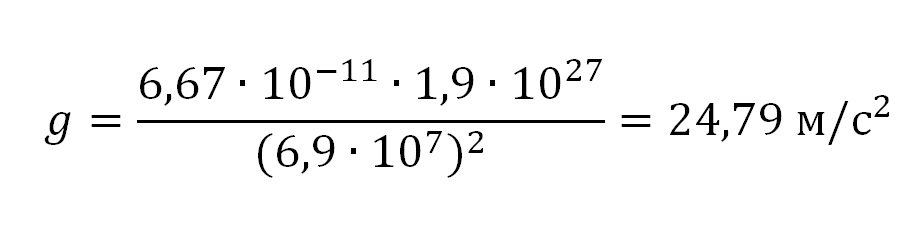
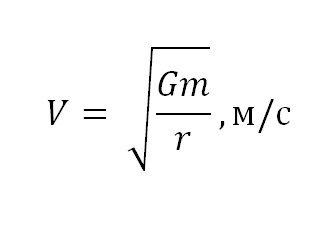
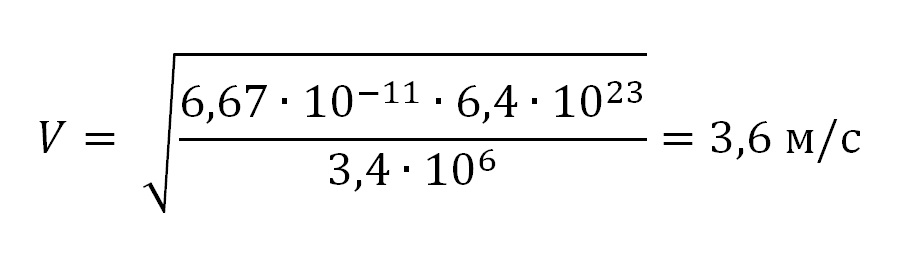
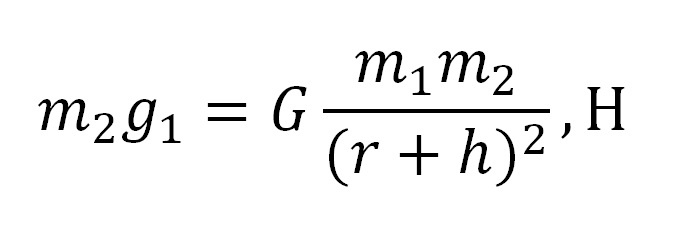
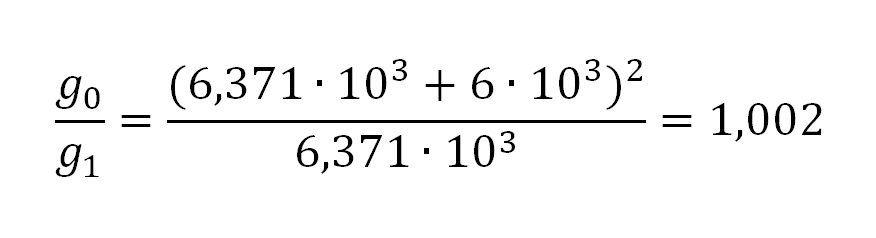
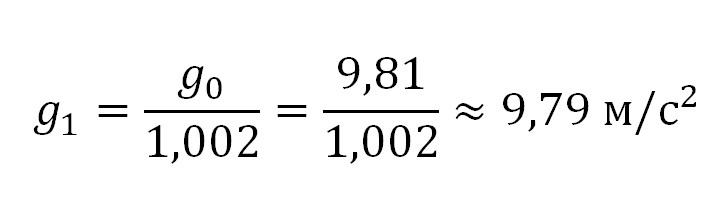
Бесплатно отвечаем на ваши вопросы. Задайте свой вопрос и получите ответ от профессионального преподавателя. Выберите лучший ответ.
Вопросы могут задавать только авторизованные пользователи. Войти