Что называется колебательным контуром
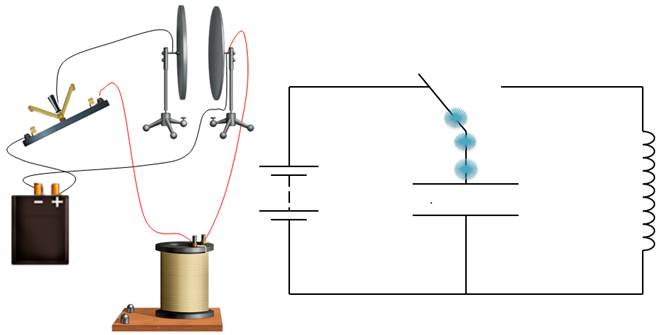
Типичным примером свободных колебаний являются пружинные механизмы или математический маятник. Однако в результате многочисленных опытов удалось настроить подобные системы не только в механических установках, но и в электрических цепях. К таким цепям относится колебательный контур.
Что такое колебательный контур, из каких элементов состоит
Колебательный контур является простейшей системой, для которой характерно образование свободных электромагнитны колебаний.
Колебательный контур представляет собой электрическую сеть. В состав замкнутого контура входят следующие компоненты:
- конденсатор;
- катушка;
- резистор.
В цепи образуются свободные затухающие колебания электромагнитного характера. В зависимости от силы сопротивления резистора определяется скорость затухания колебаний.
Идеальным колебательным контуром называют колебательный контур с полным отсутствием электрического сопротивления. Для такой системы характерны незатухающие свободные электромагнитные колебания.
Области применения резонансных контуров достаточно широки. Они необходимы для изготовления полосовых и режекторных фильтров в усилителях, радиоприемниках и устройствах автоматики.
Колебательные контуры являются компонентами блоков измерения частоты, которые устанавливаются на самолетах марки Ил-62М, Ил-76 и Ту-154М. С их помощью контролируется постоянная частота напряжения на генераторе при изменениях количества оборотов двигателя.
Виды колебательных контуров
Последовательным колебательным контуром называют цепь, в состав которой входит катушка индуктивности и конденсатор, соединенные последовательно. Идеальный последовательный колебательный контур характеризуется несколькими величинами:
- L – индуктивность, Гн;
- С – емкость, Ф.
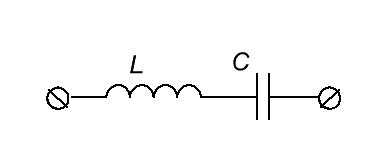
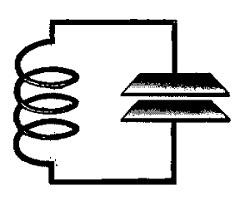
На рисунке изображен идеальный последовательный контур.
В отличие от вышеуказанного идеального колебательного контура реальный последовательный контур обладает сопротивлением потерь катушки и конденсатора. Сумма величин этих сопротивлений обозначается буквой R.
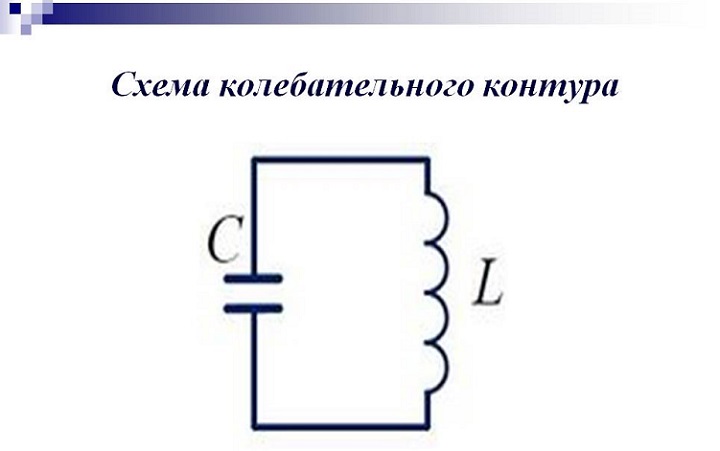
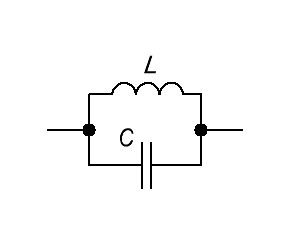
Характеристиками параллельного идеального колебательного контура, как и в первом случае, являются индуктивность и емкость. На рисунке представлена схема такой цепи.
В реальном колебательном контуре катушка за счет наличия проводниковой намотки обладает неким сопротивлением потерь, как и конденсатор. Емкостные потери небольшие, что позволяет не учитывать их во многих расчетах.
Закон сохранения энергии в колебательном контуре, формула
Рассмотреть колебательный контур можно на примере идеальной модели с конденсатором, емкость которого обозначается \(С\), и катушкой, характеризующейся индуктивностью \(L\). Исходя из особенностей идеального контура, в нем отсутствуют потери энергии. Во время колебательных движений энергия электрического поля \(WC\) преобразуется в энергию магнитного поля \(WL\) и наоборот. Представить этот процесс можно в виде формулы:
\(W = WC(t) + WL(t) = const\)
Максимального значения энергия достигает при максимальном значении заряда \(q\). Данное соотношение можно представить с помощью уравнения:
\(W_{Cmax}= \frac{q^{2}max}{2C}\)
В этом случае наблюдается нулевое значение энергии магнитного поля в катушке индуктивности, то есть ток равен нулю.
Для того чтобы весь объем электрической энергии трансформировался в энергию магнитного поля, необходимо иметь в контуре ток \(I\) максимального значения. Данное отношение описывается формулой:
\(W_{Lmax}= \frac{LI^{2}max}{2}\)
Тогда энергия электрического поля и заряд на конденсаторе будут равны нулю.
При таких условиях можно вывести следующее соотношение:
\(W_{Lmax}= \frac{LI^{2}max}{2}= \frac{q^{2}max}{2C}= W_{Cmax}\)
\(Imax = ωqmax\)
Период колебаний, от чего зависит
Определить периодичность свободных колебаний в условиях колебательного контура можно с помощью формулы Томпсона. Уравнение выглядит следующим образом:
\(T=2\pi\sqrt{LC}\)
- \(T\)T обозначает период колебаний и выражается в секундах;
- \(L\)- величина индуктивности, обозначается Гн (Генри);
- \(С\) используют для измерения электроемкости конденсатора, в Ф (Фарад);
- \(π\) – константа, равная 3,14.
Явление резонанса тока в колебательном контуре
Электромагнитные колебания в колебательном контуре характеризует определенная частота. Данная величина называется резонансом.
Частота колебаний зависит от нескольких параметров колебательного контура:
- емкость конденсатора \(C\);
- индуктивность катушки \(L\);
- сопротивление резистора \(R\).
Формула для расчета частоты колебаний выглядит следующим образом:
\(f = \frac{1}{2\pi\sqrt{LC}}\)
Преобразование разных типов энергии с помощью колебательного контура нашло применение в разных областях электротехники и механики. Подобные дисциплины изучают студенты высших и профессиональных учебных заведений, чтобы потом применять их для реализации разнообразных инженерных проектов. Оперативную и компетентную помощь в процессе обучения можно получить на портале Феникс.Хелп.
Понравилась статья?
Подпишитесь на наш блог и получайте наши статьи первым!
Или подписывайтесь на нас в соцсетях:
Заметили ошибку? Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так


Бесплатно отвечаем на ваши вопросы. Задайте свой вопрос и получите ответ от профессионального преподавателя. Выберите лучший ответ.
Вопросы могут задавать только авторизованные пользователи. Войти