Математика в искусстве: живопись
Многие люди относят себя к «гуманитариям» или «технарям», отметая важность противоположного течения. В цикле статей «Математика в искусстве» мы покажем, что точные и гуманитарные науки тесно связаны, а также расскажем об их влиянии друг на друга.
Красота математики
Прежде чем перейдем к основной теме статьи — живописи, расскажем, почему математика и искусство неразрывно связаны.
Произведения музыки, поэзии, театра и кинематографа относят к категории прекрасного, но можно ли сказать то же самое о математике? Ее восприятие как объекта эстетического наслаждения обозначают понятием «красота математики». Гармония чисел и форм, методы решений, закономерности и пропорции — предмет восхищения ученых и любителей науки. Британский философ и математик Бертран Рассел сказал:
Правильный взгляд на математику открывает не только истину, но и безупречную красоту — холодную и суровую, лишенную вычурных уловок, — совершенство великого искусства
Математические измерения и формы повлияли на музыкальные ритмы, архитектурные и изобразительные композиции, помогли добиться реалистичного отображения жизни в искусстве. Вспомним «Витрувианского человека» да Винчи: математические пропорции человеческого тела полностью изменили представления художников об изображении людей.
С чего все начиналось
Художники античности практически не прибегали к использованию перспективы. Вместо правильного изображения объектов на плоскости творцы выделяли более тематически значимые предметы и привлекали внимание к определенным фигурам.
Начиная с эпохи Возрождения, математика все больше затрагивала сферы изучения природы и искусства. С этим связана и заинтересованность художников точной наукой. Во-первых, они хотели добиться правильного размещения объектов на рисунке. Во-вторых, многие философы и деятели искусств верили, что математика — истинная суть мира, и все подчинено геометрическим законам.
Итальянский художник и архитектор эпохи Проторенессанса Джотто ди Бондоне был одним из первых, кто начал применять законы перспективы в работах.
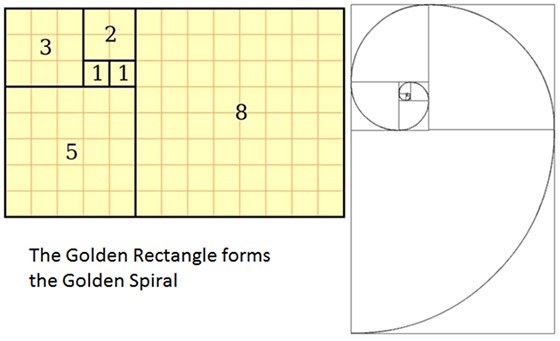
Золотое сечение
Золотым сечением называют уникальную пропорцию красоты, которую используют для большей выразительности произведений искусства
Если говорить научным языком, то золотое сечение — это отношение между частями целого, при котором меньшее относится к большему так же, как и большее к целому.
Присмотревшись к «золотой спирали» ближе, можно заметить, что ее структура напоминает ряд чисел Фибоначчи — последовательность, где каждое следующее число равно сумме двух предыдущих:
- 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55…
Так как изобразить ноль графически нельзя, рисование начинается с квадрата со стороной 1.
Для более гармоничной композиции правило золотого сечения применяют в живописи, фотографии, дизайне, архитектуре, скульптуре и даже музыке. Пропорция позволяет выстроить объекты правильно с точки зрения эстетики.
В картинах
Леонардо да Винчи применял золотое сечение в своем творчестве наиболее часто. Также именно он продемонстрировал связь между человеческим телом и Божественной пропорцией.
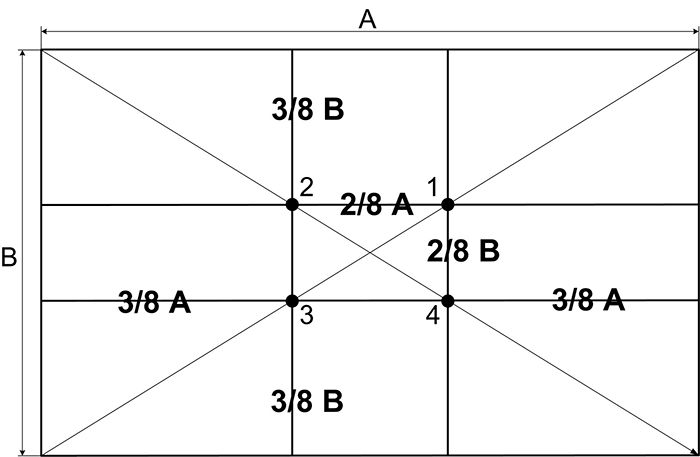
Золотое сечение задает направление художникам, указывает, где должны располагаться первостепенные и второстепенные фигуры, помогает создать композицию. Но Архимедову спираль, которую мы продемонстрировали выше, можно наблюдать в картинах не всегда. Творцы пользуются и другими принципами сечения:
На картинке выше можно наблюдать упрощенное правило золотого сечения, «правило третей». Изображение условно делится на 3 части по горизонтали и вертикали, образуя 9 ячеек и 4 точки пересечения по центру. Именно эти точки привлекают человеческий глаз в первую очередь, и только после того как мы взглянем на них, обращаем внимание на остальные предметы картины.
Узнать больше о золотом сечении и о том, как развивалась идея, можно из видео:
Фракталы
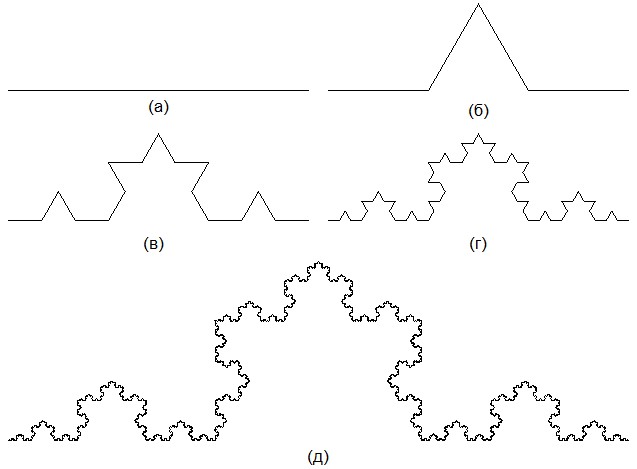
Фрактальные структуры — повторяющиеся части множества, обладающие свойством самоподобия.
Как и золотое сечение, фракталы часто встречаются в природе. Их можно увидеть в облаках, снежинках, кронах деревьев и растениях. В математике одним из самых распространенных примеров фрактала является кривая Коха, которая состоит из повторяющихся сегментов.
В произведениях живописи фракталы встречаются нечасто, по крайней мере, в математическом понимании. Скорее, создание некоторых элементов картин основано на фрактальных структурах, но в точности не повторяет их.
Одним из ярчайших примеров применения фракталов в живописи является гравюра японского художника Кацусики Хокусая «Большая волна в Канагаве».
Мы рассказали об основных математических принципах, которые применялись и применяются в изобразительном искусстве. А о том, как эта точная наука повлияла на другие сферы творчества, вы узнаете из следующих статей цикла.
Не вешайте на себя ярлык «технарь» или «гуманитарий», развивайтесь во всех направлениях. А если появятся трудности в учебе, обращайтесь к специалистам Феникс.Хелп. Здесь всегда рады помочь.
Понравилась статья?
Подпишитесь на наш блог и получайте наши статьи первым!
Или подписывайтесь на нас в соцсетях:
Заметили ошибку? Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так








Бесплатно отвечаем на ваши вопросы. Задайте свой вопрос и получите ответ от профессионального преподавателя. Выберите лучший ответ.
Вопросы могут задавать только авторизованные пользователи. Войти