Примеры решения задач при равноускоренном движении

Разбираемся с понятием равноускоренного движения в физике и рассматриваем его применение на практике в решении задач.

Что такое равноускоренное движение в физике

Равноускоренное движение — это движение, у которого скорость постоянно изменяется, но ускорение является константной (неизменной) величиной. То есть a=const.

Например, если с высотного здания сбросить гирю (или любой другой тяжелый предмет) она будет лететь на землю с ускорением свободного падения. Разгоняющийся с нуля до 60 км/ч автомобиль будет иметь a равное 1 метр на секунду в квадрате.

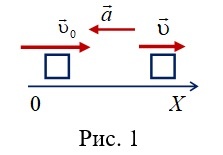
При этом, постепенная остановка тоже может быть примером такого движения. Единственное отличие состоит в том, что векторы скорости и ускорения направлены в разные стороны. Например, вектор a постепенно останавливающегося поезда будет направлен в противоположную сторону от его изначальной скорости.

Обычно в решении задач на данного вида движение применяют всего пять величин: проекции перемещения \(S_x\), проекции скорости \(V_x\), проекции ускорения \(a_x\) и времени \(t\). Зная лишь три из них, вы сможете без особых усилий найти остальные.

Также при решении задач подобного рода применяют два различных способа вычислений в зависимости от уже известных в условии величин.

Способы вычисления

Способ 1

Согласно этому способу, для решения любых задач нам понадобится лишь 2 основных формулы:

\(V_x=V_{0x}+a_x\cdot t и\)

\(S_x=V_{0x}\cdot t+\frac{a_x\cdot t^2}2\)

Бывает, попадаются задачи, когда обе эти формулы приходится объединять в систему. Это бывает в тех случаях, когда нам неизвестны сразу две величины.

Способ 2

В этом случае нужно будет запомнить целых 5 формул. Но помимо того, что их надо запомнить, необходимо уметь применять эти уравнения на практике в решении задач:

1. \(V_x=V_{0x}+a_x\cdot t\) (нет величины \(S_x\)).
2. \(S_x=V_{0x}\cdot t+\frac{a_x\cdot t^2}2\) (отсутсвует \(V_x\)).
3. \(S_x=V_x\cdot t-\frac{a_x\cdot t^2}2\) (нет \(V_{0x}\)).
4. \(S_x=\frac{{V^2}_x-{V^2}_{0x}}{2a_x}\) (нет \(t\)).
5. \(S_x=\frac{V_x+V_{0x}}2\cdot t\) (отсутствует \(a_x\)).

Задачи на равноускоренное прямолинейное движение

Теперь потренируемся в применении полученных знаний из теории и решим несколько задач на равноускоренное прямолинейное движение.

Задача 1

Известно, что некое тело прошло путь 20 м за 2 с прямолинейного равноускоренного движения. При этом оно увеличило свою скорость в n=3 раза. Необходимо найти конечную скорость этого объекта.

Решение:

Пусть скорость тела была \(V_0\), тогда через 2 с она стала равна \(V=3V_0\). Так как из задания мы знаем путь, который прошел данный объект, мы можем найти его a по формуле:

\(V^2-{V^2}_0=2aS\)

\(a=\frac{V^2-{V^2}_0}{2S}=\frac{8{V^2}_0}{2S}=\frac{4{V^2}_0}S.\)

Таким образом, пройденное телом расстояние можно записать следующим образом:

\(S=V_0t+\frac{4{V^2}_0t^2}{2S}=V_0t+\frac{2{V^2}_0t^2}S.\)

Решим квадратное уравнение относительно \(V_0\):

\(\frac{2{V^2}_0t^2}S+V_0t-S=0\)

\(D=t^2+4S\frac{2t^2}S=9t^2\)

\(V_0=\frac{(-t+3t)S}{4t^2}=\frac S{2t}=\frac{20}{2\cdot2}=5\) м/с.

Через 2с его скорость будет равна \(3V_0=3\cdot5=15\) м/с —это будет конечная искомая скорость объекта.

Ответ: 15 м/с

Задача 2

Поезд тормозит с a равным \(0,2м/с^2\). На каком расстоянии от места начала действия тормоза скорость поезда станет равной 5 м/с, если перед торможением она была равна 15 м/с?

Решение:

Так как скорость поезда уменьшается, ускорение направлено в противоположную сторону от его начальной скорости. При прямолинейном движении перемещение поезда равно расстоянию, которое он пройдет.

Ось 0Х направлена в одну сторону с начальной скоростью, поэтому справедливо: \(S_x=S, V_x=V, V_{0x}=V, a_x=-a\).

Используем уже известное нам уравнение \(V_x=V_{0x}+a_x\cdot t\), из которого выражаем время:

\(t=\frac{V_x-V_{0x}}{a_x}=\frac{V-V_0}{-a}=\frac{5-15}{-0,2}=\frac{-10}{-0,2}=50\) с.

t=50 с.

Для определения пути используем формулу \(S_x=V_{0x}\cdot t+\frac{a_x\cdot t^2}2\).

\(S=V_0\cdot t-\frac{a\cdot t^2}2=15\cdot50-\frac{0,2\cdot50^2}2=750-250=500\) м.

Ответ: 500 м.

Задача 3

Хоккейная шайба проскользила по льду за 2,5 с расстояние равное 50 м и остановилась. Выяснить, с каким ускорением двигалась шайба.

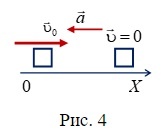
Решение:Так как шайба остановилась, ее конечная скорость будет равна V=0. Как и в предыдущей задаче, скорость шайбы постепенно уменьшается, следовательно, ускорение будет направлено против движения. Расстояние, которое пройдет шайба за время своего торможения — это длина поля: S=l. Расположим значения на оси 0X: \(S_x=l, V_x=0, V_0x=V_0, a_x=-a. \)

Эту задачу не так-то просто будет решить по действиям, потому что в каждом уравнении окажутся неизвестными сразу две величины. Таким образом, придется решать систему уравнений:

\(\left\{\begin{array}{l}S_x=V_{0x}\cdot t+\frac{a_x\cdot t^2}2\\V_x=V_{0x}+a_x\cdot t\end{array}\right.\)

\(\left\{\begin{array}{l}l=V_0\cdot t-\frac{a\cdot t^2}2\\0=V_0+a\cdot t\end{array}\right.\)

Из этого получаем:

\(V_0=a\cdot t\)

\(l=a\cdot t\cdot t-\frac{a\cdot t^2}2=\frac{a\cdot t^2}2\)

\(a=\frac{2l}{t^2}=\frac{2\cdot50}{6,25}=\frac{2\cdot50\cdot4}{25}=16 м/с^2.\)

Ответ: \(16м/с^2.\)

Если все равно ничего не понятно или просто нет времени на написание работы, обращайтесь в ФениксХелп. Опытные специалисты помогут решить задачу любой сложности.