Решение задач на кинетическую и потенциальную энергию

Энергия является важнейшим понятием в механике. Данный термин определяет способность тела совершать работу. Универсальная количественная мера в физике характеризует движение и взаимодействие объектов. Она может быть двух типов: потенциальной и кинетической.

Потенциальная и кинетическая энергия

Определить потенциальную энергию тела можно, зная его массу, ускорение свободного падения и положение относительно земли. Формула для расчета имеет следующий вид:

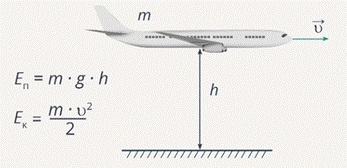
E = m * g * h

В международной системе СИ потенциальная энергия обозначается буквой Е и измеряется в Дж (Джоуль).

В вышеуказанной формуле m является массой тела, h представляет собой высоту, а g – ускорением свободного падения, которое приблизительно равно 9,8 м/с2.

Величина потенциальной энергии определяется выбранной системой отсчета. Это связано с тем, что отсчет высоты можно выполнять не только относительно земной поверхности, но и от какой-то точки или определенного уровня.

Кинетическая энергия служит для определения запаса энергии тела, обладающего определенной скоростью. Определить кинетическую энергию можно с помощью формулы:

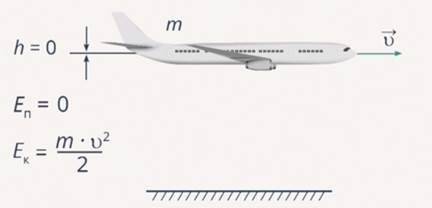
\(E=\frac{mv^{2}}{2}\)

В международной системе СИ кинетическая энергия обозначается буквой Е и измеряется в Дж (Джоуль).

В уравнении m является массой тела, а v представляет собой его скорость.

Скорость тела определяется выбранной системой отсчета. Поэтому кинетическая энергия также зависит от того, каким образом рассчитывают характеристики системы, в которой движется тело.

Каким законам подчиняется, формулы

Потенциальная энергия характерна не только для тела, находящегося на определенной высоте. Несколько иначе выполняют расчет потенциальной энергии упруго деформированного тела. При деформации изменяется его форма и объем, при этом объекту передается определенный запас энергии. К примеру, если растянуть пружину или, напротив, сжать ее, то такие действия меняют расстояние, на которое удалены атомы и молекулы друг от друга. Таким образом, создается потенциальная энергия.

Расчет потенциальной энергии деформированного объекта выполняют с помощью уравнения:

\(E=\frac{k(\Delta x)^{2}}{2}\)

k является жесткостью пружины, \(\Delta x\) — это изменение длины пружины.

Следует отметить, что значение потенциальной энергии пружины будет всегда положительным, так как формула содержит ее изменение в квадрате. Даже в случае, когда изменение будет иметь знак «-», потенциальная энергия в любом случае останется положительной.

Говоря об энергии, следует учитывать, что объект обладает несколькими типами энергии одновременно. К примеру, летящий на большой высоте самолет имеет запас потенциальной энергии, так как удален от поверхности земли, и кинетической энергии из-за своей скорости движения.

Ели принять земную поверхность за уровень нулевой энергии, то данное утверждение будет справедливо. В случае, когда рассматривают объект в других системах отсчета, его энергия будет отличаться.

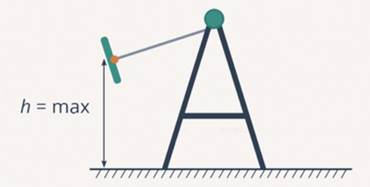
Рассматривая качели, можно сказать, что они обладают запасом и кинетической, и потенциальной энергии. Когда конструкция максимально отклоняется от равновесного положения, энергия будет рассчитываться таким образом:

Е_п = макс

Е_к = 0, так как скорость имеет нулевое значение.

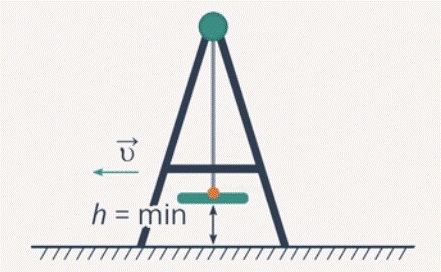
В момент, когда качели пересекают точку равновесного положения, энергия будет распределена следующим образом:

Е_к = макс

скорость качелей в этой точке будет максимальна;

Е_п = мин

высота, на которой тело находится над землей, будет минимальной.

При сложении двух видов энергии получают полную механическую энергию тела. Она включает потенциальную и кинетическую энергии.

Задачи по теме с подробными решениями

Задача 1

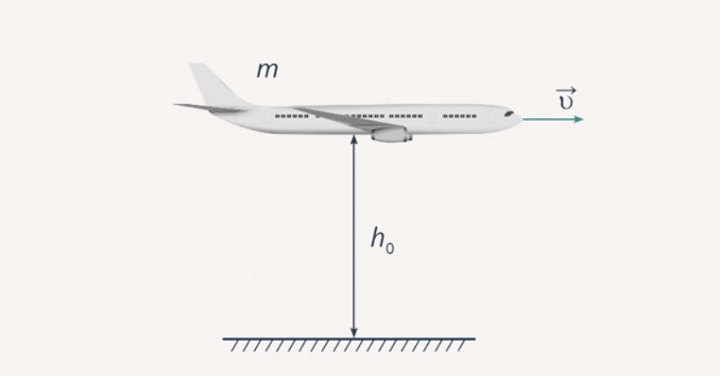
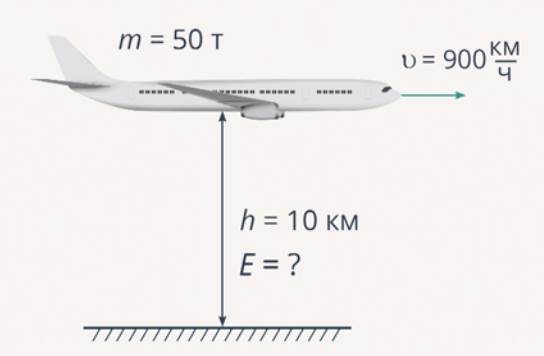
Самолет, масса которого составляет 50 тонн, пролетает на высоте 10 километров. Скорость транспортного средства равна 900 км/ч. Требуется рассчитать, какова полная механическая энергия самолета.

Решение

Первым шагом является перевод искомых данных, согласно системе СИ. В таком случае масса самолета составит 50 000 кг, скорость – 250 м/с, а высота – 10 000 м.

Самолет обладает запасом полной энергии, которая включает и потенциальную, и кинетическую.

E = E_п + Е_к

E_п = m * g * h

Е_к = m * v² / 2

Таким образом, полная энергия составит:

\(E=m\times g\times h\times \frac{mv^{2}}{2}\)

Если подставить в полученную формулу числовые значения величин из условия задачи, то получим полную энергию:

\(E=6.5625\times 10^{9}\) Дж

Если записать ответ сокращенно, то он примет такой вид:

\(Е = 6,5625\) Гдж.

Ответ: в рассмотренной системе отсчета значение полной механической энергии самолета составит 6.5625 Гдж.

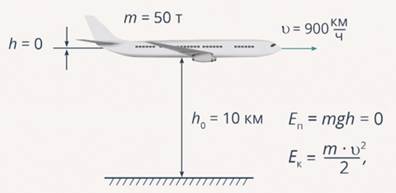
Однако, данную задачу можно решить, принимая за нулевой уровень отметку в 10 километров. Тогда транспортное средство будет характеризоваться лишь запасом кинетической энергии, а значение потенциальной энергии будет равно нулю.

Задача 2

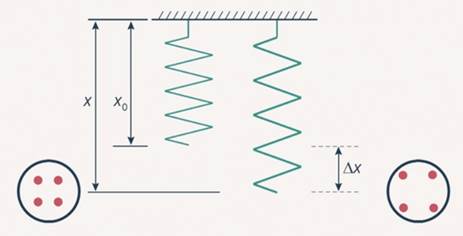
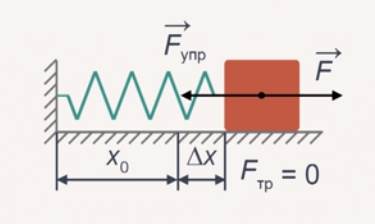
Пружину закрепили к стене и поместили на гладкую поверхность. На конце пружины зафиксировали тело. Растяжение пружины, которая обладает жесткостью в 400 Н/м, происходит при воздействии силы в 80 Н. Требуется рассчитать запас энергии в пружине.

Решение

Согласно условию задачи, поверхность обладает гладкостью, что позволяет сделать вывод о нулевом значении силы трения. Таким образом, потери энергии исключены. Воздействуя на пружину, можно наблюдать ее деформацию. Весь запас энергии будет сосредоточен в ней. Найти данную величину можно по формуле:

\(E=\frac{k(\Delta x)^{2}}{2}\)

Сила упругости равна произведению жесткости на изменение длины пружины:

\(k\times \Delta x=F\)

Деформацию пружины можно рассчитать таким образом:

\(\Delta x=\frac{F}{k}\)

Используя последнее равенство, можно преобразовать формулу для расчета энергии:

\(E=\frac{k(\frac{F}{k})^{2}}{2}=\frac{kF^{2}}{2k^{2}}=\frac{F^{2}}{2k}\)

Далее следует подставить числовые значения в полученное выражение:

\(E=\frac{80^{2}}{2\times 400}=8\) Дж

Ответ: запас энергии в пружине составляет 8 Дж.

Задача 3

Масса пули составляет 9 грамм. Ее выпустили из оружия вертикально в верхнем направлении. Скорость пули при этом составила 700 м/с. Требуется рассчитать ее кинетическую энергию.

Решение

Условия задачи удобно представить в виде рисунка.

Расчет нужно выполнить по формуле:

\(E=\frac{mv^{2}}{2}\)

Перед тем, как подставить в уравнение числовые значения, требуется перевести их в систему СИ. Тогда масса пули составит 0,009 кг. Выражение будет записано следующим образом:

\(E=\frac{0.009\times 49\times 10^{4}}{2}=2200\) Дж

Ответ: запас кинетической энергии пули равен 2200 Дж.

Задача 4

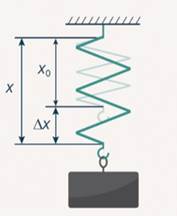
Масса ракеты составляет 0,2 кг. Ее выпустили из орудия вертикально вверх. После этого ракета достигла высоты в 60 метров. Требуется рассчитать значение потенциальной энергии ракеты, характерной для этой отметки.

Решение

Условие задачи можно представить с помощью рисунка.

Для того чтобы рассчитать потенциальную энергию, требуется воспользоваться формулой:

E = m * g * h

Далее необходимо подставить в выражение числовые значения:

Е = 0,2 * 9,8 * 60 = 118 Дж

Ответ: потенциальная энергия ракеты на заданной высоте составит 118 Дж.

Задача 5

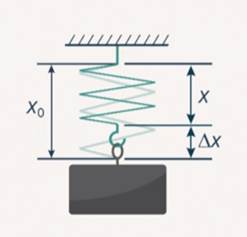
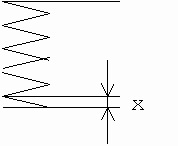
Пружину растянули на 5 мм. Коэффициент ее жесткости составляет 10000 Н/м. Требуется вычислить, какова энергия пружины.

Решение

Следует представить условия задачи на рисунке.

Уравнение, с помощью которого можно рассчитать энергию пружины, имеет такой вид:

\(E=\frac{k(\Delta x)^{2}}{2}\)

Далее необходимо привести к системе СИ расстояние, на которое растянули пружину. Оно составит 0,005 м.

После преобразований можно подставить числовые значения в искомую формулу:

\(E=\frac{10^{4}\times 25\times 10^{-6}}{2}=0.125\) Дж

Ответ: энергия пружины составляет 0,125 Дж.

Знание основных формул для расчета кинетической, потенциальной и полной энергии тела позволит решить задачи любой сложности. Наиболее простым способом является выполнение последовательных действий, включая запись условий задачи, графическое изображение системы, представление формул для вычисления энергии, решение уравнения с помощью подстановки числовых значений. Важно отметить, что механическая энергия представляет собой сумму потенциальной и кинетической энергии.

Если в процессе поиска решений уравнений возникают трудности, всегда можно обратиться за помощью к сервису Феникс.Хелп.