Свойства определителя матрицы и его нахождение
Матрица в математике — это таблица упорядоченных взаимосвязанных элементов, состоящая из m-строк и n-столбцов. В квадратной матрице m=n, то есть A = (n×n). Одной из основных ее характеристик, применяемых в решении большинства задач, является определитель.
Определитель матрицы — что это такое, его свойства
Точного определения этого термина не существует, однако для понимания:
Определитель — это некоторая скалярная величина, с которой можно сопоставить любую квадратную матрицу.
Три альтернативных обозначения: |А|, Δ, det A. Методы вычисления варьируется в зависимости от порядка матрицы (количества строк или столбцов).
Что называют детерминантом
При изучении матричного определителя часто мелькает латинское слово «детерминант». На самом деле, разницы нет — это одно и то же понятие. Однако детерминант имеет множество значений в других областях науки, поэтому в математике чаще всего используют его русский перевод.
Расстановка индексов в матрице
Индексы — это координаты элемента в системе. У каждого элемента их два: первый указывает на строку, второй — на столбец.
Поскольку порядок — это количество строк или столбцов в квадратной матрице, то его можно определить по m-индексу нижней строки или n-индексу крайнего правого столбца. Такой способ применяется в том случае, если таблица очень большая и считать строки (столбцы) неудобно.
Алгебраическое определение
Алгебраический смысл таков:
Определитель матрицы А = (n×n) — это алгебраическая сумма n слагаемых.
Формула:
Каждое слагаемое — это произведение n-элементов, взятых по одному из каждой строки и каждого столбца, умноженное на (-1) в степени Np (количество инверсий).
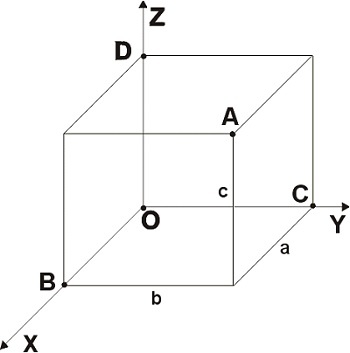
Геометрическое определение
Геометрический смысл таков:
Определитель — это объем параллелепипеда, который получается, если рассмотреть строки в качестве векторов, образующих ребра.
Еще раз: количество строк (столбцов) равно количеству векторов. Таким образом, если нам дана матрица А = (2×2), то она является двухмерным параллелограммом, а детерминант — площадью данной фигуры. Если А = (3×3), то это трехмерный параллелепипед, а определитель — его объем.
Общая схема вычисления определителей
Для матрицы 1-го порядка определитель равен его единственному элементу:
\(|a_{11}| = a_{11}\)
Для 2-го порядка — произведение элементов главной диагонали минус произведение побочной.
\(|а_{11} а_{12}|\)
\(|а_{21} а_{22}| = а_{11} * а_{22} — а_{12} * а_{21}\)
Для нахождения А = (3×3) есть два способа:
- правило треугольника;
- правило Саррюса.
Правило треугольника выглядит следующим образом:
Если показывать графически, то:
По правилу Саррюса нужно:
- Дописать слева от определителя два первых столбца.
- Перемножить элементы главной диагонали и параллельных диагоналей, взяв произведения со знаком «+».
- Перемножить элементы побочных диагоналей и параллельных им, взяв произведения со знаком «–».
Матрицы от 4-го порядка считают разложением строк или столбцов, но такой метод применяется редко и требует знаний об алгебраическом дополнении и миноре.
Вычисление определителя матрицы, примеры с решением
Задача №1: вычислить детерминант матрицы A = (n×n), равной
| 11 -3 |
| 15 -2 |.
Решение:
\(|а_{11} а_{12}|\)
\(|а_{21} а_{22}| = а_{11} * а_{22} — а_{12} * а_{21}\), следовательно
det A = 11 * (-2) – (-15) * (-3) = (-22) – 45 = (-67)
Ответ: det A = (-67)
Задача №2: определить det A матрицы, равной
| 1 3 4 |
| 0 2 1 |
| 1 5 -1 |
Решение: если методом треугольника, то:
Следовательно:
det A = (1 * 2 * (-1) + 3 * 1 * 1 + 0 * 5 * 4) — (4 * 2 * 1 + 3 * 0 * (-1) + 1 * 5 * 1) =
((-2) + 3 + 0) — (8 + 0 + 5) = 1 — 13 = (-12)
Ответ: det A = (-12)
Сложно? Феникс.Хелп может помочь в решении домашних, самостоятельных и контрольных работ.
Понравилась статья?
Подпишитесь на наш блог и получайте наши статьи первым!
Или подписывайтесь на нас в соцсетях:
Заметили ошибку? Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так


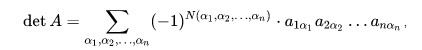
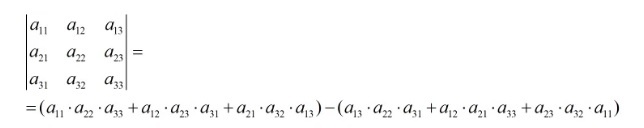
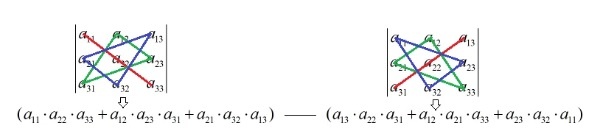
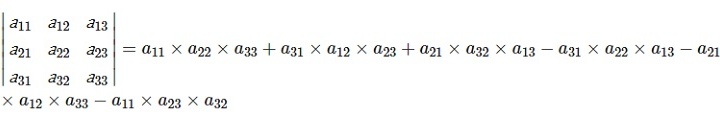
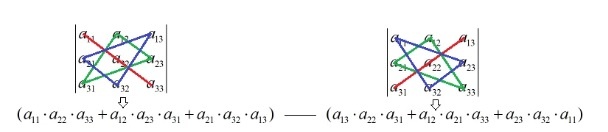
Бесплатно отвечаем на ваши вопросы. Задайте свой вопрос и получите ответ от профессионального преподавателя. Выберите лучший ответ.
Вопросы могут задавать только авторизованные пользователи. Войти