Задачи на нахождение напряженности электрического поля, как правильно решать

С электрическим полем человек сталкивается не только на уроках физики в школе или институте, но и в повседневной жизни. Изучение такого явления способствует техническому прогрессу. Важно уметь пользоваться основными формулами для расчета характеристик электрического поля, что поможет понять природу взаимодействия заряженных тел и решать задачи любой сложности.

Электрическое поле: решение задач

Электромагнитное поле возникает в процессе изменений магнитного поля, к примеру, в волнах электромагнитного характера. В физике можно встретить множество задач по теме электрического поля. Для того чтобы рассчитать характеристики данного явления, необходимо знать фундаментальные законы и основные формулы.

Электрическое поле выступает в роли материального передатчика взаимодействия заряженных частиц, который формируется вокруг наэлектризованных тел. Свойства такого физического явления:

• образуется зарядами;
• воздействует на заряженные частицы.

Напряженностью электрического поля является векторная величина в виде силовой характеристики электрического поля. Данный параметр определяется отношением силы воздействия поля на точечный положительный заряд и этого заряда. Обозначается напряженность таким образом: \(\vec{E}\) (Н/Кл)

Формула для расчета напряженности электрического поля выглядит следующим образом:

\(\vec{E}=\frac{\vec{F}}{q}\)

где q является зарядом, на который действует поле.

Напряженность поля точечного заряда определяется, согласно формулам:

\(E=\frac{F}{q}\)

\(F=K\frac{\left|Q \right|\times \left|q \right|}{r^{2}\times \varepsilon }\)

Таким образом:

\(E=K\frac{Q}{r^{2}\times \varepsilon }\)

Можно сделать вывод, что поле уменьшается при увеличении расстояния.

Принцип суперпозиции полей заключается в том, что при нахождении в точке пространства различных заряженных частиц, создающих электрические поля с напряженностью:

\(\vec{E_{1}}\), \(\vec{E_{2}}\), \(\vec{E_{3}}\), \(\vec{E_{n}}\)

Результирующая напряженности поля в указанной точке будет равна геометрической сумме этих напряженностей:

\(\vec{E}=\vec{E_{1}}+\vec{E_{2}}+\vec{E_{3}}...+\vec{E_{n}}\)

Задача №1. Закон Кулона

Шар, обладающий зарядом, соприкасается с аналогичным незаряженным шаром. Если расстояние между этими объектами составляет r=15 см, то они отталкивают друг друга с силой F=1 мН. Требуется рассчитать первоначальный заряд заряженного шара.

Решение

Соприкасаясь, одинаковые объекты делят пополам первоначальный заряд. С помощью данной силы взаимодействия можно рассчитать заряды шаров, которыми они стали обладать после соприкосновения. Перед этим необходимо перевести все величины в единицы СИ:

\(F=10^{-3}\) H

\(r = 0,15\) м

Затем необходимо записать основные формулы:

\(F=\frac{kq^{2}}{r^{2}}\)

\(q^{2}=\frac{Fr^{2}}{k}\)

\(k=\frac{1}{4\pi \varepsilon _{0}}=9\times 10^{9}\)

Подставив значения, получим уравнение:

\(q=\sqrt{\frac{Fr^{2}}{k}}=\sqrt{\frac{10^{-3}\times (0.15)^{2}}{9\times 10^{9}}}=5\times 10^{-8}\)

Известно, что первоначальный заряд был в два раза больше:

\(q=2\times 5\times 10^{-8}=10^{-7}\)

Ответ: первоначальный заряд составлял \(10^{-7}\) Кл или 10 мкКл.

Задача №2. Электрическое поле

Необходимо определить силу взаимодействия двух заряженных частиц, которые обладают зарядами по 10 нКл и удалены друг от друга на 3 см. Данные заряды можно считать точечными и находящимися в вакуумной среде.

Решение

Требуется записать значение величин в стандартном виде:

\(q_{1}=q_{2}=10\) нКл или \(10^{-8}\) Кл

\(r=3\) см или  \(r=3*10^{-2}\) м

Далее необходимо записать формулу для F:

\(F=k\frac{\left|q_{1} \right|\times \left|q_{2} \right|}{r^{2}}\)

Подставив числовые значения, получим:

\(F=9\times 10^{-9}\frac{10^{-8}\times 10^{-8}}{\left(3\times 10^{-2} \right)^{2}}=10^{-3}\) Н или 1 мН

Ответ: заряды взаимодействуют с силой в 1мН.

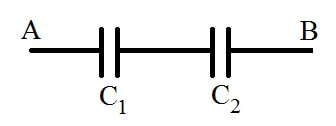
Задача №3. Конденсатор

Разность потенциалов между точками А и В составляет U=9 В. Значения емкости конденсаторов равны соответственно \(C_{1}=3\) мкФ и \(C_{2}=6\) мкФ. Требуется определить заряды \(Q_{1}\) и \(Q_{2}\) и разности потенциалов \(U_{1}\) и \(U_{2}\) для обкладок первого и второго конденсаторов.

Решение

Общая емкость такого соединения составит:

\(\frac{1}{C_{\Sigma }}=\frac{1}{C_{1}}+\frac{1}{C_{2}}\)

\(C_{\Sigma }=\frac{C_{1}\times C_{2}}{C_{1}+C_{2}}=\frac{3\times 6}{3+6}=2\) мкФ

Емкость рассчитана в микрофарадах для того, чтобы не прибегать к расписыванию степени десятки.

Величину заряда можно определить по формуле:

\(q_{\Sigma }=C_{\Sigma }\times U=2\times 9=18\) мкКл

Если соединение пластин конденсатора выполнено последовательно, то заряды будут обладать одинаковыми значениями. Таким образом, можно записать справедливые равенства:

\(q_{1}=q_{\Sigma }=C_{1}\times U_{1}\)

\(q_{2}=q_{\Sigma }=C_{2}\times U_{2}\)

Формула для определения напряжения на конденсаторах будет записана таким образом:

\(U_{1}=\frac{q_{1}}{C_{1}}=\frac{18\times 10^{-6}}{3\times 10^{-6}}=6\) В

\(U_{2}=\frac{q_{2}}{C_{2}}=\frac{18\times 10^{-6}}{6\times 10^{-6}}=3\) В

Ответ: разность потенциалов составляет 18 мкКл, напряжения соответственно равны 6 В и 3В.

Задача №4. Энергия конденсатора

Диэлектрическая проницаемость диэлектрика, которым заполнили плоский конденсатор, равна 2. Если конденсатор не имеет диэлектрика, то его энергия составляет 20 мкДж. Требуется рассчитать энергию конденсатора, отключенного от питания и заполненного диэлектрическим веществом.

Решение

Энергию конденсатора в незаполненном состоянии можно рассчитать по формуле:

\(W_{0}=\frac{q_{0}}{2C_{0}}=\frac{C_{0}U_{0}^{2}}{2}\)

Когда конденсатор заполнили диэлектриком, его емкость изменится таким образом:

\(C_{1}=\varepsilon C_{0}\)

Исходя из этого утверждения, энергию конденсатора можно определить так:

\(W_{1}=\frac{\varepsilon C_{0}U_{0}^{2}}{2}=\varepsilon W_{0}=2\times 20=40\) мкФ

Ответ: энергия конденсатора после заполнения диэлектрика составит 40 мкФ.

Задача №5. Потенциал поля

Два точечных зарядов величиной 100 нКл и 10 нКл удалены друг от друга на расстояние r = 10 см. Требуется определить потенциальную энергию системы этих зарядов.

Решение

Формула для расчета точечного заряда имеет вид:

\(\phi =\frac{q}{4\pi \varepsilon _{0}r}\)

Таким образом, потенциальную энергию зарядов можно рассчитать по формуле:

\(E=\frac{q_{1}q_{2}}{4\pi \varepsilon _{0}r}\)

Подставив числовые значения, получим:

\(E=\frac{10^{-7}\times 10^{-8}}{4\pi \times 8.85\times 10^{-12}\times 0.1}=9\times 10^{-5}\) Дж

Ответ: потенциальная энергия системы зарядов равна \(9\times 10^{-5}\) Дж

Вопросы на тему «Электрическое поле»

1. Как переводится слово electron с греческого языка? Ответ: Янтарь.
2. Название величины, которая характеризует свойство объектов участвовать в электромагнитных взаимодействиях. Ответ: Электрический заряд.
3. Каким образом обозначают электрический заряд в физике. Ответ: с помощью букв q или Q.
4. Единица заряда в международной системе СИ. Ответ: кулон.
5. Прибор для определения заряженных частиц. Ответ: электрометр.
6. Что такое точечный заряд? Ответ: точечным зарядом является заряженное тело с размерами, которые существенно меньше, чем расстояние между этим телом, точкой наблюдения или другими заряженными телами.
7. Пример положительно заряженных тел. Ответ: стекло, наэлектризованное путем трения о шелковую ткань.
8. Пример отрицательно заряженных тел. Ответ: эбонитовая палочка, наэлектризованная путем трения о шерстяную ткань.
9. Описать взаимодействие заряженных тел. Ответ: одинаковые заряды отталкиваются, а разноименные – притягиваются.
10. Объяснить понятие дискретности электрического заряда. Ответ: Дискретность заряда означает существование некоторого наименьшего, универсального, далее не делимого элементарного заряда.
11. Какова величина элементарного заряда? Ответ: \(e=1,6\times 10^{-19}\) Кл.
12. Дать определение протона и электрона. Ответ: Частицу, которая обладает элементарным положительным зарядом, называется протоном. Частица, для которой характерен элементарный отрицательный заряд, является электроном.
13. Объяснить положительный и отрицательный заряд тела. Ответ: Тело будет заряжено положительно, если в нем преобладает количество протонов по сравнению с числом электронов. При избытке электронов тело будет заряжено отрицательно.
14. Закон сохранения электрического заряда. Ответ: в условиях замкнутой системы алгебраическая сумма электрических зарядов сохраняет постоянное значение при любых взаимодействиях внутри этой системы.
15. Что такое изолированная или замкнутая система? Ответ: изолированной или замкнутой системой тел является такая система, в которую не добавляют и не выводят из нее электрические заряды.
16. Способы электризации тел. Ответ: трением, воздействием различных излучений, с помощью электрической индукции.
17. Когда открыт закон Кулона? Ответ: в 1785 году.
18. Какой прибор Кулон использовал в опытах? Ответ: крутильные весы.
19. Запись закона Кулона. Ответ: \(F=k\frac{\left|q_{1} \right|\times \left|q_{2} \right|}{r^{2}}\)
20. Что называют точечным зарядом? Ответ: точечным зарядом называют заряженное тело с размерами, которые можно не учитывать в решении данной задачи.
21. Единица заряда. Ответ: кулон (кл).
22. Представить запись электрической постоянной. Ответ: \(\varepsilon _{0}=8,85\times 10^{-12}\) Кл2/Н*м2.
23. Назвать источник и ключевое свойство электрического поля. Ответ: электрическое поле создается любым заряженным телом, его главным свойством является действие на электрические заряды с какой-то силой.
24. Определение напряженности. Ответ: напряженностью называют силовую характеристику электрического поля.
25. Что такое электростатическое поле. Ответ это электрическое поле зарядов, которые не двигаются и не меняются в течение времени.
26. Зачем нужны силовые линии? Ответ: с помощью силовых линий наглядно представляют электрическое поле.
27. Чему равна работа сил электростатического поля, если заряд перемещается по какой-то замкнутой траектории. Ответ: нулю.
28. Дать определение потенциала электрического поля. Ответ: физическая величина, которая равна отношению потенциальной энергии электрического заряда в электрическом поле к величине этого заряда.
29. Единицы измерения потенциала в СИ. Ответ: вольт.

Зная методику решения распространенных задач по теме электрического поля, можно без труда выполнять расчеты основных его показателей. Такие навыки и умения пригодятся для более углубленного изучения электромагнетизма и сопутствующих тем. При возникновении каких-либо трудностей в процессе освоения материала можно обратиться за помощью к ресурсу Фенинкс.Хелп.