Уравнение Шредингера в квантовой физике
Уравнение Шредингера имеет большое значение для квантовой механики — наряду со вторым законом Ньютона в классической механике или уравнением Максвелла для изучения природы электромагнитных волн. Закономерности, описанные ученым, объясняют движение частиц, скорость которых существенно меньше, чем скорость света.
Общее уравнение Шредингера — какой имеет вид и зачем нужно
Уравнением Шредингера называют линейное дифференциальное равенство с частными производными, которое описывает изменение в пространстве и во времени чистого состояния посредством волновой функции в гамильтоновых квантовых системах.
Опытным путем можно наблюдать волновые свойства частиц. Определение данного явления является следствием уравнения, которое описывает движение микроскопических частиц в разных силовых полях. Закономерности движения в квантовой механике вытекают из статистического толкования волн де Бройля и соотношения неопределенностей Гейзенберга.
Главное уравнение представляет собой формулу относительно волновой функции \(\psi\) (x, y, z,t). Это объясняется тем, что \(\left|\psi \right|\) является определением вероятности присутствия частицы в определенное время t в объеме ΔV, то есть в области со следующими координатами:
x и x + dx;
y и y + dy;
z и z+dz.
Основная закономерность нерелятивистской квантовой механики была представлена в 1926 году Э. Шредингером. Данная формула не является выводом, это — постулат. Справедливость уравнения подтверждается согласием с результатами опыта, что говорит о природном характере выявленной закономерности.
Общее уравнение Шредингера обладает следующим видом:
\(-\frac{h^{2}}{2m}\Delta \psi +U\psi =i\times h\frac{d\psi }{dt}\)
где ħ равно отношению \(\frac{h}{2\pi }\)
m — является массой частицы,
Δ — оператор Лампаса,
i — представляет собой мнимую единицу,
U(x, y, z, t) — равно потенциальной функции частицы в силовом поле, в котором она движется,
\(\psi\)(x, y, z, t) — служит искомой волновой функцией частицы.
Данная формула справедлива для любых частиц, спин которых равен нулю, движущихся с небольшой скоростью относительно скорости света. Уравнение можно дополнить условиями, характерными для волновой функции:
- волновая функция имеет конец, однозначна и непрерывна;
- производные волновой функции отличаются непрерывностью;
- \(\left|\psi \right|\) интегрируема, что является условием нормировки вероятностей.
В первом случае описано уравнение, которое зависит от времени. Многие физические явления, наблюдаемые в микромире, можно охарактеризовать с помощью упрощенной формулы. При исключении зависимости волновой функции от времени можно определить закономерность Шредингера для стационарных состояний, то есть состояний, в которых значения энергии фиксированы. Такие ситуации возможны при стационарном силовом поле, в котором происходит движение частицы. Таким образом, функция U = U (x, y, z) не определяется временем и обладает смыслом потенциальной энергии.
В данном случае уравнение Шредингера будет иметь следующий вид:
\(\Delta \psi +\frac{2m}{h^{2}}\left(E-U \right)\times \psi =0\)
Данная формула получила название уравнения Шредингера для стационарных состояний. Здесь используют полную энергию Е-частицы. Согласно теории дифференциальных уравнений доказано, что имеется бесчисленное множество решений подобных уравнений, которые имеют физический смысл при отборе методом наложения граничных условий. В случае уравнения Шредингера такими условиями являются характеристики регулярности волновых функций:
- конечность волновых функций;
- однозначность и непрерывность волновых функций наряду с первыми производными.
Реальным физическим смыслом обладают лишь те решения, которые определены регулярными функциями $$\left|\psi \right|$$. Регулярные решения характерны не для любых значений величины Е, а лишь при конкретной их совокупности в рамках определенной задачи. Такие параметры энергии носят название собственные. В свою очередь решения с собственными значениями энергии определяют как собственные функции. С помощью собственных параметров Е формируют непрерывный или дискретный ряд. Для первого случая характерен непрерывный или сплошной спектр, для второго — дискретный спектр.
Применение уравнения Шредингера
Уравнение Шредингера не подходит для описания следующих явлений:
- Спонтанное излучение, в связи с тем, что волновая функция для возбужденного состояния представляет собой точное решение уравнения Шредингера с учетом зависимости от времени.
- Процесс изменения, характерный для квантовой механики, так как уравнение линейно, детерминистично и обладает обратимостью во времени, а данный процесс не отличается линейностью, стохастичен и необратим.
- Взаимное превращение элементарных частиц, по причине описания данных процессов релятивистской квантовой теорией поля.
Можно рассмотреть применение уравнения Шредингера к свободной частице или электрону, который совершает движение вдоль оси ОХ. При этом величина потенциальной энергии частицы, находящейся в свободном движении, равна нулю. То есть U = 0. Тогда уравнение Шредингера будет иметь следующий вид:
\(\Delta \psi +\frac{2m}{h^{2}}E\psi =0\)
Исходя из гипотезы Бройля, можно смоделировать перемещение такого микроскопического объекта с помощью плоской монохроматической волны, занимающей все пространство:
\(\psi =\psi _{0}e^{-i\left(\omega t-\vec{k}\vec{y} \right)}\)
Волновая функция, характеризующая движение свободной частицы вдоль оси ОХ, бедт записана следующим образом:
\(\psi =\psi _{0}e^{-i\left(\omega t-kx \right)}\)
где \(\psi _{0}\) является амплитудой волны.
Круговая частота \(\omega\) и волновое число k связаны с полной энергией E и импульсом р следующими закономерностями:
\(E=hω\)
\(p=hk\)
Из данных соотношений следует:
\(\omega = \frac{E}{h}\)
\(k=\frac{P}{h}\)
В таком случае волновая функция будет иметь следующий вид:
\(\psi =\psi _{0}e^{\frac{i}{h}\left(Et-Px \right)}\)
Продемонстрировать соответствие данного вида функции уравнению Шредингера можно, если определить \(\Delta \psi\) и \(P^{2}\)
\(\frac{d\psi }{dx}=\psi _{0}\left(\frac{-i}{h} \right)\left(-P \right)\times e^{\frac{-i}{h}\left(Et-Px \right)}=\frac{i}{h}P\psi\)
\(\Delta \psi =\frac{d^{2}\psi }{dx^{2}}=\left(\frac{i}{h}P \right)^{2}e^{-\frac{i}{h}\left(Et-Px \right)}\psi _{0}=-\frac{P^{2}}{h^{2}}\psi\)
\(P^{2}=\frac{1}{\psi }h^{2}\Delta \psi\)
Далее необходимо определить \(\frac{d\psi }{dt}\) и определить значение полной энергии Е:
\(\frac{d\psi }{dt}=-\psi _{0}\frac{i}{h}E\times e^{-\frac{i}{h}\left(Et-Px \right)}=-\frac{i}{h}E\psi\)
\(E=-\frac{1}{\psi }\times \frac{h}{i}\times \frac{d\psi }{dt}\)
Используя отношение энергии частицы Е к импульсу p, получим формулу:
\(E=\frac{p^{2}}{2m}\)
Подставив данные значения в уравнение, можно вывести следующее равенство:
\(-\frac{1}{\psi }\times \frac{h}{i}\frac{d\psi }{dt}=\frac{1}{2m}\left(-\frac{1}{\psi }h^{2}\Delta \psi \right)\)
\(\frac{h}{i}\frac{d\psi }{dt}=\frac{h^{2}}{2m}\Delta \psi\)
\(\frac{h^{2}}{2m}\Delta \psi =ih\frac{d\psi }{dt}\)
\(-\frac{h^{2}}{2m}\Delta \psi =ih\frac{d\psi }{dt}=ih\left(-\psi _{0} \right)\frac{i}{h} Ee^{-\frac{i}{h}\left(Et-Px \right)}=E\psi\)
\(\Delta \psi +\frac{2m}{h^{2}}E\psi =0\)
Данное равенство соответствует уравнению Шредингера, когда U=0. Корректный вид волновой функции можно обосновать для случая движения частицы в силовом поле, в случае, когда потенциальная энергия не равна нулю. Формула будет иметь следующий вид:
\(\frac{P^{2}}{2m}= E-U\)
Такое уравнение характеризует энергию движения частицы по аналогии с кинетической энергией в классической механике. После подстановки значений Е и Р уравнение приобретает следующий вид:
\(\frac{1}{2m}\left(-\frac{1}{\psi }h^{2}\Delta \psi \right)=-\frac{1}{\psi }\frac{h}{i} \frac{d\psi }{dt}-U\)
\(-\frac{h^{2}}{2m}\Delta \psi +U\psi =\frac{h}{i}\frac{d\psi }{dt}\)
Конечная формулировка идентична уравнению Шредингера. Данное выражение применимо для частицы, которая совершает движение в силовом поле.
Пример решения уравнения Шредингера
Задание 1
Электрон движется в одном измерении вдоль оси ОХ между двумя потенциальными барьерами. В случае, если высота барьеров на концах ямы не имеет ограничений, электрон, как и в атоме, совершает финитное движение. Необходимо описать движение в квантовой механике и поведение импульса и энергии частицы.
Решение
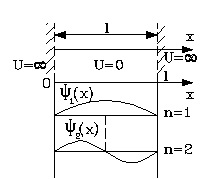
Вначале следует изобразить ситуацию схематично
Согласно условиям задачи, функция U(x) обладает особым, разрывным видом и равна нулю в области между стенками. На краях ямы, то есть на ее барьерах, функция будет бесконечна:
При х=0 и х=l \(U=\propto\)
При 0<x<1 U=0
Можно представить импульс электрона по модулю в виде определенной и постоянной величины, изменяющей знак во время отражения от барьера. Связь энергии электрона и импульса выражается таким образом:
\(E=\frac{p^{2}}{2m_{0}}\)
Уравнение Шредингера для стационарных состояний частиц, находящихся между барьерами, имеет следующий вид:
\(\frac{h^{2}}{2m_{0}}\times \psi ^{"}+E\psi =0\)
Выполняя преобразования в формулах, получим:
\(\psi ^{"}+\frac{p^{2}}{h^{2}}\psi =0\)
К полученной формуле следует прибавить граничные условия на барьерах ямы. Необходимо учесть связь волновой функции и вероятности нахождения частиц. Согласно условиям задания, частица за пределами стенок не находится. В таком случае значение волновой функции на стенках и за их пределами равно нулю. Граничные условия задания будут иметь следующий вид:
\(x\leq 0 \) \( \psi =0\)
\(x\leq 1 \) \( \psi =0\)
При дальнейших действиях нужно учитывать, что решением последней формулы являются волны де-Бройля. Одну волну де-Бройля в качестве решения к задаче не применить, так как с ее помощью заранее описывается свободная частица, движущаяся в одном направлении. В данном случае рассматривается движение частицы между стенками. Поэтому, используя принцип суперпозиции, в решении можно применить две волны де-Бройля, совершающих движение навстречу друг к другу с импульсами р и –р. Формула будет иметь следующий вид:
\(\psi =C_{1}\times exp\left(\frac{i}{h}px \right)+C_{2}\times exp\left(-\frac{i}{h}px \right)\)
Исходя из граничных условий и условий нормировки, можно определить постоянные \(С_1\) и \(С_2\). Сумма всех вероятностей позволит рассчитать вероятность нахождения электрона между стенками в любом месте и получить единицу, то есть значение вероятности достоверного события равна 1. Уравнение будет иметь такой вид:
\(\int_{0}^{l}{\left|\psi \left(x \right) \right|^{2}}dx=1\)
Исходя из первых граничных условий:
\(C_{1}+C_{2}=C\)
\(C_{1}=-C_{2}=C\)
Решение задачи будет иметь следующий вид:
\(\psi =C\times \left(exp\left(\frac{i}{h}px \right)-exp\left(-\frac{i}{h}px \right) \right)\)
\(exp\left(\frac{i}{h}px \right)-exp\left(-\frac{i}{h}px \right) =2\sin \frac{px}{h}\)
\(\psi =A\sin \frac{px}{h}\)
\(A=2iC\)
Постоянная А выходит из условий нормировки. В данном случае она не представляет интереса. Необходимо использовать второе граничное условие. Тогда решение можно записать в виде уравнения:
\(\sin \frac{pl}{h}=0\)
Импульс при этом принимает только определенные значения:
\(p_{n}=\frac{h}{l}\pi n\)
n=±1, ±2…
Следует учесть, что n не равно нулю. Это объясняется тем, что в противном случае волновая функция повсюду имела нулевые значения. В этом случае для частицы между стенками состояние покоя не характерно. Электрон обязательно должен совершать движение. Минимальное значение возможного импульса движущейся частицы равен:
\(\frac{h}{l}\pi =\frac{hn}{2\pi }\frac{\pi }{l}=\frac{hn}{2l}\)
Ранее было указано, что импульс электрона изменяет знак во время отражения от барьеров. В этом заключается сложность представления ответа на вопрос, каков импульс у частицы, запертой между стенками. Он может быть равен –р или +р. Импульс не определен. Степень неопределенности будет выражаться в следующем:
рх-(-р)=2р
Неопределенность координаты Δх равна l. Обнаружить частицу можно в пределах между барьерами. Точное местонахождение электрона неизвестно. Наименьшее значение импульса имеет вид:
\(\frac{h}{2l}\)
Исходя из этого условия, можно вывести равенство:
\(\Delta x\times \Delta p_{x}=h\)
Таким образом, соотношение Гейзенберга в рамках данной задачи, то есть при наличии наименьшего значения р, подтверждено. В случае произвольно-возможного значения импульса соотношение неопределенности приобретает такой вид:
\(\Delta x\times \Delta p_{x}\geq h\)
Согласно исходному постулату Гейзенберга-Бора о неопределенности Δх и Δу, установлена лишь нижняя граница неопределенностей, возможная при измерениях. В начале движения наблюдают минимальные неопределенности, которые возрастают со временем. Полученное уравнение демонстрирует следующее: импульс системы в квантовой механике не всегда изменяется непрерывно. Спектр импульса электрона в данном случае дискретный, импульс частицы между барьерами изменяется скачкообразно. Величина такого скачка при условиях задания является постоянной величиной и определяется как:
\(\frac{h}{2l}\)
Можно изобразить спектр возможных значений импульса электрона. Дискретность изменения механических величин, не применимая к классической механике, в квантовой механике является следствием ее математического аппарата. Невозможно представить наглядное объяснение скачкообразного изменения импульса. Это закон квантовой механики, данный вывод следует из него логически и является объяснением.
Далее необходимо обратиться к энергии электрона. Данная величина обладает связью с импульсом. В случае дискретного спектра импульса получают дискретный спектр значений энергии частицы между барьерами. Подставив ранее известные формулы в уравнение, получим:
\(E_{n}=\frac{p_{n}^{2}}{2m_{0}}=\frac{1}{2m_{0}}\times \left(\frac{h}{2l} \right)^{2}n^{2}\)
где n = 1, 2,…, представляет собой квантовое число.
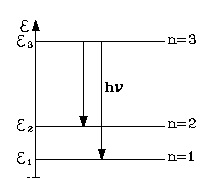
Таким образом, получают энергетические уровни.
На рисунке представлены энергетические уровни, согласно условию задания. Если изменить их, то схема расположения энергетических уровней будет изменена. В случае, когда частица обладает зарядом, как электрон, и расположена на самом низком энергетическом уровне, она будет в состоянии спонтанно испускать свет, как фотон. При этом переход на более низкий энергетический уровень возможен с условием:
\(E_{n}-E_{M}=h\times \nu _{nm}\)
Для этого задания волновые функции, характерные каждому стационарному состоянию, являются синусоидами. Их нулевые значения будут отмечены на стенках.
Уравнение Шредингера имеет огромное значение для развития современной науки. Квантовая механика является популярной дисциплиной для изучения в специализированных вузах. Нередко студенты учебных заведений сталкиваются со сложными задачами, решение которых отыскать порой достаточно сложно.
При возникновении трудностей в образовательном процессе получить квалифицированную помощь можно с помощью сервиса Феникс.Хелп.
Понравилась статья?
Подпишитесь на наш блог и получайте наши статьи первым!
Или подписывайтесь на нас в соцсетях:
Заметили ошибку? Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так


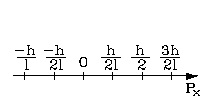
Бесплатно отвечаем на ваши вопросы. Задайте свой вопрос и получите ответ от профессионального преподавателя. Выберите лучший ответ.
Вопросы могут задавать только авторизованные пользователи. Войти