Как решать интегралы: примеры решения

Одно из самых значимых понятий в математике — интеграл. Термин часто можно встретить при решении задач по математике и физике. С помощью интеграла существенно упрощается поиск площади под кривой, пройденного пути объекта, движущегося неравномерно, массы неоднородного тела, функции по производной.

Что такое интеграл — понятие и определение

Интеграл является эффективным инструментом для решения задач из математического анализа. Слово «интеграл» происходит от латинского «integer», то есть «целый». Впервые это понятие ввел Иоганн Бернулли.

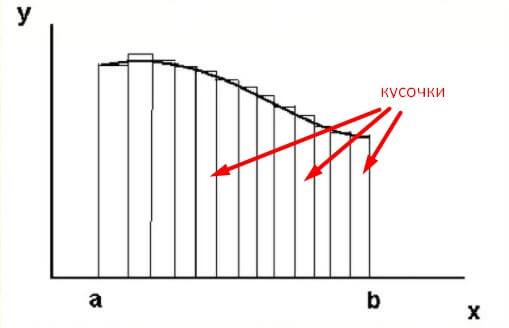
Разобраться в определении интеграла можно, если рассмотреть понятный график функции:

Исходя из графика, можно сделать вывод, что интегралом является сумма малых частей, которые составляют в целом рассматриваемый объект. Компоненты складываются в какую-то геометрическую фигуру. При сложении этих частей можно определить, какова ее площадь. Таким образом, пояснение для интеграла заключается в следующем: интеграл является площадью какой-то фигуры, расположенной под линией функции.

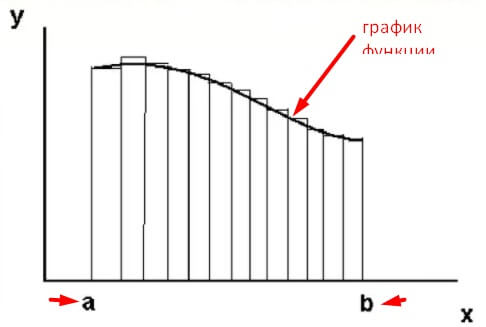
Данное понятие относится к определенному интегралу. Он определен на отрезке между точками а и b. В верхней части в качестве ограничения выступает некоторый график функции, как представлено на рисунке:

Математическая запись интеграла:

\(\int_{a}^{b}{f(x)dx}\)

где f(x) является той самой функцией, график которой ограничивает фигуру в верхней части;

a и b представляют собой пределы;

x соответствует направлению, вдоль которого построены столбцы на графике.

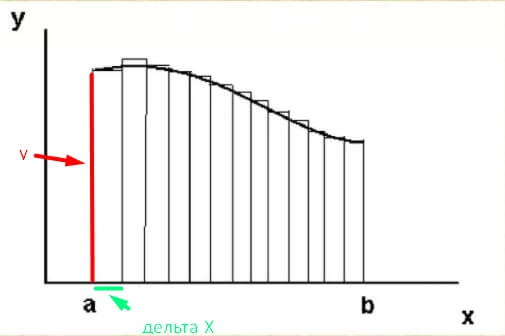
Процесс интегрирования является обратным дифференцированию. В том случае, когда требуется определить минимальный промежуток заданной функции, целесообразно взять от нее производную. Это объясняется тем, что производная или дифференциал являются быстрым методом поиска части чего-либо. Можно наглядно определить с помощью рисунка, что минимальная фигура, которая является частью целого, при таком числе составляющих компонентов не повторяет форму кривой функции. Таким образом, требуется уменьшить габариты таких частей, чтобы они максимально точно совпадали с графиком. Площадь наименьшего компонента фигуры будет стремиться к нулевому значению. Точность повышается с уменьшением размеров рассматриваемой части. Площадь геометрической фигуры состоит из суммы таких частей, которые стремятся к нулю. Записать это можно с помощью уравнения:

\(P=\lim_{\Delta x_{i}\rightarrow 0}\sum{y_{i}\Delta x_{i}}\)

Подробно полученное выражение можно рассмотреть на графике:

Площадь малой части фигуры определяется так же, как площадь прямоугольника. Значение Y нужно помножить на значение ΔХ. Так как фигура представляет собой совокупность малых частей, то их требуется сложить. Следует учитывать, что каждый компонент фигуры ΔХ стремится к нулевому значению. Поэтому формула, которая представлена выше, включает это условие и позволяет определить результат максимально точно.

Если обозначить количество частей ΔХ, стремящихся к бесконечности, то можно определить, что существует предел интегральной суммы, которая состоит из таких компонентов, стремящихся к нулю и к бесконечности по числу таких частей. Таким образом, правая граница фигуры, изображенной на графике, является пределом. В этом выражается геометрический смысл определенного интеграла.

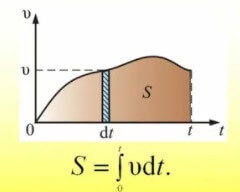
Физический смысл интеграла состоит в том, что это сумма бесконечно малых величин на бесконечно большом интервале. Исходя из этого, можно определить любую величину, которая изменяется, согласно функции. К примеру, рассчитать общий путь по закону изменения скорости. Необходимость в интеграле возникла, когда потребовалось рассчитать площади каких-либо фигур и объем любых тел, выбранных произвольно.

В том случае, когда расчеты подразумевают наличие постоянной характеристики, к примеру, скорости, найти путь можно с помощью произведения этой постоянной скорости и времени. Этот же момент можно проверить при вычислении интеграла от такой функции и записи уравнения прямой. Но скорость в процессе движения может меняться. Данное изменение можно представить в виде зависимости. Тогда следует вписать граничные условия, например, в случае пути — это время, в интеграл скорости по времени. Полученное выражение будет равно площади трапеции, которая расположена под функцией скорости, что является физическим смыслом определенного интеграла.

Свойства, которыми обладает определенный интеграл:

1. Когда функции f и g интегрируются на интервале [a, b], то для любых чисел \(\alpha\) и \(\beta (\alpha \in R,\ \beta \in R)\) функция \(\varphi(x) = \alpha f(x) + \beta g(x)\) также интегрируема на отрезке [a, b]. Справедливо равенство: \(\int\limits_a^b (\alpha f(x) + \beta g(x)) dx = \alpha \int\limits_a^b f(x) dx + \beta \int\limits_a^b g(x) dx.\label{ref1}\)
2. Если функции f и g интегрируемы на отрезке [a, b], то функция \(\varphi(x) = f(x)g(x)\) также интегрируема на этом отрезке.
3. В том случае, когда функция f(x) интегрируема на отрезке \(\Delta = [a, b]\) она интегрируема на любом отрезке \(\Delta_{1} \subset \Delta.\)
4. При функции f(x), интегрируемой на отрезке [a, b] и a < c  < b, будет работать формула: \(\int\limits_a^b f(x) dx = \int\limits_a^c f(x) dx + \int\limits_c^b f(x) dx\)
5. При функции f, интегрируемой на отрезке [a, b] и если \(c_{1}, c_{2}, c_{3}\) являются любыми точками данного интервала, то \(\int\limits_{c_{1}}^{c_{3}} f(x) dx = \int\limits_{c_{1}}^{c_{2}} f(x) dx + \int\limits_{c_{2}}^{c_{3}} f(x) dx\)

Термин «неопределенный интеграл» применим в ситуациях, когда требует найти площадь криволинейной трапеции, путь в соответствии с известной скоростью тела, которое движется неравномерно, и для решения других подобных задач.

Свойства, которыми характеризуется неопределенный интеграл:

1. Константу можно выносить за знак интеграла: \(\int kf(x) dx = k\int f(x) dx\)
2. Интеграл разности или суммы функций соответствует разности или сумме интегралов от этих функций: \(\int ( f(x) \pm g(x) ) dx = \int f(x) dx \pm \int g(x) dx\)
3. Производная интеграла определяется как выражение, находящееся под знаком интеграла: \(\bigg (\int f(x) dx \bigg )' = f(x)\)
4. Интеграл от производной функции равен сумме этой функции и постоянной: \(\int F'(x) dx = F(x) + C\)
5. Интеграл дифференциала функции равен сумме этой функции и постоянной интегрирования: \(\int df(x) dx = f(x) + C\)

Таблица интегралов для студентов

Такие формулы позволяют упростить решение многих задач. Основные интегралы:

\(\int 0dx=C\)

\(\int dx=\int 1dx=x+C\)

\(\int x^n dx = \frac{x^{n+1}}{n+1}+C\)

\(\int \frac{dx}{x}=\ln |x|+C\)

\(\int a^x dx = \frac{a^x}{\ln a} + C\)

\(int e^x dx = e^x + C\)

\(\int \sin x dx = -\cos x + C\)

\(\int \cos x dx = \sin x+C\)

\(\int \frac{dx}{\sin^2 x}=-ctgx + C\)

\(\int \frac{dx}{\cos^2 x}=tgx+C\)

\(\int \frac{dx}{\sqrt{a^2-x^2}}=\arcsin \frac{x}{a}+C\)

\(\int \frac{dx}{a^2+x^2}=\frac{1}{a}arctg\frac{x}{a}+C\)

\(\int \frac{dx}{a^2-x^2}=\frac{1}{2a} \ln|\frac{a+x}{a-x}|+C\)

\(\int \frac{dx}{\sqrt{x^2\pm a^2}}=\ln|x+\sqrt{x^2\pm a^2}|\)

Методы решения интегралов

Данные методики позволяют преобразовать сложные уравнения в простые формы, решения которых можно найти в таблице. Также к преобразованным выражениям можно применять свойства интегралов.

Непосредственное интегрирование

Данный метод целесообразно применять, когда в интеграле имеются табличные простейшие функции, либо функции, которые можно представит в таком виде по результатам элементарных действий. К примеру, когда требуется вынести константу за знак интеграла, разбить интеграл на слагаемые в виде интегралов, чтобы в подынтегральном выражении присутствовала готовая функция для интегрирования. Можно привести простой пример:

Необходимо определить интеграл непосредственным интегрированием:

\(\int \bigg ( x^3 + \frac{3}{2\sqrt{x}} + \frac{2}{x} \bigg ) dx\)

Исходя из свойства суммы интегралов, получим:

\(\int \bigg ( x^3 + \frac{3}{2\sqrt{x}} + \frac{2}{x} \bigg ) dx = \int x^3 dx + \int \frac{3 dx}{2\sqrt{x}} + \int \frac{2 dx}{x}\)

Первый интеграл записан в табличном виде. В таком случае можно воспользоваться непосредственным интегрированием:

\(\int x^3 dx = \frac{x^{3+1}}{3+1} = \frac{x^4}{4} + C\)

Второй интеграл обладает константой, которую допустимо вынести за знак. Затем интеграл будет преобразован в табличную форму:

\(\int \frac{3dx}{2\sqrt{x}} = 3 \int \frac{dx}{2\sqrt{x}} = 3 \sqrt{x} + C\)

В третьем интеграле можно вынести константу. Далее необходимо воспользоваться методом непосредственного интегрирования:

\(\int \frac{2dx}{x} = 2\int \frac{dx}{x} = 2 \ln x + C\)

Полученные выражения необходимо представить в виде одной записи:

\(\int \bigg ( x^3 + \frac{3}{2\sqrt{x}} + \frac{2}{x} \bigg ) dx = \frac{x^4}{4} + 3\sqrt{x} + 2\ln x + C\)

Ответ: \(\int \bigg ( x^3 + \frac{3}{2\sqrt{x}} + \frac{2}{x} \bigg ) dx = \frac{x^4}{4} + 3\sqrt{x} + 2\ln x+ C\)

Метод подведения под знак дифференциала

Решить некоторые типы интегралов можно с помощью этого способа. Он заключается в вынесении под знак интеграла. Таким образом получается интеграл табличной формы. Формула имеет следующий вид:

\(f'(x) dx = d( f(x) )\)

В том случае, когда подынтегральная функция содержит произведение пары функций, одна из которых представляет собой дифференциал другой, нужно внести под знак дифференциала нужную функцию. Данное действие можно записать таким образом:

\(\int f(\varphi(x)) \varphi'(x) dx = \int f(\varphi(x)) d(\varphi(x))=\int f(u) du\)

\(u=\varphi(x)\)

Воспользоваться способом подведения основных функций можно при знании таблицы производных и интегрирования. Из них следуют следующие уравнения:

\(dx = d(x+c) \)

\(c=const\)

\(-\sin x dx=d(\cos x)\)

\(dx=\frac{1}{a} d(ax)\)

\(\cos x dx = d(\sin x)\)

\(xdx=\frac{1}{2} d(x^2+a) \)

\(\frac{dx}{x} = d(\ln x)\)

\(-\frac{dx}{x^2}= d(\frac{1}{x})\)

\(\frac{dx}{\cos^2 x} = d(tg x)\)

\(\int f(kx+b)dx = \frac{1}{k} \int f(kx+b)d(kx+b) = \frac{1}{k} F(kx+b) + C\)

В качестве примера можно решить задачу на нахождение интеграла, обладающего таким видом:

\(\int \sin x \cos x dx\)

В этом случае допустимо заносить под знак дифференциала любую из указанных функций. Целесообразно занести \(cos x\) из-за удобства смены знаков. Применяя формулы, получим:

\(\int \sin x \cos xdx = \int \sin x d(\sin x) = \frac{1}{2} \sin^2 x + C\)

Ответ: \(\int \sin x \cos x dx = \frac{1}{2} \sin^2 x + C\)

Метод интегрирования по частям

Данная методика применима, когда требуется решить интегралы от произведения двух простейших функций. Одна из них достаточно просто дифференцируется, а вторая — интегрируется. В данном случае справедлива методика для неопределенных и определенных интегралов. Неопределенный интеграл характеризуется уравнением:

\(\int udv = uv - \int vdu\)

Определенный интеграл соответствует формуле:

\(\int \limits_{a}^{b} udv = uv \bigg |_{a}^{b} - \int \limits_{a}^{b} vdu\)

В качестве примера можно определить интеграл:

\(\int xe^xdx\)

Заметим, что в состав подынтегральной функции входит пара функций. Одна из них путем дифференцирования преобразуется в единицу, а вторая достаточно просто интегрируется. Поэтому в данном случае справедлив метод интегрирования по частям. Можно предположить, что:

\(u = x \rightarrow du=dx\)

\(dv = e^x dx \rightarrow v=e^x\)

Далее необходимо подставить полученные значения в первую формулу интегрирования:

\(\int xe^x dx = xe^x - \int e^x dx = xe^x - e^x + C\)

Ответ: \(\int xe^x dx = xe^x - e^x + C\)

Метод замены переменной или метод подстановки

Этот способ нахождения интегралов применим в задачах, где одна функция — это производная второй функции. Допустим, что интеграл записан так:

\(\int f(x) dx\)

Можно заменить \(x=\phi(t)\). При этом функция \(\phi(t)\) является дифференцируемой, поэтому можно найти \(dx = \phi'(t) dt.\)

Далее следует подставить \(\begin{vmatrix} x = \phi(t) \\ dx = \phi'(t) dt \end{vmatrix}\) в интеграл. Таким образом:

\(\int f(x) dx = \int f(\phi(t)) \cdot \phi'(t) dt\)

Полученное выражение является формулой замены переменной в неопределенном интеграле.

При условиях задачи, которая содержит интеграл \(\int f(\phi(x)) \cdot \phi'(x) dx\), целесообразно заменить переменную на новую:

\(t = \phi(x)\)

\(dt = \phi'(t) dt\)

Таким образом, интеграл преобразуется в форму, которую легко рассчитать с помощью основных методов интегрирования:

\(\int f(\phi(x)) \cdot \phi'(x) dx = \int f(t)dt\)

Следует помнить, что по итогам расчетов требуется вернуть замененную переменную назад к x.

Например, можно рассмотреть задачу, по условиям которой необходимо вычислить неопределенный интеграл с помощью замены переменной:

\(\int e^{3x} dx\)

Замена переменной будет выполнена следующим образом:

\(t = 3x\)

\(dt = 3dx\)

Таким образом:

\(\int e^{3x} dx = \int e^t \frac{dt}{3} = \frac{1}{3} \int e^t dt =\frac{1}{3} e^t + C = \frac{1}{3} e^{3x} + C\)

Ответ: \(\int e^{3x} dx = \frac{1}{3} e^{3x} + C\)

Примеры решения

Задача 1

Требуется рассчитать определенный интеграл:

\(\int_0^1 \frac{x}{x^4+1} dx\)

Решение

Требуется заменить \(t = x^2\)

Таким образом, \(dt = 2xdx\)

Далее необходимо пересчитать пределы интегрирования для переменной t. Для этого нужно подставить 0 и 1 в замену \(t = x^2\)

В данной задаче они остались прежними. После манипуляций с подстановками получим:

\(\int_0^1 \frac{x}{x^4+1}dx = \int_0^1 \frac{1}{2} \frac{dt}{t^2+1}\)

Можно найти интеграл по таблице:

\(\int_0^1 \frac{1}{2} \frac{dt}{t^2+1}=\frac{1}{2} arctg t \bigg |_0^1\)

Используя формулу Ньютона-Лейбница, запишем решение:

\(\frac{1}{2} arctg t \bigg |_0^1 =\frac{1}{2} arctg 1 - \frac{1}{2} arctg 0 = \frac{1}{2} \cdot \frac{\pi}{4} = \frac{\pi}{8}\)

Ответ: \(\int_0^1 \frac{x}{x^4+1} dx = \frac{\pi}{8}\)

Задача 2

Необходимо решить определенный интеграл:

\(\int_0^\pi (x+5)\sin x dx\)

Решение

Можно заметить произведение двух функций, которое находится под интегралом. В этом случае целесообразно воспользоваться методом интегрирования по частям:

\(\int udv = uv - \int vdu\)

\(\int_0^\pi (x+5) \sin x dx = \begin{vmatrix} u = x+5 & du = dx \\ dv = \sin x dx & v = -\cos x \end{vmatrix}\)

Нужно подставить в уравнение интегрирования по частям рассчитанные данные из вертикальных скобок:

\(-(x+5)\cos x \bigg |_0^\pi&nbsp;+ \int_0^\pi&nbsp;\cos x dx\)

С помощью формулы Ньютона-Лейбница для вычисления определенного интеграла запишем ответ:

\(-(x+5)\cos x \bigg |_0^\pi + \int_0^\pi \cos x dx = -(\pi+5) \cdot (-1) + 5 + \sin x \bigg |_0^\pi = \pi + 10 + \sin \pi - \sin 0 = \pi + 10\)

Ответ:  \(\int_0^\pi (x+5)\sin x dx = \pi + 10\)

Задача 3

Требуется найти определенны интеграл, записанный в виде:

\(\int_0^2 (x^3 + 2x + 2) dx\)

Решение

Используя способ разложения интеграла на простейшие, после получения промежуточного результата необходимо интегрировать каждый интеграл индивидуально:

\(\int_0^2 (x^3+2x+2) dx = \int_0^2 x^3dx + 2\int_0^2 xdx + 2\int_0^2 dx\)

В случае первых двух интегралов целесообразно воспользоваться правилом:

\(x^p = \frac{x^{p+1}}{p+1}\)

Третий интеграл содержит константу. Таким образом:

\(\int_0^2 x^3dx + 2\int_0^2 xdx + 2\int_0^2 dx = \frac{x^4}{4} \bigg |_0^2 + 2 \frac{x^2}{2} \bigg |_0^2 + 2x \bigg |_0^2 = \frac{x^4}{4} \bigg |_0^2 + x^2 \bigg |_0^2 + 2x \bigg |_0^2 \)

Далее следует подставить пределы интегрирования в каждую функцию и записать ответ:

\(\int_0^2 x^3dx + 2\int_0^2 xdx + 2\int_0^2 dx = \frac{x^4}{4} \bigg |_0^2 + 2 \frac{x^2}{2} \bigg |_0^2 + 2x \bigg |_0^2 = \frac{x^4}{4} \bigg |_0^2 + x^2 \bigg |_0^2 + 2x \bigg |_0^2 \)

Ответ: \(\int_0^2 (x^3 + 2x + 2) dx = 12\)

Задача 4

Необходимо найти решение интеграла:

\(\int 3\cos x dx\)

Решение

Требуется вынести константу по первому свойству за знак интеграла и записать ответ:

\(\int 3\cos x dx = 3 \int \cos x dx = 3 \sin x + C\)

Ответ: \(\int 3\cos x dx = 3 \sin x + C\)

Задача 5

Необходимо определить интеграл:

\(\int (e^x + \sin x) dx\)

Решение

Исходя из первого свойства неопределенного интеграла, интеграл суммы равен сумме интегралов:

\(\int (e^x + \sin x) dx = \int e^x dx + \int \sin x dx = e^x - \cos x\)

Ответ: \(\int (e^x + \sin x) dx = e^x - \cos x\)

Задача 6

Требуется определить производную от интеграла:

\( \int \ln x dx\)

Решение

Согласно третьему свойству неопределенного интеграла, производная неопределенного интеграла определяется, как подынтегральная функция:

\(\bigg (\int \ln x dx \bigg )' = \ln x\)

Ответ: \(\bigg (\int \ln x dx \bigg )' = \ln x\)

Задача 7

Требуется доказать следующее выражение:

\( \int (x^2+x)' = x^2+x+C\)

Решение

В первую очередь необходимо определить производную подынтегральной функции:

\( (x^2+x)' = (x^2)' + (x)' = 2x + 1\)

Исходя из первого и второго свойства неопределенного интеграла, получим ответ:

\(\int (2x+1) dx = \int 2x dx + \int 1 dx = 2 \int x dx + \int 1 dx =2 \cdot \frac{x^2}{2} + x + C = x^2 + x + C\)

Ответ: выражение доказано.

Благодаря теоретическим знаниям и практическим навыкам решения задач с интегралами, можно с легкостью осваивать самые сложные темы по физике и математическому анализу. Главное — уметь пользоваться таблицей с основными формулами и свойствами определенного и неопределенного интегралов. Если в процессе изучения материала возникают трудности, то в любое время можно открыть сервис Феникс.Хелп.